中考压轴题动点探究规律含详细答案

中考压轴题动点探究规律含详细答案

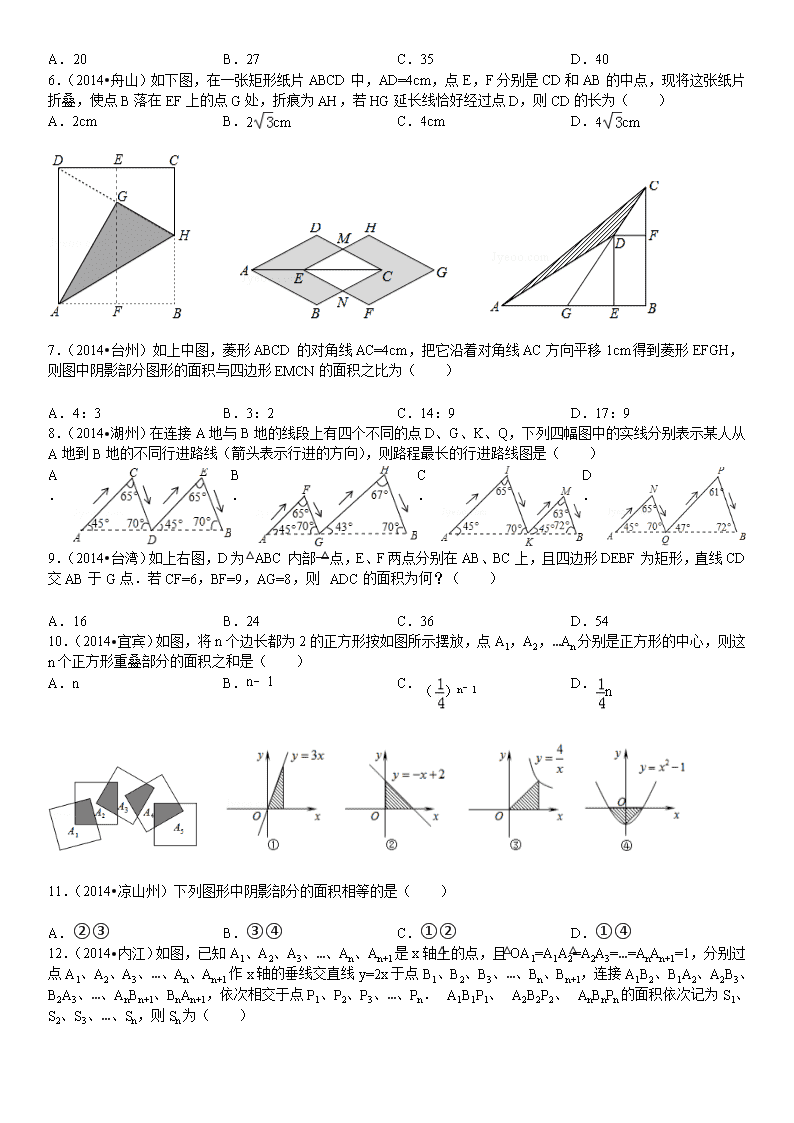
‎2015年05月22日规律&动点&选填 ‎ ‎　‎ 一．选择题（共12小题）‎ ‎1．（2014•绍兴）将一张正方形纸片，按如图步骤①，②，沿虚线对折两次，然后沿③中的虚线剪去一个角，展开铺平后的图形是（　　）‎ ‎　‎ A．‎ B．‎ C．‎ D．‎ ‎2．（2014•重庆）如图，△ABC的顶点A、B、C均在⊙O上，若∠ABC+∠AOC=90°，则∠AOC的大小是（　　）‎ A．‎ ‎30°‎ B．‎ ‎45°‎ C．‎ ‎60°‎ D．‎ ‎70°‎ ‎ ‎ ‎　‎ ‎3．（2014•重庆）下列图形都是按照一定规律组成，第一个图形中共有2个三角形，第二个图形中共有8个三角形，第三个图形中共有14个三角形，…，依此规律，第五个图形中三角形的个数是（　　）‎ ‎　‎ A．‎ ‎22‎ B．‎ ‎24‎ C．‎ ‎26‎ D．‎ ‎28‎ ‎4．（2014•重庆）如图，正方形ABCD的顶点B，C在x轴的正半轴上，反比例函数y=（k≠0）在第一象限的图象经过顶点A（m，2）和CD边上的点E（n，），过点E的直线l交x轴于点F，交y轴于点G（0，﹣2），则点F的坐标是（　　）‎ A．‎ ‎（，0）‎ B．‎ ‎（，0）‎ C．‎ ‎（，0）‎ D．‎ ‎（，0）‎ ‎ ‎ ‎　‎ ‎5．（2014•重庆）如图，下列图形都是由面积为1的正方形按一定的规律组成，其中，第（1）个图形中面积为1的正方形有2个，第（2）个图形中面积为1的正方形有5个，第（3）个图形中面积为1的正方形有9个，…，按此规律．则第（6）个图形中面积为1的正方形的个数为（　　）‎ ‎　‎ A．‎ ‎20‎ B．‎ ‎27‎ C．‎ ‎35‎ D．‎ ‎40‎ ‎6．（2014•舟山）如下图，在一张矩形纸片ABCD中，AD=4cm，点E，F分别是CD和AB的中点，现将这张纸片折叠，使点B落在EF上的点G处，折痕为AH，若HG延长线恰好经过点D，则CD的长为（　　）‎ A．‎ ‎2cm B．‎ ‎2cm C．‎ ‎4cm D．‎ ‎4cm ‎ ‎ ‎　‎ ‎7．（2014•台州）如上中图，菱形ABCD的对角线AC=4cm，把它沿着对角线AC方向平移1cm得到菱形EFGH，则图中阴影部分图形的面积与四边形EMCN的面积之比为（　　）‎ ‎　‎ A．‎ ‎4：3‎ B．‎ ‎3：2‎ C．‎ ‎14：9‎ D．‎ ‎17：9‎ ‎8．（2014•湖州）在连接A地与B地的线段上有四个不同的点D、G、K、Q，下列四幅图中的实线分别表示某人从A地到B地的不同行进路线（箭头表示行进的方向），则路程最长的行进路线图是（　　）‎ ‎　‎ A．‎ B．‎ C．‎ D．‎ ‎9．（2014•台湾）如上右图，D为△ABC内部一点，E、F两点分别在AB、BC上，且四边形DEBF为矩形，直线CD交AB于G点．若CF=6，BF=9，AG=8，则△ADC的面积为何？（　　）‎ ‎　‎ A．‎ ‎16‎ B．‎ ‎24‎ C．‎ ‎36‎ D．‎ ‎54‎ ‎10．（2014•宜宾）如图，将n个边长都为2的正方形按如图所示摆放，点A1，A2，…An分别是正方形的中心，则这n个正方形重叠部分的面积之和是（　　）‎ A．‎ n B．‎ n﹣1‎ C．‎ ‎（）n﹣1‎ D．‎ n ‎ ‎ ‎　‎ ‎11．（2014•凉山州）下列图形中阴影部分的面积相等的是（　　）‎ ‎　‎ A．‎ ‎②③‎ B．‎ ‎③④‎ C．‎ ‎①②‎ D．‎ ‎①④‎ ‎12．（2014•内江）如图，已知A1、A2、A3、…、An、An+1是x轴上的点，且OA1=A1A2=A2A3=…=AnAn+1=1，分别过点A1、A2、A3、…、An、An+1作x轴的垂线交直线y=2x于点B1、B2、B3、…、Bn、Bn+1，连接A1B2、B1A2、A2B3、B2A3、…、AnBn+1、BnAn+1，依次相交于点P1、P2、P3、…、Pn．△A1B1P1、△A2B2P2、△AnBnPn的面积依次记为S1、S2、S3、…、Sn，则Sn为（　　）‎ A．‎ B．‎ C．‎ D．‎ ‎　‎ ‎　‎ 二．填空题（共4小题）‎ ‎14．（2014•重庆）在一个不透明的盒子里装着4个分别标有数字1，2，3，4的小球，它们除数字不同外其余完全相同，搅匀后从盒子里随机取出1个小球，将小球上的数字作为a的值，则使关于x的不等式组只有一个整数解的概率为　　　　　　．‎ ‎15．（2014•台州）有一个计算程序，每次运算都是把一个数先乘以2，再除以它与1的和，多次重复进行这种运算的过程如下：‎ 则第n次运算的结果yn=　　　　　　（用含字母x和n的代数式表示）．‎ ‎16．（2014•宜宾）规定：sin（﹣x）=﹣sinx，cos（﹣x）=cosx，sin（x+y）=sinx•cosy+cosx•siny．‎ 据此判断下列等式成立的是　　　　　　（写出所有正确的序号）‎ ‎①cos（﹣60°）=﹣；‎ ‎②sin75°=；‎ ‎③sin2x=2sinx•cosx；‎ ‎④sin（x﹣y）=sinx•cosy﹣cosx•siny．‎ ‎　‎ 三．解答题（共13小题）‎ ‎17．（2014•重庆）为丰富居民业余生活，某居民区组建筹委会，该筹委会动员居民自愿集资建立一个书刊阅览室．经预算，一共需要筹资30000元，其中一部分用于购买书桌、书架等设施，另一部分用于购买书刊．‎ ‎（1）筹委会计划，购买书刊的资金不少于购买书桌、书架等设施资金的3倍，问最多用多少资金购买书桌、书架等设施？‎ ‎（2）经初步统计，有200户居民自愿参与集资，那么平均每户需集资150元．镇政府了解情况后，赠送了一批阅览室设施和书籍，这样，只需参与户共集资20000元．经筹委会进一步宣传，自愿参与的户数在200户的基础上增加了a%（其中a＞0）．则每户平均集资的资金在150元的基础上减少了a%，求a的值．‎ ‎18．（2014•新疆）如图1所示，在A，B两地之间有汽车站C站，客车由A地驶往C站，货车由B地驶往A地．两车同时出发，匀速行驶．图2是客车、货车离C站的路程y1，y2（千米）与行驶时间x（小时）之间的函数关系图象．‎ ‎（1）填空：A，B两地相距　　　　　　千米；‎ ‎（2）求两小时后，货车离C站的路程y2与行驶时间x之间的函数关系式；‎ ‎（3）客、货两车何时相遇？‎ ‎19．（2014•舟山）实验数据显示，一般成人喝半斤低度白酒后，1.5小时内其血液中酒精含量y（毫克/百毫升）与时间x（时）的关系可近似地用二次函数y=﹣200x2+400x刻画；1.5小时后（包括1.5小时）y与x可近似地用反比例函数y=（k＞0）刻画（如图所示）．‎ ‎（1）根据上述数学模型计算：‎ ‎①喝酒后几时血液中的酒精含量达到最大值？最大值为多少？‎ ‎②当x=5时，y=45，求k的值．‎ ‎（2）按国家规定，车辆驾驶人员血液中的酒精含量大于或等于20毫克/百毫升时属于“酒后驾驶”，不能驾车上路．参照上述数学模型，假设某驾驶员晚上20：00在家喝完半斤低度白酒，第二天早上7：00能否驾车去上班？请说明理由．‎ ‎20．（2014•台州）如图，某翼装飞行员从离水平地面高AC=500m的A处出发，沿着俯角为15°的方向，直线滑行1600米到达D点，然后打开降落伞以75°的俯角降落到地面上的B点．求他飞行的水平距离BC（结果精确到1m）．‎ ‎21．（2014•宁波）用正方形硬纸板做三棱柱盒子，每个盒子由3个矩形侧面和2个正三角形底面组成，硬纸板以如图两种方法裁剪（裁剪后边角料不再利用）．‎ A方法：剪6个侧面； B方法：剪4个侧面和5个底面．‎ 现有19张硬纸板，裁剪时x张用A方法，其余用B方法．‎ ‎（1）用x的代数式分别表示裁剪出的侧面和底面的个数；‎ ‎（2）若裁剪出的侧面和底面恰好全部用完，问能做多少个盒子？‎ ‎22．（2014•新疆）如图，直线y=﹣x+8与x轴交于A点，与y轴交于B点，动点P从A点出发，以每秒2个单位的速度沿AO方向向点O匀速运动，同时动点Q从B点出发，以每秒1个单位的速度沿BA方向向点A匀速运动，当一个点停止运动，另一个点也随之停止运动，连接PQ，设运动时间为t（s）（0＜t≤3）．‎ ‎（1）写出A，B两点的坐标；‎ ‎（2）设△AQP的面积为S，试求出S与t之间的函数关系式；并求出当t为何值时，△AQP的面积最大？‎ ‎（3）当t为何值时，以点A，P，Q为顶点的三角形与△ABO相似，并直接写出此时点Q的坐标．‎ ‎23．（2014•温州）如图，在平面直角坐标系中，点A，B的坐标分别为（﹣3，0），（0，6）．动点P从点O出发，沿x轴正方向以每秒1个单位的速度运动，同时动点C从点B出发，沿射线BO方向以每秒2个单位的速度运动，以CP，CO为邻边构造▱PCOD，在线段OP延长线上取点E，使PE=AO，设点P运动的时间为t秒．‎ ‎（1）当点C运动到线段OB的中点时，求t的值及点E的坐标；‎ ‎（2）当点C在线段OB上时，求证：四边形ADEC为平行四边形；‎ ‎（3）在线段PE上取点F，使PF=1，过点F作MN⊥PE，截取FM=2，FN=1，且点M，N分别在一，四象限，在运动过程中，设▱PCOD的面积为S．‎ ‎①当点M，N中有一点落在四边形ADEC的边上时，求出所有满足条件的t的值；‎ ‎②若点M，N中恰好只有一个点落在四边形ADEC的内部（不包括边界）时，直接写出S的取值范围．‎ ‎24．（2014•重庆）如图1，在▱ABCD中，AH⊥DC，垂足为H，AB=4，AD=7，AH=．现有两个动点E，F同时从点A出发，分别以每秒1个单位长度、每秒3个单位长度的速度沿射线AC方向匀速运动，在点E，F的运动过程中，以EF为边作等边△EFG，使△EFG与△ABC在射线AC的同侧，当点E运动到点C时，E，F两点同时停止运动，设运动时间为t秒．‎ ‎（1）求线段AC的长；‎ ‎（2）在整个运动过程中，设等边△EFG与△ABC重叠部分的面积为S，请直接写出S与t之间的函数关系式，并写出相应的自变量t的取值范围；‎ ‎（3）当等边△EFG的顶点E到达点C时，如图2，将△EFG绕着点C旋转一个角度α（0°＜α＜360°），在旋转过程中，点E与点C重合，F的对应点为F′，G的对应点为G′，设直线F′G′与射线DC、射线AC分别相交于M，N两点．试问：是否存在点M，N，使得△CMN是以∠MCN为底角的等腰三角形？若存在，请求出CM的长度；若不存在，请说明理由．‎ ‎25．（2014•温州）勾股定理神秘而美妙，它的证法多样，其巧妙各有不同，其中的“面积法”给了小聪以灵感，他惊喜地发现，当两个全等的直角三角形如图1或图2摆放时，都可以用“面积法”来证明，下面是小聪利用图1证明勾股定理的过程：‎ 将两个全等的直角三角形按图1所示摆放，其中∠DAB=90°，求证：a2+b2=c2．‎ 证明：连结DB，过点D作BC边上的高DF，则DF=EC=b﹣a．‎ ‎∵S四边形ADCB=S△ACD+S△ABC=b2+ab．‎ 又∵S四边形ADCB=S△ADB+S△DCB=c2+a（b﹣a）‎ ‎∴b2+ab=c2+a（b﹣a）‎ ‎∴a2+b2=c2‎ 请参照上述证法，利用图2完成下面的证明．‎ 将两个全等的直角三角形按图2所示摆放，其中∠DAB=90°．‎ 求证：a2+b2=c2‎ 证明：连结　　　　　　‎ ‎∵S五边形ACBED=　　　　　　‎ 又∵S五边形ACBED=　　　　　　‎ ‎∴　　　　　　‎ ‎∴a2+b2=c2．‎ ‎26．（2014•宁波）课本的作业题中有这样一道题：把一张顶角为36°的等腰三角形纸片剪两刀，分成3张小纸片，使每张小纸片都是等腰三角形，你能办到吗？请画示意图说明剪法．‎ 我们有多少种剪法，图1是其中的一种方法：‎ 定义：如果两条线段将一个三角形分成3个等腰三角形，我们把这两条线段叫做这个三角形的三分线．‎ ‎（1）请你在图2中用两种不同的方法画出顶角为45°的等腰三角形的三分线，并标注每个等腰三角形顶角的度数；（若两种方法分得的三角形成3对全等三角形，则视为同一种）‎ ‎（2）△ABC中，∠B=30°，AD和DE是△ABC的三分线，点D在BC边上，点E在AC边上，且AD=BD，DE=CE，设∠C=x°，试画出示意图，并求出x所有可能的值；‎ ‎（3）如图3，△ABC中，AC=2，BC=3，∠C=2∠B，请画出△ABC的三分线，并求出三分线的长．‎ ‎27．（2014•舟山）类比梯形的定义，我们定义：有一组对角相等而另一组对角不相等的凸四边形叫做“等对角四边形”．‎ ‎（1）已知：如图1，四边形ABCD是“等对角四边形”，∠A≠∠C，∠A=70°，∠B=80°．求∠C，∠D的度数．‎ ‎（2）在探究“等对角四边形”性质时：‎ ‎①小红画了一个“等对角四边形”ABCD（如图2），其中∠ABC=∠ADC，AB=AD，此时她发现CB=CD成立．请你证明此结论；‎ ‎②由此小红猜想：“对于任意‘等对角四边形’，当一组邻边相等时，另一组邻边也相等”．你认为她的猜想正确吗？若正确，请证明；若不正确，请举出反例．‎ ‎（3）已知：在“等对角四边形”ABCD中，∠DAB=60°，∠ABC=90°，AB=5，AD=4．求对角线AC的长．‎ ‎28．（2014•内江）如图，在△ABC中，D是BC边上的点（不与点B、C重合），连结AD．‎ 问题引入：‎ ‎（1）如图①，当点D是BC边上的中点时，S△ABD：S△ABC=　　　　　　；当点D是BC边上任意一点时，S△ABD：S△ABC=　　　　　　（用图中已有线段表示）．‎ 探索研究：‎ ‎（2）如图②，在△ABC中，O点是线段AD上一点（不与点A、D重合），连结BO、CO，试猜想S△BOC与S△ABC之比应该等于图中哪两条线段之比，并说明理由．‎ 拓展应用：‎ ‎（3）如图③，O是线段AD上一点（不与点A、D重合），连结BO并延长交AC于点F，连结CO并延长交AB于点E，试猜想++的值，并说明理由．‎ ‎29．（2014•凉山州）实验与探究：‎ 三角点阵前n行的点数计算 如图是一个三角点阵，从上向下数有无数多行，其中第一行有1个点，第二行有2个点…第n行有n个点…‎ 容易发现，10是三角点阵中前4行的点数的和，你能发现300是前多少行的点数的和吗？‎ 如果要用试验的方法，由上而下地逐行的相加其点数，虽然你能发现1+2+3+4+…+23+24=300．得知300是前24行的点数的和，但是这样寻找答案需我们先探求三角点阵中前n行的点数的和与n的数量关系 前n行的点数的和是1+2+3+…+（n﹣2）+（n﹣1）+n，可以发现．‎ ‎2×[1+2+3+…+（n﹣2）+（n﹣1）+n]‎ ‎=[1+2+3+…+（n﹣2）+（n﹣1）+n]+[n+（n﹣1）+（n﹣2）+…3+2+1]‎ 把两个中括号中的第一项相加，第二项相加…第n项相加，上式等号的后边变形为这n个小括号都等于n+1，整个式子等于n（n+1），于是得到 ‎1+2+3+…+（n﹣2）+（n﹣1）+n=n（n+1）‎ 这就是说，三角点阵中前n项的点数的和是n（n+1）‎ 下列用一元二次方程解决上述问题 设三角点阵中前n行的点数的和为300，则有n（n+1）=300‎ 整理这个方程，得：n2+n﹣600=0‎ 解方程得：n1=24，n2=﹣25‎ 根据问题中未知数的意义确定n=24，即三角点阵中前24行的点数的和是300．‎ 请你根据上述材料回答下列问题：‎ ‎（1）三角点阵中前n行的点数的和能是600吗？如果能，求出n；如果不能，试用一元二次方程说明道理．‎ ‎（2）如果把图中的三角点阵中各行的点数依次换成2、4、6、…、2n、…，你能探究出前n行的点数的和满足什么规律吗？这个三角点阵中前n行的点数的和能是600吗？如果能，求出n；如果不能，试用一元二次方程说明道理．‎ ‎　‎ ‎2015年05月22日规律&动点&选填 ‎ 参考答案与试题解析 ‎　‎ 一．选择题（共12小题）‎ ‎1．（2014•绍兴）将一张正方形纸片，按如图步骤①，②，沿虚线对折两次，然后沿③中的虚线剪去一个角，展开铺平后的图形是（　　）‎ ‎　‎ A．‎ B．‎ C．‎ D．‎ 解答：‎ 解：由题意要求知，展开铺平后的图形是B．‎ 故选：B．‎ ‎2．（2014•重庆）如图，△ABC的顶点A、B、C均在⊙O上，若∠ABC+∠AOC=90°，则∠AOC的大小是（　　）‎ ‎　‎ A．‎ ‎30°‎ B．‎ ‎45°‎ C．‎ ‎60°‎ D．‎ ‎70°‎ 分析：‎ 先根据圆周角定理得到∠ABC=∠AOC，由于∠ABC+∠AOC=90°，所以∠AOC+∠AOC=90°，然后解方程即可．故选：C．‎ ‎　‎ ‎3．（2014•重庆）下列图形都是按照一定规律组成，第一个图形中共有2个三角形，第二个图形中共有8个三角形，第三个图形中共有14个三角形，…，依此规律，第五个图形中三角形的个数是（　　）‎ ‎　‎ A．‎ ‎22‎ B．‎ ‎24‎ C．‎ ‎26‎ D．‎ ‎28‎ 解答：‎ 解：第一个图形有2+6×0=2个三角形；‎ 第二个图形有2+6×1=8个三角形；‎ 第三个图形有2+6×2=14个三角形；‎ ‎…‎ 第五个图形有2+6×4=26个三角形；‎ 故选：C．‎ ‎　‎ ‎4．（2014•重庆）如图，正方形ABCD的顶点B，C在x轴的正半轴上，反比例函数y=（k≠0）在第一象限的图象经过顶点A（m，2）和CD边上的点E（n，），过点E的直线l交x轴于点F，交y轴于点G（0，﹣2），则点F的坐标是（　　）‎ ‎　‎ A．‎ ‎（，0）‎ B．‎ ‎（，0）‎ C．‎ ‎（，0）‎ D．‎ ‎（，0）‎ 分析：‎ 由A（m，2）得到正方形的边长为2，则BC=2，所以n=2+m，根据反比例函数图象上点的坐标特征得到k=2•m=（2+m），解得m=1，则E点坐标为（3，），然后利用待定系数法确定直线GF的解析式为y=x﹣2，再求y=0时对应自变量的值，从而得到点F的坐标．‎ 解答：‎ 解：∵正方形的顶点A（m，2），‎ ‎∴正方形的边长为2，‎ ‎∴BC=2，‎ 而点E（n，），‎ ‎∴n=2+m，即E点坐标为（2+m，），‎ ‎∴k=2•m=（2+m），解得m=1，‎ ‎∴E点坐标为（3，），‎ 设直线GF的解析式为y=ax+b，‎ 把E（3，），G（0，﹣2）代入得，解得，‎ ‎∴直线GF的解析式为y=x﹣2，‎ 当y=0时，x﹣2=0，解得x=，‎ ‎∴点F的坐标为（，0）．‎ 故选：C．‎ ‎　‎ ‎5．（2014•重庆）如图，下列图形都是由面积为1的正方形按一定的规律组成，其中，第（1）个图形中面积为1的正方形有2个，第（2）个图形中面积为1的正方形有5个，第（3）个图形中面积为1的正方形有9个，…，按此规律．则第（6）个图形中面积为1的正方形的个数为（　　）‎ ‎　‎ A．‎ ‎20‎ B．‎ ‎27‎ C．‎ ‎35‎ D．‎ ‎40‎ 分析：‎ 第（1）个图形中面积为1的正方形有2个，第（2）个图形中面积为1的图象有2+3=5个，第（3）个图形中面积为1的正方形有2+3+4=9个，…，按此规律，第n个图形中面积为1的正方形有2+3+4+…+n+1=，进一步求得第（6）个图形中面积为1的正方形的个数即可．‎ 解答：‎ 解：第（1）个图形中面积为1的正方形有2个，‎ 第（2）个图形中面积为1的图象有2+3=5个，‎ 第（3）个图形中面积为1的正方形有2+3+4=9个，‎ ‎…，‎ 按此规律，‎ 第n个图形中面积为1的正方形有2+3+4+…+（n+1）=个，‎ 则第（6）个图形中面积为1的正方形的个数为2+3+4+5+6+7=27个．‎ 故选：B．‎ ‎　‎ ‎6．（2014•舟山）如图，在一张矩形纸片ABCD中，AD=4cm，点E，F分别是CD和AB的中点，现将这张纸片折叠，使点B落在EF上的点G处，折痕为AH，若HG延长线恰好经过点D，则CD的长为（　　）‎ ‎　‎ A．‎ ‎2cm B．‎ ‎2cm C．‎ ‎4cm D．‎ ‎4cm 分析：‎ 先证明EG是△DCH的中位线，继而得出DG=HG，然后证明△ADG≌△AHG，得出∠BAH=∠HAG=∠DAG=30°，在Rt△ABH中，可求出AB，也即是CD=AB=2 故选：B 点评：‎ 本题考查了翻折变换、三角形的中位线定理，解答本题的关键是判断出∠BAH=∠HAG=∠DAG=30°，注意熟练掌握翻折变换的性质．‎ ‎　‎ ‎7．（2014•台州）如图，菱形ABCD的对角线AC=4cm，把它沿着对角线AC方向平移1cm得到菱形EFGH，则图中阴影部分图形的面积与四边形EMCN的面积之比为（　　）‎ ‎　‎ A．‎ ‎4：3‎ B．‎ ‎3：2‎ C．‎ ‎14：9‎ D．‎ ‎17：9‎ 分析：‎ 首先得出△MEC∽△DAC，则=，进而得出=，即可得出答案．图中阴影部分图形的面积与四边形EMCN的面积之比为：=．‎ 故选：C．‎ ‎　‎ ‎8．（2014•湖州）在连接A地与B地的线段上有四个不同的点D、G、K、Q，下列四幅图中的实线分别表示某人从A地到B地的不同行进路线（箭头表示行进的方向），则路程最长的行进路线图是（　　）‎ ‎　‎ A．‎ B．‎ C．‎ D．‎ 分析：‎ 分别构造出平行四边形和三角形，根据平行四边形的性质和全等三角形的性质进行比较，即可判断．‎ 解答：‎ 解：A、延长AC、BE交于S，‎ ‎∵∠CAB=∠EDB=45°，‎ ‎∴AS∥ED，则SC∥DE．‎ 同理SE∥CD，‎ ‎∴四边形SCDE是平行四边形，‎ ‎∴SE=CD，DE=CS，‎ 即走的路线长是：AC+CD+DE+EB=AC+CS+SE+EB=AS+BS；‎ B、延长AF、BH交于S1，作FK∥GH与BH的延长线交于点K，‎ ‎∵∠SAB=∠S1AB=45°，∠SBA=∠S1BA=70°，AB=AB，‎ ‎∴△SAB≌△S1AB，‎ ‎∴AS=AS1，BS=BS1，‎ ‎∵∠FGH=180°﹣70°﹣43°=67°=∠GHB，‎ ‎∴FG∥KH，‎ ‎∵FK∥GH，‎ ‎∴四边形FGHK是平行四边形，‎ ‎∴FK=GH，FG=KH，‎ ‎∴AF+FG+GH+HB=AF+FK+KH+HB，‎ ‎∵FS1+S1K＞FK，‎ ‎∴AS+BS＞AF+FK+KH+HB，‎ 即AC+CD+DE+EB＞AF+FG+GH+HB，‎ C、D、同理可证得AI+IK+KM+MB＜AS2+BS2＜AN+NQ+QP+PB．‎ 综上所述，D选项的所走的线路最长．‎ 故选：D．‎ ‎　‎ ‎9．（2014•台湾）如图，D为△ABC内部一点，E、F两点分别在AB、BC上，且四边形DEBF为矩形，直线CD交AB于G点．若CF=6，BF=9，AG=8，则△ADC的面积为何？（　　）‎ ‎　‎ A．‎ ‎16‎ B．‎ ‎24‎ C．‎ ‎36‎ D．‎ ‎54‎ 解答：‎ 解：S△ADC=S△AGC﹣S△ADG ‎=×AG×BC﹣×AG×BF ‎=×8×（6+9）﹣×8×9‎ ‎=60﹣36‎ ‎=24． ‎ 故选：B．‎ ‎　‎ ‎10．（2014•宜宾）如图，将n个边长都为2的正方形按如图所示摆放，点A1，A2，…An分别是正方形的中心，则这n个正方形重叠部分的面积之和是（　　）‎ ‎　‎ A．‎ n B．‎ n﹣1‎ C．‎ ‎（）n﹣1‎ D．‎ n 解答：‎ 解：由题意可得一个阴影部分面积等于正方形面积的，即是×4=1，‎ ‎5个这样的正方形重叠部分（阴影部分）的面积和为：1×4，‎ n个这样的正方形重叠部分（阴影部分）的面积和为：1×（n﹣1）=n﹣1．‎ 故选：B．‎ ‎　‎ ‎11．（2014•凉山州）下列图形中阴影部分的面积相等的是（　　）‎ ‎　‎ A．‎ ‎②③‎ B．‎ ‎③④‎ C．‎ ‎①②‎ D．‎ ‎①④‎ 解答：‎ ‎②③的面积相等，故选：A．‎ ‎12．（2014•内江）如图，已知A1、A2、A3、…、An、An+1是x轴上的点，且OA1=A1A2=A2A3=…=AnAn+1=1，分别过点A1、A2、A3、…、An、An+1作x轴的垂线交直线y=2x于点B1、B2、B3、…、Bn、Bn+1，连接A1B2、B1A2、A2B3、B2A3、…、AnBn+1、BnAn+1，依次相交于点P1、P2、P3、…、Pn．△A1B1P1、△A2B2P2、△AnBnPn的面积依次记为S1、S2、S3、…、Sn，则Sn为（　　）‎ ‎　‎ A．‎ B．‎ C．‎ D．‎ 分析：‎ 根据图象上点的坐标性质得出点B1、B2、B3、…、Bn、Bn+1各点坐标，进而利用相似三角形的判定与性质得出S1、S2、S3、…、Sn，进而得出答案．‎ 解答：‎ 解：∵A1、A2、A3、…、An、An+1是x轴上的点，且OA1=A1A2=A2A3=…=AnAn+1=1，分别过点A1、A2、A3、…、An、An+1作x轴的垂线交直线y=2x于点B1、B2、B3、…、Bn、Bn+1，‎ ‎∴依题意得：B1（1，2），B2（2，4），B3（3，6），…，Bn（n，2n）‎ ‎∵A1B1∥A2B2，‎ ‎∴△A1B1P1∽△A2B2P1，‎ ‎∴=，‎ ‎∴△A1B1P1与△A2B2P1对应高的比为：1：2，‎ ‎∵A1A2=1，‎ ‎∴A1B1边上的高为：，‎ ‎∴=××2=，‎ 同理可得：=，=，‎ ‎∴Sn=．‎ 故选：D．‎ 二．填空题（共3小题）‎ ‎14．（2014•重庆）在一个不透明的盒子里装着4个分别标有数字1，2，3，4的小球，它们除数字不同外其余完全相同，搅匀后从盒子里随机取出1个小球，将小球上的数字作为a的值，则使关于x的不等式组只有一个整数解的概率为　　．‎ 解答：‎ 解：∵不等式组只有一个整数解，‎ ‎∴（a+2）﹣（2a﹣1）=1，‎ 解得a=2，‎ ‎∴P=．‎ 故答案为：．‎ ‎15．（2014•台州）有一个计算程序，每次运算都是把一个数先乘以2，再除以它与1的和，多次重复进行这种运算的过程如下：‎ 则第n次运算的结果yn=　　（用含字母x和n的代数式表示）．‎ 解答：‎ 解：将y1=代入得：y2==；将y2=代入得：y3==，‎ 依此类推，第n次运算的结果yn=．故答案为：．‎ ‎16．（2014•宜宾）规定：sin（﹣x）=﹣sinx，cos（﹣x）=cosx，sin（x+y）=sinx•cosy+cosx•siny．‎ 据此判断下列等式成立的是　②③④　（写出所有正确的序号）‎ ‎①cos（﹣60°）=﹣；②sin75°=；③sin2x=2sinx•cosx；④sin（x﹣y）=sinx•cosy﹣cosx•siny．‎ 解答：‎ 解：①cos（﹣60°）=cos60°=，命题错误；‎ ‎②sin75°=sin（30°+45°）=sin30°•cos45°+cos30°•sin45°=×+×=+=，命题正确；‎ ‎③sin2x=sinx•cosx+cosx•sinx=2sinx•cosx，命题正确；‎ ‎④sin（x﹣y）=sinx•cos（﹣y）+cosx•sin（﹣y）=sinx•cosy﹣cosx•siny，命题正确．‎ 故答案为：②③④．‎ 三．解答题（共13小题）‎ ‎17．（2014•重庆）为丰富居民业余生活，某居民区组建筹委会，该筹委会动员居民自愿集资建立一个书刊阅览室．经预算，一共需要筹资30000元，其中一部分用于购买书桌、书架等设施，另一部分用于购买书刊．‎ ‎（1）筹委会计划，购买书刊的资金不少于购买书桌、书架等设施资金的3倍，问最多用多少资金购买书桌、书架等设施？‎ ‎（2）经初步统计，有200户居民自愿参与集资，那么平均每户需集资150元．镇政府了解情况后，赠送了一批阅览室设施和书籍，这样，只需参与户共集资20000元．经筹委会进一步宣传，自愿参与的户数在200户的基础上增加了a%（其中a＞0）．则每户平均集资的资金在150元的基础上减少了a%，求a的值．‎ 解答：‎ 解：（1）设用于购买书桌、书架等设施的为x元，则购买书籍的有（30000﹣x）元，‎ 根据题意得：30000﹣x≥3x，‎ 解得：x≤7500．‎ 答：最多用7500元购买书桌、书架等设施；‎ ‎（2）根据题意得：200（1+a%）×150（1﹣a%）=20000‎ 整理得：a2+10a﹣3000=0，‎ 解得：a=50或a=﹣60（舍去），‎ 所以a的值是50．‎ ‎　‎ ‎18．（2014•新疆）如图1所示，在A，B两地之间有汽车站C站，客车由A地驶往C站，货车由B地驶往A地．两车同时出发，匀速行驶．图2是客车、货车离C站的路程y1，y2（千米）与行驶时间x（小时）之间的函数关系图象．‎ ‎（1）填空：A，B两地相距　440　千米；‎ ‎（2）求两小时后，货车离C站的路程y2与行驶时间x之间的函数关系式；‎ ‎（3）客、货两车何时相遇？‎ 解答：‎ 解：（1）填空：A，B两地相距：360+80=440千米；‎ ‎（2）由图可知货车的速度为80÷2=40千米/小时，‎ 货车到达A地一共需要2+360÷40=11小时，‎ 设y2=kx+b，代入点（2，0）、（11，360）得 ‎，‎ 解得，‎ 所以y2=40x﹣80；‎ ‎（3）设y1=mx+n，代入点（6，0）、（0，360）得 解得，‎ 所以y1=﹣60x+360‎ 由y1=y2得，40x﹣80=﹣60x+360‎ 解得x=4.4‎ 答：客、货两车经过4.4小时相遇．‎ ‎　‎ ‎19．（2014•舟山）实验数据显示，一般成人喝半斤低度白酒后，1.5小时内其血液中酒精含量y（毫克/百毫升）与时间x（时）的关系可近似地用二次函数y=﹣200x2+400x刻画；1.5小时后（包括1.5小时）y与x可近似地用反比例函数y=（k＞0）刻画（如图所示）．‎ ‎（1）根据上述数学模型计算：‎ ‎①喝酒后几时血液中的酒精含量达到最大值？最大值为多少？‎ ‎②当x=5时，y=45，求k的值．‎ ‎（2）按国家规定，车辆驾驶人员血液中的酒精含量大于或等于20毫克/百毫升时属于“酒后驾驶”，不能驾车上路．参照上述数学模型，假设某驾驶员晚上20：00在家喝完半斤低度白酒，第二天早上7：00能否驾车去上班？请说明理由．‎ 解答：‎ 解：（1）①y=﹣200x2+400x=﹣200（x﹣1）2+200，‎ ‎∴x=1时血液中的酒精含量达到最大值，最大值为200（毫克/百毫升）；‎ ‎②∵当x=5时，y=45，y=（k＞0），‎ ‎∴k=xy=45×5=225；‎ ‎（2）不能驾车上班；‎ 理由：∵晚上20：00到第二天早上7：00，一共有11小时，‎ ‎∴将x=11代入y=，则y=＞20，‎ ‎∴第二天早上7：00不能驾车去上班．‎ ‎20．（2014•台州）如图，某翼装飞行员从离水平地面高AC=500m的A处出发，沿着俯角为15°的方向，直线滑行1600米到达D点，然后打开降落伞以75°的俯角降落到地面上的B点．求他飞行的水平距离BC（结果精确到1m）．‎ 解答：‎ 解：过点D作DE⊥AC于点E，过点D作DF⊥BC于点F，‎ 由题意可得：∠ADE=15°，∠BDF=15°，AD=1600m，AC=500m，‎ ‎∴cos∠ADE=cos15°=≈0.97，∴≈0.97，‎ 解得：DE=1552（m），sin15°=≈0.26，∴≈0.26，解得；AE=416（m），‎ ‎∴DF=500﹣416=84（m），∴tan∠BDF=tan15°=≈0.27，∴≈0.27，‎ 解得：BF=22.68（m），‎ ‎∴BC=CF+BF=1552+22.68=1574.68≈1575（m），‎ 答：他飞行的水平距离为1575m．‎ ‎　‎ ‎21．（2014•宁波）用正方形硬纸板做三棱柱盒子，每个盒子由3个矩形侧面和2个正三角形底面组成，硬纸板以如图两种方法裁剪（裁剪后边角料不再利用）．‎ A方法：剪6个侧面； B方法：剪4个侧面和5个底面．‎ 现有19张硬纸板，裁剪时x张用A方法，其余用B方法．‎ ‎（1）用x的代数式分别表示裁剪出的侧面和底面的个数；‎ ‎（2）若裁剪出的侧面和底面恰好全部用完，问能做多少个盒子？‎ 分析：‎ ‎（1）由x张用A方法，就有（19﹣x）张用B方法，就可以分别表示出侧面个数和底面个数；‎ ‎（2）由侧面个数和底面个数比为3：2建立方程求出x的值，求出侧面的总数就可以求出结论．‎ 解答：‎ 解：（1）∵裁剪时x张用A方法，‎ ‎∴裁剪时（19﹣x）张用B方法．‎ ‎∴侧面的个数为：6x+4（19﹣x）=（2x+76）个，‎ 底面的个数为：5（19﹣x）=（95﹣5x）个；‎ ‎（2）由题意，得 ‎，‎ 解得：x=7，‎ 经检验，x=7是原分式方程的解，‎ ‎∴盒子的个数为：=30．‎ 答：裁剪出的侧面和底面恰好全部用完，能做30个盒子．‎ ‎　‎ ‎22．（2014•新疆）如图，直线y=﹣x+8与x轴交于A点，与y轴交于B点，动点P从A点出发，以每秒2个单位的速度沿AO方向向点O匀速运动，同时动点Q从B点出发，以每秒1个单位的速度沿BA方向向点A匀速运动，当一个点停止运动，另一个点也随之停止运动，连接PQ，设运动时间为t（s）（0＜t≤3）．‎ ‎（1）写出A，B两点的坐标；‎ ‎（2）设△AQP的面积为S，试求出S与t之间的函数关系式；并求出当t为何值时，△AQP的面积最大？‎ ‎（3）当t为何值时，以点A，P，Q为顶点的三角形与△ABO相似，并直接写出此时点Q的坐标．‎ 解答：‎ 解：（1）令y=0，则﹣x+8=0，‎ 解得x=6，‎ x=0时，y=y=8，‎ ‎∴OA=6，OB=8，‎ ‎∴点A（6，0），B（0，8）；‎ ‎（2）在Rt△AOB中，由勾股定理得，AB===10，‎ ‎∵点P的速度是每秒2个单位，点Q的速度是每秒1个单位，‎ ‎∴AP=2t，‎ AQ=AB﹣BQ=10﹣t，‎ ‎∴点Q到AP的距离为AQ•sin∠OAB=（10﹣t）×=（10﹣t），‎ ‎∴△AQP的面积S=×2t×（10﹣t）=﹣（t2﹣10t）=﹣（t﹣5）2+20，‎ ‎∵﹣＜0，0＜t≤3，‎ ‎∴当t=3时，△AQP的面积最大，S最大=﹣（3﹣5）2+20=；‎ ‎（3）若∠APQ=90°，则cos∠OAB=，‎ ‎∴=，‎ 解得t=，‎ 若∠AQP=90°，则cos∠OAB=，‎ ‎∴=，‎ 解得t=，‎ ‎∵0＜t≤3，‎ ‎∴t的值为，‎ 此时，OP=6﹣2×=，‎ PQ=AP•tan∠OAB=（2×）×=，‎ ‎∴点Q的坐标为（，），‎ 综上所述，t=秒时，以点A，P，Q为顶点的三角形与△ABO相似，此时点Q的坐标为（，）．‎ ‎　‎ ‎23．（2014•温州）如图，在平面直角坐标系中，点A，B的坐标分别为（﹣3，0），（0，6）．动点P从点O出发，沿x轴正方向以每秒1个单位的速度运动，同时动点C从点B出发，沿射线BO方向以每秒2个单位的速度运动，以CP，CO为邻边构造▱PCOD，在线段OP延长线上取点E，使PE=AO，设点P运动的时间为t秒．‎ ‎（1）当点C运动到线段OB的中点时，求t的值及点E的坐标；‎ ‎（2）当点C在线段OB上时，求证：四边形ADEC为平行四边形；‎ ‎（3）在线段PE上取点F，使PF=1，过点F作MN⊥PE，截取FM=2，FN=1，且点M，N分别在一，四象限，在运动过程中，设▱PCOD的面积为S．‎ ‎①当点M，N中有一点落在四边形ADEC的边上时，求出所有满足条件的t的值；‎ ‎②若点M，N中恰好只有一个点落在四边形ADEC的内部（不包括边界）时，直接写出S的取值范围．‎ 分析：‎ ‎（1）由C是OB的中点求出时间，再求出点E的坐标，‎ ‎（2）连接CD交OP于点G，由▱PCOD的对角线相等，求四边形ADEC是平行四边形．‎ ‎（3）当点C在BO上时，第一种情况，当点M在CE边上时，由△EMF∽△ECO求解，第二种情况，当点N在DE边上时，由△EFN∽△EPD求解；‎ 当点C在BO的延长线上时，第一种情况，当点M在DE边上时，由EMF∽△EDP求解，第二种情况，当点N在CE边上时，由△EFN∽△EOC求解；‎ ‎②当1≤t＜时和当＜t≤5时，分别求出S的取值范围，‎ 解答：‎ 解：（1）∵OB=6，C是OB的中点，‎ ‎∴BC=OB=3，‎ ‎∴2t=3即t=，‎ ‎∴OE=+3=，E（，0）；‎ ‎（2）如图，连接CD交OP于点G，‎ 在▱PCOD中，CG=DG，OG=PG，‎ ‎∵AO=PE，‎ ‎∴AG=EG，‎ ‎∴四边形ADEC是平行四边形．‎ ‎（3）①（Ⅰ）当点C在BO上时，‎ 第一种情况：如图，当点M在CE边上时，‎ ‎∵MF∥OC，‎ ‎∴△EMF∽△ECO，‎ ‎∴=，即=，‎ ‎∴t=1，‎ 第二种情况：当点N在DE边时，‎ ‎∵NF∥PD，‎ ‎∴△EFN∽△EPD，‎ ‎∴=，即=，‎ ‎∴t=，‎ ‎（Ⅱ）当点C在BO的延长线上时，‎ 第一种情况：当点M在DE边上时，‎ ‎∵MF∥PD，‎ ‎∴△EMF∽△EDP，‎ ‎∴= 即 =，‎ ‎∴t=，‎ 第二种情况：当点N在CE边上时，‎ ‎∵NF∥OC，‎ ‎∴△EFN∽△EOC，‎ ‎∴=即 =，‎ ‎∴t=5．‎ ‎②＜S≤或＜S≤20．‎ 当1≤t＜时，‎ S=t（6﹣2t）=﹣2（t﹣）2+，‎ ‎∵t=在1≤t＜范围内，‎ ‎∴＜S≤，‎ 当＜t≤5时，S=t（2t﹣6）=2（t﹣）2﹣，‎ ‎∴＜S≤20．‎ ‎　‎ ‎24．（2014•重庆）如图1，在▱ABCD中，AH⊥DC，垂足为H，AB=4，AD=7，AH=．现有两个动点E，F同时从点A出发，分别以每秒1个单位长度、每秒3个单位长度的速度沿射线AC方向匀速运动，在点E，F 的运动过程中，以EF为边作等边△EFG，使△EFG与△ABC在射线AC的同侧，当点E运动到点C时，E，F两点同时停止运动，设运动时间为t秒．‎ ‎（1）求线段AC的长；‎ ‎（2）在整个运动过程中，设等边△EFG与△ABC重叠部分的面积为S，请直接写出S与t之间的函数关系式，并写出相应的自变量t的取值范围；‎ ‎（3）当等边△EFG的顶点E到达点C时，如图2，将△EFG绕着点C旋转一个角度α（0°＜α＜360°），在旋转过程中，点E与点C重合，F的对应点为F′，G的对应点为G′，设直线F′G′与射线DC、射线AC分别相交于M，N两点．试问：是否存在点M，N，使得△CMN是以∠MCN为底角的等腰三角形？若存在，请求出CM的长度；若不存在，请说明理由．‎ 分析：‎ ‎（1）利用平行四边形性质、勾股定理，求出DH、CH的长度，可以判定△ACD为等腰三角形，则AC=AD=7；‎ ‎（2）首先证明点G始终在直线AB上，然后分析运动过程，求出不同时间段内S的表达式：‎ ‎①当0≤t≤时，如答图2﹣1所示，等边△EFG在△内部；‎ ‎②当＜t≤4时，如答图2﹣2所示，点G在线段AB上，点F在AC的延长线上；‎ ‎③当4＜t≤7时，如答图2﹣3所示，点G、F分别在AB、AC的延长线上，点E在线段AC上．‎ ‎（3）因为∠MCN为等腰三角形的底角，因此只可能有两种情形：‎ ‎①若点N为等腰三角形的顶点，如答图3﹣1所示；‎ ‎②若点M为等腰三角形的顶点，如答图3﹣2所示．‎ 解答：‎ 解：（1）∵▱ABCD，∴CD=AB=4．‎ 在Rt△ADH中，由勾股定理得：DH===2，‎ ‎∴CH=DH．‎ ‎∴AC=AD=7．‎ ‎（2）在运动过程中，AE=t，AF=3t，∴等边△EFG的边长EF=EG=GF=2t．‎ 如答图1，过点G作GP⊥AC于点P，则EP=EG=t，GP=EG=t．‎ ‎∴AP=AE+EP=2t．‎ ‎∴tan∠GAC===．‎ ‎∵tan∠BAC=tan∠ACH===，‎ ‎∴tan∠GAC=tan∠BAC，‎ ‎∴点G始终在射线AB上．‎ 设∠BAC=∠ACH=θ，则sinθ==，cosθ==．‎ ‎①当0≤t≤时，如答图2﹣1所示，等边△EFG在△内部．‎ S=S△EFG=EF2=（2t）2=t2；‎ ‎②当＜t≤4时，如答图2﹣2所示，点G在线段AB上，点F在AC的延长线上．‎ 过点B作BQ⊥AF于点Q，则BQ=AB•sinθ=4×=4，AQ=AB•cosθ=4×=8．‎ ‎∴CQ=AQ﹣AC=8﹣7=1．‎ 设BC与GF交于点K，过点K作KP⊥AF于点P，‎ 设KP=x，则PF==x，‎ ‎∴CP=CF﹣PF=3t﹣7﹣x．‎ ‎∵PK∥BQ，‎ ‎∴，即，解得：x=（3t﹣7）．‎ ‎∴S=S△EFG﹣S△CFK=t2﹣（3t﹣7）•（3t﹣7）=﹣t2+t﹣；‎ ‎③当4＜t≤7时，如答图2﹣3所示，点G、F分别在AB、AC的延长线上，点E在线段AC上．‎ 过点B作BQ⊥AF于点Q，则BQ=AB•sinθ=4×=4，AQ=AB•cosθ=4×=8．‎ ‎∴CQ=AQ﹣AC=8﹣7=1．‎ 设BC与GF交于点K，过点K作KP⊥AF于点P，‎ 设KP=x，则EP==x，‎ ‎∴CP=EP﹣CE=x﹣（7﹣t）=x﹣7+t．‎ ‎∵PK∥BQ，‎ ‎∴，即，解得：x=（7﹣t）．‎ ‎∴S=S△CEK=（7﹣t）•（7﹣t）=t2﹣t+．‎ 综上所述，S与t之间的函数关系式为：‎ S=．‎ ‎（3）设∠ACH=θ，则tanθ===，cosθ==．‎ 当点E与点C重合时，t=7，∴等边△EFG的边长=2t=14．‎ 假设存在点M，N，使得△CMN是以∠MCN为底角的等腰三角形，‎ ‎①若点N为等腰三角形的顶点，如答图3﹣1所示，则∠NMC=∠MCN=θ．‎ 过点C作CP⊥F′M于点P，则CP=CF′=7．‎ ‎∴PM===14．‎ 设CN=MN=x，则PN=PM﹣MN=14﹣x．‎ 在Rt△CNP中，由勾股定理得：CP2+PN2=CN2，即：（7）2+（14﹣x）2=x2，‎ 解得：x=．‎ 过点N作NQ⊥CM于点Q，‎ ‎∴CM=2CQ=2CN•cosθ=2××=7；‎ ‎②若点M为等腰三角形的顶点，如答图3﹣2所示，则∠MNC=∠MCN=θ．‎ 过点C作CP⊥G′N于点P，则CP=CF′=7．‎ ‎∴PN===14．‎ 设CM=MN=x，则PM=PN﹣MN=14﹣x．‎ 在Rt△CMP中，由勾股定理得：CP2+PM2=CM2，即：（7）2+（14﹣x）2=x2，‎ ‎∴CM=x=．‎ 综上所述，存在点M，N，使得△CMN是以∠MCN为底角的等腰三角形，CM的长度为7或．‎ ‎　‎ ‎25．（2014•温州）勾股定理神秘而美妙，它的证法多样，其巧妙各有不同，其中的“面积法”给了小聪以灵感，他惊喜地发现，当两个全等的直角三角形如图1或图2摆放时，都可以用“面积法”来证明，下面是小聪利用图1证明勾股定理的过程：‎ 将两个全等的直角三角形按图1所示摆放，其中∠DAB=90°，求证：a2+b2=c2．‎ 证明：连结DB，过点D作BC边上的高DF，则DF=EC=b﹣a．‎ ‎∵S四边形ADCB=S△ACD+S△ABC=b2+ab．‎ 又∵S四边形ADCB=S△ADB+S△DCB=c2+a（b﹣a）‎ ‎∴b2+ab=c2+a（b﹣a）‎ ‎∴a2+b2=c2‎ 请参照上述证法，利用图2完成下面的证明．‎ 将两个全等的直角三角形按图2所示摆放，其中∠DAB=90°．‎ 求证：a2+b2=c2‎ 证明：连结　BD，过点B作DE边上的高BF，则BF=b﹣a，　‎ ‎∵S五边形ACBED=　S△ACB+S△ABE+S△ADE=ab+b2+ab，　‎ 又∵S五边形ACBED=　S△ACB+S△ABD+S△BDE=ab+c2+a（b﹣a），　‎ ‎∴　ab+b2+ab=ab+c2+a（b﹣a），　‎ ‎∴a2+b2=c2．‎ 解答：‎ 证明：连结BD，过点B作DE边上的高BF，则BF=b﹣a，‎ ‎∵S五边形ACBED=S△ACB+S△ABE+S△ADE=ab+b2+ab，‎ 又∵S五边形ACBED=S△ACB+S△ABD+S△BDE=ab+c2+a（b﹣a），‎ ‎∴ab+b2+ab=ab+c2+a（b﹣a），‎ ‎∴a2+b2=c2．‎ 点评：‎ 此题主要考查了勾股定理得证明，表示出五边形面积是解题关键．‎ ‎　‎ ‎26．（2014•宁波）课本的作业题中有这样一道题：把一张顶角为36°的等腰三角形纸片剪两刀，分成3张小纸片，使每张小纸片都是等腰三角形，你能办到吗？请画示意图说明剪法．‎ 我们有多少种剪法，图1是其中的一种方法：‎ 定义：如果两条线段将一个三角形分成3个等腰三角形，我们把这两条线段叫做这个三角形的三分线．‎ ‎（1）请你在图2中用两种不同的方法画出顶角为45°的等腰三角形的三分线，并标注每个等腰三角形顶角的度数；（若两种方法分得的三角形成3对全等三角形，则视为同一种）‎ ‎（2）△ABC中，∠B=30°，AD和DE是△ABC的三分线，点D在BC边上，点E在AC边上，且AD=BD，DE=CE，设∠C=x°，试画出示意图，并求出x所有可能的值；‎ ‎（3）如图3，△ABC中，AC=2，BC=3，∠C=2∠B，请画出△ABC的三分线，并求出三分线的长．‎ 分析：‎ ‎（1）45°自然想到等腰直角三角形，过底角一顶点作对边的高，发现形成一个等腰直角三角形和直角三角形．直角三角形斜边的中线可形成两个等腰三角形，则易得一种情况．第二种情形可以考虑题例中给出的方法，试着同样以一底角作为新等腰三角形的底角，则另一底脚被分为45°和22.5°，再以22.5°分别作为等腰三角形的底角或顶角，易得其中作为底角时所得的三个三角形恰都为等腰三角形．即又一三分线作法．‎ ‎（2）用量角器，直尺标准作30°角，而后确定一边为BA，一边为BC，根据题意可以先固定BA的长，而后可确定D点，再标准作图实验﹣﹣分别考虑AD为等腰三角形的腰或者底边，兼顾A、E、C在同一直线上，易得2种三角形ABC．根据图形易得x的值．‎ ‎（3）因为∠C=2∠B，作∠C的角平分线，则可得第一个等腰三角形．而后借用圆规，以边长画弧，根据交点，寻找是否存在三分线，易得如图4图形为三分线．则可根据外角等于内角之和及腰相等等情况列出等量关系，求解方程可知各线的长．‎ 解答：‎ 解：（1）如图2作图，‎ ‎（2）如图3 ①、②作△ABC．‎ ‎①当AD=AE时，‎ ‎∵2x+x=30+30，‎ ‎∴x=20．‎ ‎②当AD=DE时，‎ ‎∵30+30+2x+x=180，‎ ‎∴x=40．‎ 所以∠C的度数是20°或40°；‎ ‎（3）如图4，CD、AE就是所求的三分线．‎ 设∠B=α，则∠DCB=∠DCA=∠EAC=α，∠ADE=∠AED=2α，‎ 此时△AEC∽△BDC，△ACD∽△ABC，‎ 设AE=AD=x，BD=CD=y，‎ ‎∵△AEC∽△BDC，‎ ‎∴x：y=2：3，‎ ‎∵△ACD∽△ABC，‎ ‎∴2：x=（x+y）：2，‎ 所以联立得方程组，‎ 解得 ，‎ 即三分线长分别是和．‎ ‎　‎ ‎27．（2014•舟山）类比梯形的定义，我们定义：有一组对角相等而另一组对角不相等的凸四边形叫做“等对角四边形”．‎ ‎（1）已知：如图1，四边形ABCD是“等对角四边形”，∠A≠∠C，∠A=70°，∠B=80°．求∠C，∠D的度数．‎ ‎（2）在探究“等对角四边形”性质时：‎ ‎①小红画了一个“等对角四边形”ABCD（如图2），其中∠ABC=∠ADC，AB=AD，此时她发现CB=CD成立．请你证明此结论；‎ ‎②由此小红猜想：“对于任意‘等对角四边形’，当一组邻边相等时，另一组邻边也相等”．你认为她的猜想正确吗？若正确，请证明；若不正确，请举出反例．‎ ‎（3）已知：在“等对角四边形”ABCD中，∠DAB=60°，∠ABC=90°，AB=5，AD=4．求对角线AC的长．‎ 分析：‎ ‎（1）利用“等对角四边形”这个概念来计算．‎ ‎（2）①利用等边对等角和等角对等边来证明；‎ ‎②举例画图；‎ ‎（3）（Ⅰ）当∠ADC=∠ABC=90°时，延长AD，BC相交于点E，利用勾股定理求解；‎ ‎（Ⅱ）当∠BCD=∠DAB=60°时，过点D作DE⊥AB于点E，DF⊥BC于点F，求出线段利用勾股定理求解．‎ 解答：‎ 解：（1）如图1‎ ‎∵等对角四边形ABCD，∠A≠∠C，‎ ‎∴∠D=∠B=80°，‎ ‎∴∠C=360°﹣70°﹣80°﹣80°=130°；‎ ‎（2）①如图2，连接BD，‎ ‎∵AB=AD，‎ ‎∴∠ABD=∠ADB，‎ ‎∵∠ABC=∠ADC，‎ ‎∴∠ABC﹣∠ABD=∠ADC﹣∠ADB，‎ ‎∴∠CBD=∠CDB，‎ ‎∴CB=CD，‎ ‎②不正确，‎ 反例：如图3，∠A=∠C=90°，AB=AD，‎ 但CB≠CD，‎ ‎（3）（Ⅰ）如图4，当∠ADC=∠ABC=90°时，延长AD，BC相交于点E，‎ ‎∵∠ABC=90°，∠DAB=60°，AB=5，‎ ‎∴AE=10，‎ ‎∴DE=AE﹣AD=10﹣4=6，‎ ‎∵∠EDC=90°，∠E=30°，‎ ‎∴CD=2，‎ ‎∴AC===2‎ ‎（Ⅱ）如图5，当∠BCD=∠DAB=60°时，过点D作DE⊥AB于点E，DF⊥BC于点F，‎ ‎∵DE⊥AB，∠DAB=60°AD=4，‎ ‎∴AE=2，DE=2，‎ ‎∴BE=AB﹣AE=5﹣2=3，‎ ‎∵四边形BFDE是矩形，‎ ‎∴DF=BE=3，BF=DE=2，‎ ‎∵∠BCD=60°，‎ ‎∴CF=，‎ ‎∴BC=CF+BF=+2=3，‎ ‎∴AC===2．‎ ‎　‎ ‎28．（2014•内江）如图，在△ABC中，D是BC边上的点（不与点B、C重合），连结AD．‎ 问题引入：‎ ‎（1）如图①，当点D是BC边上的中点时，S△ABD：S△ABC=　1：2　；当点D是BC边上任意一点时，S△ABD：S△ABC=　BD：BC　（用图中已有线段表示）．‎ 探索研究：‎ ‎（2）如图②，在△ABC中，O点是线段AD上一点（不与点A、D重合），连结BO、CO，试猜想S△BOC与S△ABC之比应该等于图中哪两条线段之比，并说明理由．‎ 拓展应用：‎ ‎（3）如图③，O是线段AD上一点（不与点A、D重合），连结BO并延长交AC于点F，连结CO并延长交AB于点E，试猜想++的值，并说明理由．‎ 分析：‎ ‎（1）根据三角形的面积公式，两三角形等高时，可得两三角形底与面积的关系，可得答案；‎ ‎（2）根据三角形的面积公式，两三角形等底时，可得两三角形的高与面积的关系，可得答案；‎ ‎（3）根据三角形的面积公式，两三角形等底时，可得两三角形的高与面积的关系，再根据分式的加减，可得答案．‎ 解答：‎ 解：（1）如图①，当点D是BC边上的中点时，S△ABD：S△ABC=1：2；当点D是BC边上任意一点时，S△ABD：S△ABC=BD：BC，‎ 故答案为：1：2，BD：BC；‎ ‎（2）S△BOC：S△ABC=OD：AD，‎ 如图②作OE⊥BC与E，作AF⊥BC与F，‎ ‎∵OE∥AF，‎ ‎∴△OED∽△AFD，‎ ‎．‎ ‎∵，‎ ‎∴；‎ ‎（3）++=1，理由如下：‎ 由（2）得，，．‎ ‎∴++=++‎ ‎=‎ ‎=‎ ‎=1．‎ ‎　‎ ‎29．（2014•凉山州）实验与探究：‎ 三角点阵前n行的点数计算 如图是一个三角点阵，从上向下数有无数多行，其中第一行有1个点，第二行有2个点…第n行有n个点…‎ 容易发现，10是三角点阵中前4行的点数的和，你能发现300是前多少行的点数的和吗？‎ 如果要用试验的方法，由上而下地逐行的相加其点数，虽然你能发现1+2+3+4+…+23+24=300．得知300是前24行的点数的和，但是这样寻找答案需我们先探求三角点阵中前n行的点数的和与n的数量关系 前n行的点数的和是1+2+3+…+（n﹣2）+（n﹣1）+n，可以发现．‎ ‎2×[1+2+3+…+（n﹣2）+（n﹣1）+n]‎ ‎=[1+2+3+…+（n﹣2）+（n﹣1）+n]+[n+（n﹣1）+（n﹣2）+…3+2+1]‎ 把两个中括号中的第一项相加，第二项相加…第n项相加，上式等号的后边变形为这n个小括号都等于n+1，整个式子等于n（n+1），于是得到 ‎1+2+3+…+（n﹣2）+（n﹣1）+n=n（n+1）‎ 这就是说，三角点阵中前n项的点数的和是n（n+1）‎ 下列用一元二次方程解决上述问题 设三角点阵中前n行的点数的和为300，则有n（n+1）=300‎ 整理这个方程，得：n2+n﹣600=0‎ 解方程得：n1=24，n2=﹣25‎ 根据问题中未知数的意义确定n=24，即三角点阵中前24行的点数的和是300．‎ 请你根据上述材料回答下列问题：‎ ‎（1）三角点阵中前n行的点数的和能是600吗？如果能，求出n；如果不能，试用一元二次方程说明道理．‎ ‎（2）如果把图中的三角点阵中各行的点数依次换成2、4、6、…、2n、…，你能探究出前n行的点数的和满足什么规律吗？这个三角点阵中前n行的点数的和能是600吗？如果能，求出n；如果不能，试用一元二次方程说明道理．‎ 分析：‎ ‎（1）由于第一行有1个点，第二行有2个点…第n行有n个点…，则前n行共有（1+2+3+4+5+…+n ‎）个点，然后求它们的和，前n行共有个点，则=600，然后解方程得到n的值；‎ ‎（2）根据2+4+6+…+2n=2（1+2+3+…+n）=2×个进而得出规律；根据规律可得n（n+1）=600，求n的值即可．‎ 解答：‎ 解：（1）由题意可得：=600，‎ 整理得n2+n﹣1200=0，‎ 此方程无正整数解，‎ 所以，三角点阵中前n行的点数的和不可能是600；‎ ‎（2）由题意可得：‎ ‎2+4+6+…+2n=2（1+2+3+…+n）=2×=n（n+1）；‎ 依题意，得n（n+1）=600，‎ 整理得n2+n﹣600=0，‎ ‎（n+25）（n﹣24）=0，‎ ‎∴n1=﹣25，n2=24，‎ ‎∵n为正整数，‎ ‎∴n=24．‎ 故n的值是24．‎ ‎　‎