中考的最短路径问题

中考的最短路径问题

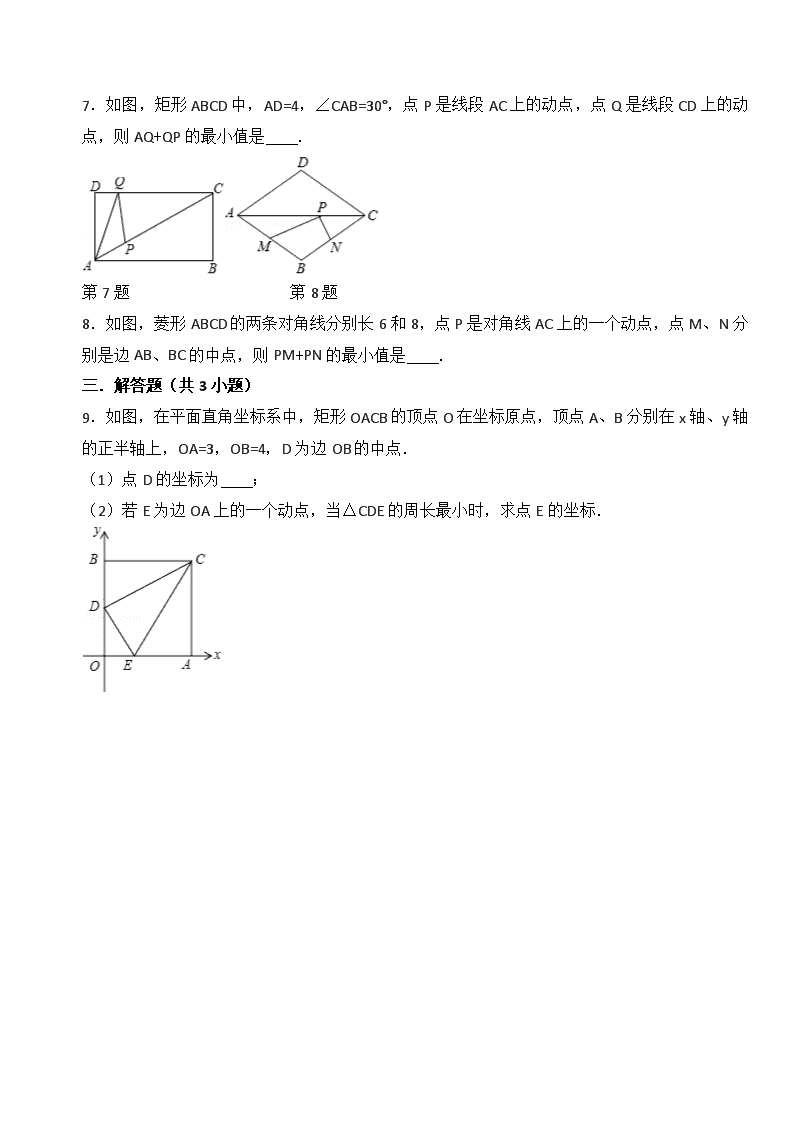
中考的最短路径问题　‎ 一．选择题（共5小题）‎ ‎1．如图，正方形ABCD的边长为8，点M在边DC上，且DM=2，点N是边AC上一动点，则线段DN+MN的最小值为（　　）‎ A．8 B．8 C．2 D．10‎ ‎ ‎ ‎ 第1题 第2题 第4题 第5题 ‎2．如图，在Rt△ABC中，∠ACB=90°，AC=6，BC=8，AD是∠BAC的平分线．若P，Q分别是AD和AC上的动点，则PC+PQ的最小值是（　　）‎ A．2.4 B．4 C．4.8 D．5‎ ‎3．平面直角坐标系xOy中，已知A（﹣1，0）、B（3，0）、C（0，﹣1）三点，D（1，m）是一个动点，当△ACD的周长最小时，△ABD的面积为（　　）‎ A． B． C． D．‎ ‎4．如图，在Rt△ABC中，CA=CB=2，M为CA的中点，在AB上存在一点P，连接PC、PM，则△PMC周长的最小值是（　　）‎ A． B． C．+1 D．+1‎ ‎5．如图，在平面直角坐标系中，已知点A（0，3），B（3，0），点C在线段AB上，且点C的横坐标为1．若点P为y轴上的一个动点，则PC+PB的最小值是（　　）‎ A．2 B．4 C．3 D．1+2‎ ‎　二．填空题（共3小题）‎ ‎6．如图，正方形ABCD的边长为8，O是BC的中点，点P是对角线AC上一动点，则PO+PB的最小值为　　．‎ ‎7．如图，矩形ABCD中，AD=4，∠CAB=30°，点P是线段AC上的动点，点Q是线段CD上的动点，则AQ+QP的最小值是　　．‎ 第7题 第8题 ‎8．如图，菱形ABCD的两条对角线分别长6和8，点P是对角线AC上的一个动点，点M、N分别是边AB、BC的中点，则PM+PN的最小值是　　．‎ 三．解答题（共3小题）‎ ‎9．如图，在平面直角坐标系中，矩形OACB的顶点O在坐标原点，顶点A、B分别在x轴、y轴的正半轴上，OA=3，OB=4，D为边OB的中点．‎ ‎（1）点D的坐标为　　；‎ ‎（2）若E为边OA上的一个动点，当△CDE的周长最小时，求点E的坐标．‎ ‎10．如图所示，在一笔直的公路MN的同一旁有两个新开发区A，B，已知AB=10千米，直线AB与公路MN的夹角∠AON=30°，新开发区B到公路MN的距离BC=3千米．‎ ‎（1）新开发区A到公路MN的距离为　　；‎ ‎（2）现要在MN上某点P处向新开发区A，B修两条公路PA，PB，使点P到新开发区A，B的距离之和最短．此时PA+PB=　　（千米）．‎ ‎11．如图，C为线段BD上一动点，分别过点B、D作AB⊥BD，ED⊥BD，连接AC、EC．已知AB=2，DE=1，BD=8，设CD=x．‎ ‎（1）用含x的代数式表示AC+CE的长；‎ ‎（2）请问点C满足什么条件时，AC+CE的值最小；‎ ‎（3）根据（2）中的规律和结论，请构图求出代数式的最小值．‎