2011年广东省河源市中考数学试题

2011年广东省河源市中考数学试题

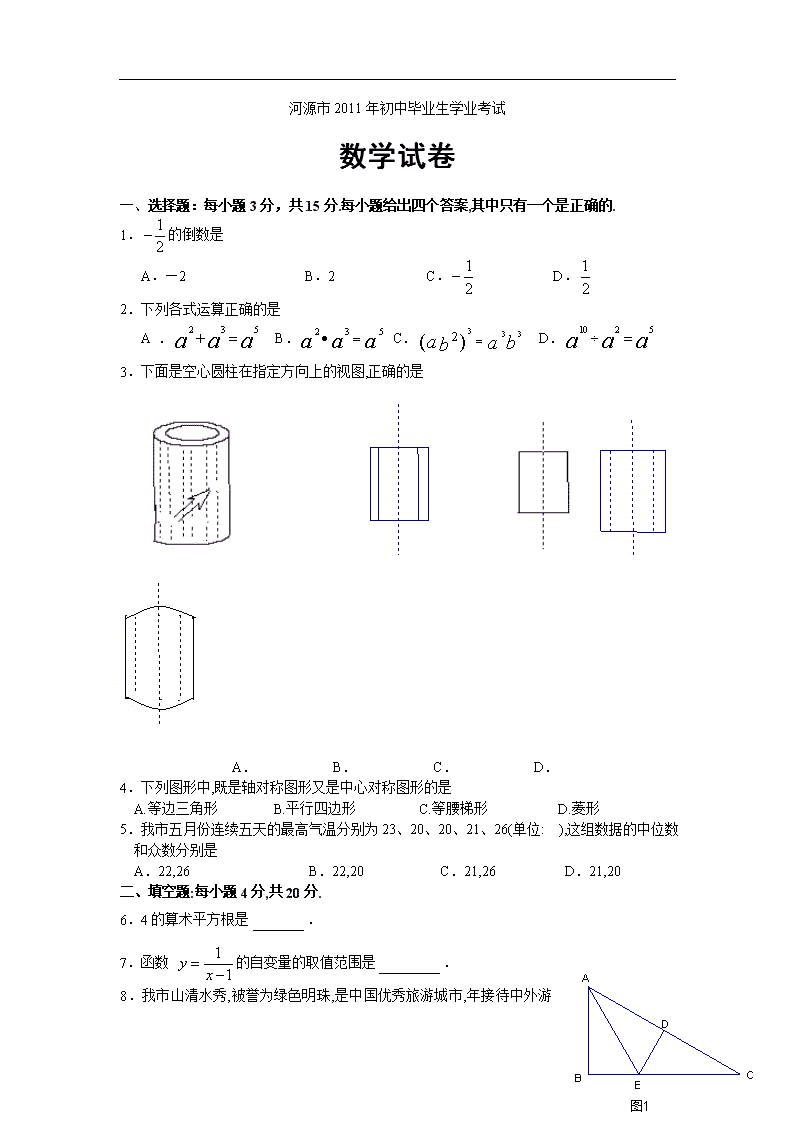
‎ 河源市2011年初中毕业生学业考试 数学试卷 一、选择题：每小题3分，共15分.每小题给出四个答案,其中只有一个是正确的.‎ ‎1．的倒数是 A．—2 B．‎2 C． D．‎ ‎2．下列各式运算正确的是 ‎ A ． B． C． D．‎ ‎3．下面是空心圆柱在指定方向上的视图,正确的是 ‎ ‎ ‎ A． B． C． D． ‎ ‎4．下列图形中,既是轴对称图形又是中心对称图形的是 ‎ A.等边三角形 B.平行四边形 C.等腰梯形 D.菱形 ‎5．我市五月份连续五天的最高气温分别为23、20、20、21、26(单位: ),这组数据的中位数 ‎ 和众数分别是 ‎ ‎ A．22,26 B．22,‎20 C．21,26 D．21,20‎ 二、填空题:每小题4分,共20分.‎ ‎6．4的算术平方根是．‎ ‎7．函数 的自变量的取值范围是．‎ ‎8．我市山清水秀,被誉为绿色明珠,是中国优秀旅游城市,年接待中外游客约5000000人,这个数字用科学记数法表示为人.‎ ‎9．如图1,在 Rt△ABC中,∠B=90°.ED是AC的垂直平分线,交AC于点D,交BC于点E,已知∠BAE=30°,则∠C的度数为°　　　　　　　　　　‎ ‎10．凸n边形的对角线的条数记作，例如：，那么：①；②；③‎ ‎．（，用含的代数式表示）　　　　　　　　‎ 三、解答题（一）（本大题5小题，每小题6分，共30分）‎ ‎11．（本题满分6分）‎ ‎ 计算：．‎ ‎12．（本题满分6分）‎ 化简：．‎ ‎13．（本题满分6分）‎ ‎ 某校九年级数学兴趣小组的同学开展了测量东江宽度的活动。如图2，他们在河东岸边的A点测得河西岸边的标志物B在它的正西方向，然后从A点出发沿河岸向正北方向行进‎200米到点C处，测得B在点C的南偏西60° 的方向上，他们测得东江的宽度是多少米？‎ ‎（结果保留整数，参考数据：‎ ‎14．（本题满分6分）‎ 王老师对河东中学九（一）班的某次模拟考试成绩进行统计后，绘制了频数分布直方图（如图3，分数取正整数，满分120分）．根据图形，回答下列问题：（直接填写结果）‎ ‎（1）该班有名学生；‎ ‎（2）89.5 --99.5这一组的频数是 ，频率是 ‎（3）估算该班这次数学模拟考试的平均成绩 是 ． ‎ ‎15．（本题满分6分）‎ ‎ 如图4，在平面直角坐标系中，点A（-4，4），点B（-4，0），将△ABO绕原点O按顺时针方向旋转135°得到△A B O。回答下列问题：（直接写结果）‎ ‎（1）∠AOB= °；‎ ‎（2）顶点A从开始到经过的路径长为 ；‎ ‎（3）点的坐标为 四、解答题（二）（本大题4小题，每小题7分，共28分）‎ ‎16．（本题满分7分)‎ ‎ 如图5，点P在平行四边形ABCD的CD边上，连结BP并延长与 AD的延长线交于点Q．‎ ‎ （1）求证：△DQP∽△CBP；‎ ‎ （2）当△DQP≌△CBP，且AB=8时，求DP的长．‎ ‎17．(本题满分7分)‎ ‎ 如图6,我市某展览厅东面有两个入口A、B,南面、西面、北面各有一个出口.小华任选择一个入口进入展览大厅,参观结束后任选一个出口离开．‎ ‎ (1)利用树状图表示她从进入到离开的所有路径；‎ ‎(2) 她从入口A进入展厅并从北出口离开的概率是多少? ‎ ‎18．(本题满分7分.)‎ ‎ 如图7,反比例函数的图像与一次函数的图象交于点A、B,其中A(1,2)．‎ ‎ (1)求m，b的值；‎ ‎ (2)求点B的坐标,并写出时，的取值范围． ‎ ‎ 图7 ‎ ‎19．(本题满分7分)‎ ‎ ‎ ‎ 为了鼓励城区居民节约用水,某市规定用水收费标准如下：每户每月的用水量不超过20度时(1度=‎1米),水费为a元/度；超过20度时，不超过部分仍为a元/度，超过部分为b元/度．已知某用户四份用水15度,交水费22.5元,五月份用水30度,交水费50元．‎ ‎ (1)求a,b的值；‎ ‎（2）若估计该用户六月份的水费支出不少于60元，但不超过90元，求该用户六月份的用水量x的取值范围．‎ 五、解答题(三)(本大题3小题,每小题9分,共27分)‎ ‎20．(本题满分9分) ‎ ‎ 如图8,等腰梯形ABCD中,AB∥CD,AD=BC.将△ACD沿对角线AC翻折后,点D恰好与边AB的中点M重合． ‎ ‎ (1)点C是否在以AB为直径的圆上?请说明理由; ‎ ‎ (2)当AB=4时,求此梯形的面积．‎ ‎21．(本题满分9分)‎ ‎ 如图9,已知线段AB的长为‎2a，点P是AB上的动点（P不与A，B重合），分别以AP、PB为边向线段AB的同一侧作正△APC和正△PBD．‎ ‎ （1）当△APC与△PBD的面积之生取最小值时，AP=；（直接写结果）‎ ‎ （2）连结AD、BC，相交于点Q，设∠AQC=α，那么α的大小是否会随点P的移动面变化？请说明理由；‎ ‎ （3）如图10，若点P固定，将△PBD绕点P按顺时针方向旋转（旋转角小于180°），此时α的大小是否发生变化？（只需直接写出你的猜想，不必证明）‎ ‎22．(本题满分9分)‎ ‎ 如图11，已知抛物线与x 轴交于两点A、B，其顶点为C． ‎ ‎(1)对于任意实数m，点M（m，-2）是否在该抛物线上?请说明理由；‎ ‎(2)求证:△ABC是等腰直角三角形；‎ ‎(3)已知点D在x轴上，那么在抛物线上是否存在点P，使得以B、C、D、P为顶点的四边形是平行四边形？若存在，求点P的坐标；若不存在，请说明理由．‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ 图11 ‎