- 2021-05-10 发布 |
- 37.5 KB |
- 5页

申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
中考数学整体思想练习
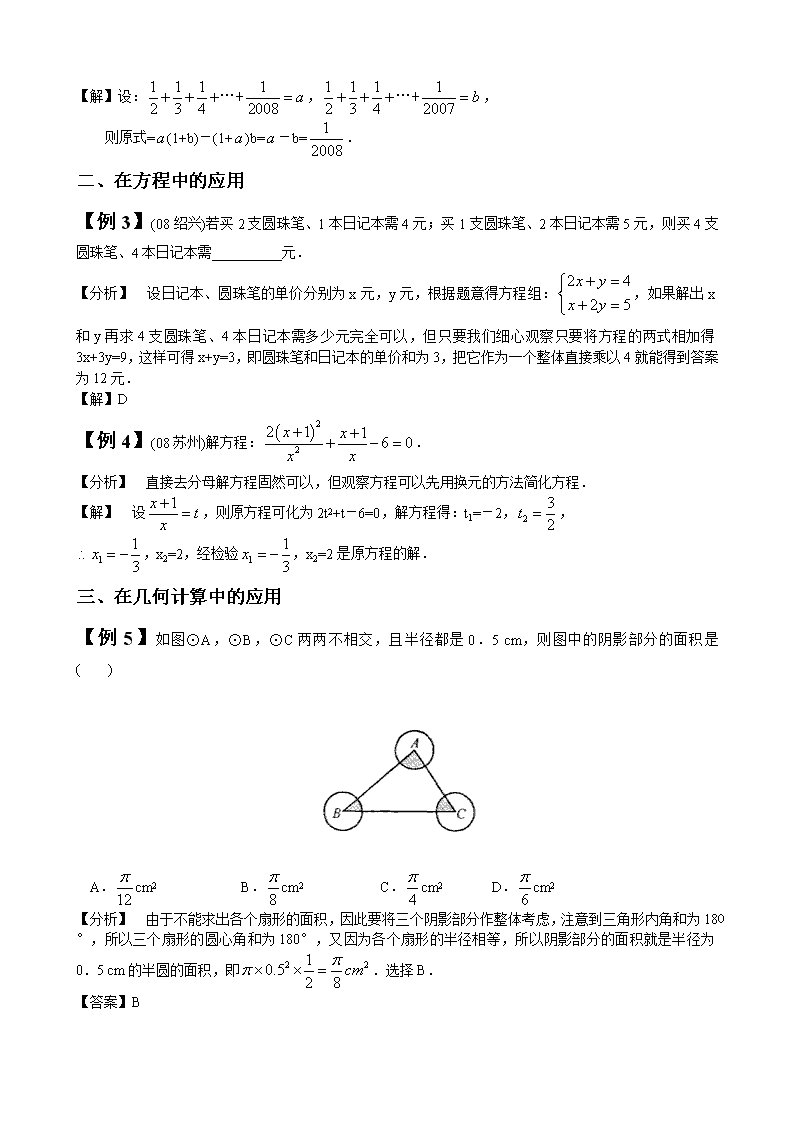
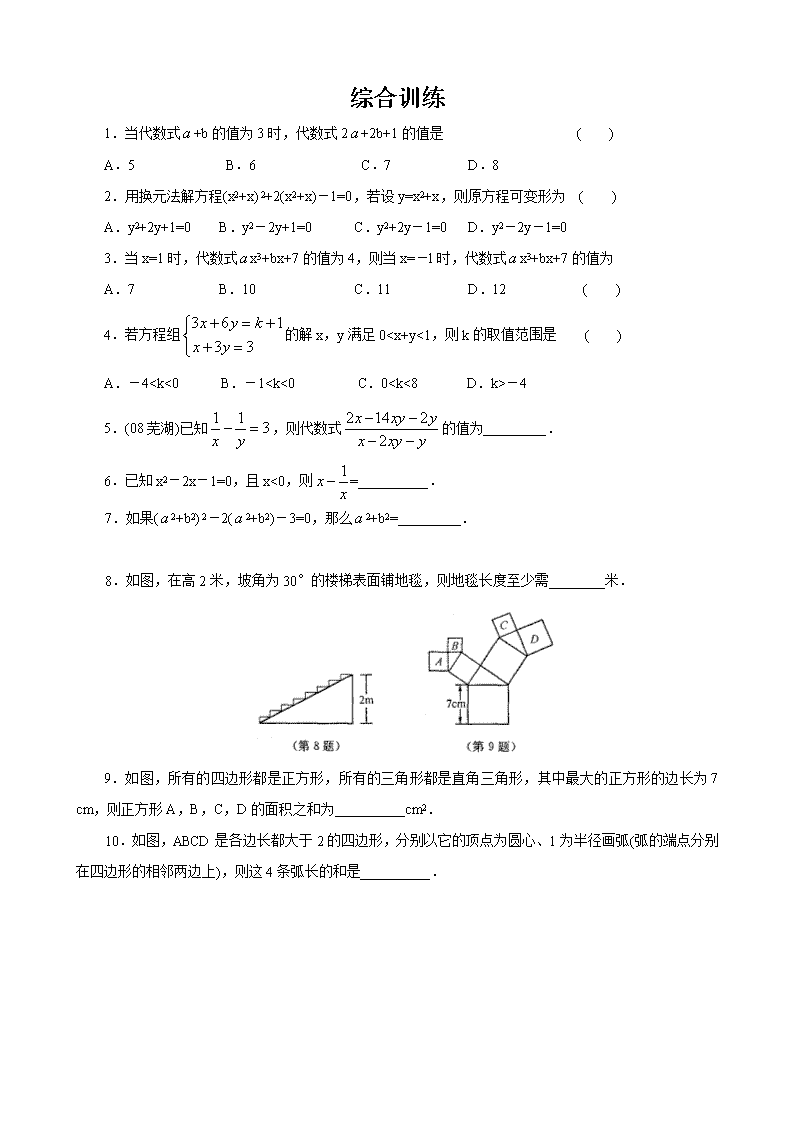
中考数学专项讲解 整体思想 知识梳理 整体思想就是在解决数学问题时,将要解决的问题看作一个整体,通过对问题的整体形式、整体结构、 已知条件和所求综合考虑后.得出结论.整体思想的应用,要做到观察全局、整体代入、整体换元、整体 构造.整体思想作为重要的数学思想之一,我们在解题过程中经常使用.整体思想使用得恰当,能提高解 题效率和能力,减少不必要的计算和走弯路,直奔主题.因而在处理数与式的运算、方程、几何计算等方 面有着广泛应用.是初中数学学习中的重要思想方法. 典型例题 一、在数与式的运算中的应用 【例 1】 已知代数式 3x2-4x+6 的值为 9,则 的值为 ( ) A.18 B.12 C.9 D.7 【分析】 如果根据题意直接求出 x 再代入到 中求值将非常麻烦,特别是 x 为一个无理数.考 虑到由题意 3x2-4x=3 成立,而 3x2-4x 是 的 3 倍,所以可以将 看作一个整体,则 . 【解】D 此题是灵活运用数学方法,解题技巧求值的问题,首先要观察一直条件和需要求解的代数式,然 后将已知条件变换成适合所求代数式的形式,运用主题带入法即可得解【练习】先化简,再求值 ,其中 满足 2-2 -1=0. 【分析】 对分式进行化筒结果为 ,如果把 求出具体值再代入计算会很麻烦,但如果把 2-2 看成一个整体,则由已知可得 2-2 =1,所以原式= . 【解】原式= 当 2-2 =1 时,原式= . 【例 2】计算: 【分析】 如果直接计算,运算量非常大,观察括号内的算式的特征.考虑用“整体替换”. 2 4 63x x− + 2 4 63x x− + 2 4 3x x− 2 4 3x x− 2 4 6 1 6 73x x− + = + = 2 2 2 1 4 2 4 4 2 a a a a a a a a + − − − ÷ − − + − a a a 2 1 2a a− a a a a a 2 1 12a a =− ( ) ( ) ( )2 2 2 2 1 4 4 2 1 2 2 4 22 2 a a a a a a a a a a aa a a + − − − −− ÷ = = − − − −− − a a 2 1 12a a =− 1 1 1 1 1 1 1 112 3 4 2008 2 3 4 2007 + + + + + + + + + − … … 1 1 1 1 1 1 1 11 2 3 4 2008 2 3 4 2007 + + + + + + + … + … + 【解】设: , , 则原式= (1+b)-(1+ )b= -b= . 二、在方程中的应用 【例 3】(08 绍兴)若买 2 支圆珠笔、1 本日记本需 4 元;买 1 支圆珠笔、2 本日记本需 5 元,则买 4 支 圆珠笔、4 本日记本需__________元. 【分析】 设日记本、圆珠笔的单价分别为 x 元,y 元,根据题意得方程组: ,如果解出 x 和 y 再求 4 支圆珠笔、4 本日记本需多少元完全可以,但只要我们细心观察只要将方程的两式相加得 3x+3y=9,这样可得 x+y=3,即圆珠笔和日记本的单价和为 3,把它作为一个整体直接乘以 4 就能得到答案 为 12 元. 【解】D 【例 4】(08 苏州)解方程: . 【分析】 直接去分母解方程固然可以,但观察方程可以先用换元的方法简化方程. 【解】 设 ,则原方程可化为 2t2+t-6=0,解方程得:t1=-2, , ,x2=2,经检验 ,x2=2 是原方程的解. 三、在几何计算中的应用 【例 5】如图⊙A,⊙B,⊙C 两两不相交,且半径都是 0.5 cm,则图中的阴影部分的面积是 ( ) A. cm2 B. cm2 C. cm2 D. cm2 【分析】 由于不能求出各个扇形的面积,因此要将三个阴影部分作整体考虑,注意到三角形内角和为 180 °,所以三个扇形的圆心角和为 180°,又因为各个扇形的半径相等,所以阴影部分的面积就是半径为 0.5 cm 的半圆的面积,即 .选择 B. 【答案】B 1 1 1 1 2 3 4 2008 a+ + + =… + 1 1 1 1 2 3 4 2007 b+ + + =… + a a a 1 2008 2 4 2 5 x y x y + = + = ( )2 2 2 1 1 6 0x x x x + ++ − = 1x tx + = 2 3 2t = 1 1 3x∴ = − 1 1 3x = − 12 π 8 π 4 π 6 π 2 210.5 2 8 cm ππ × × = 综合训练 1.当代数式 +b 的值为 3 时,代数式 2 +2b+1 的值是 ( ) A.5 B.6 C.7 D.8 2.用换元法解方程(x2+x) 2+2(x2+x)-1=0,若设 y=x2+x,则原方程可变形为 ( ) A.y2+2y+1=0 B.y2-2y+1=0 C.y2+2y-1=0 D.y2-2y-1=0 3.当 x=1 时,代数式 x3+bx+7 的值为 4,则当 x=-l 时,代数式 x3+bx+7 的值为 A.7 B.10 C.11 D.12 ( ) 4.若方程组 的解 x,y 满足 0查看更多