辽宁省本溪市中考数学试题及解析

辽宁省本溪市中考数学试题及解析

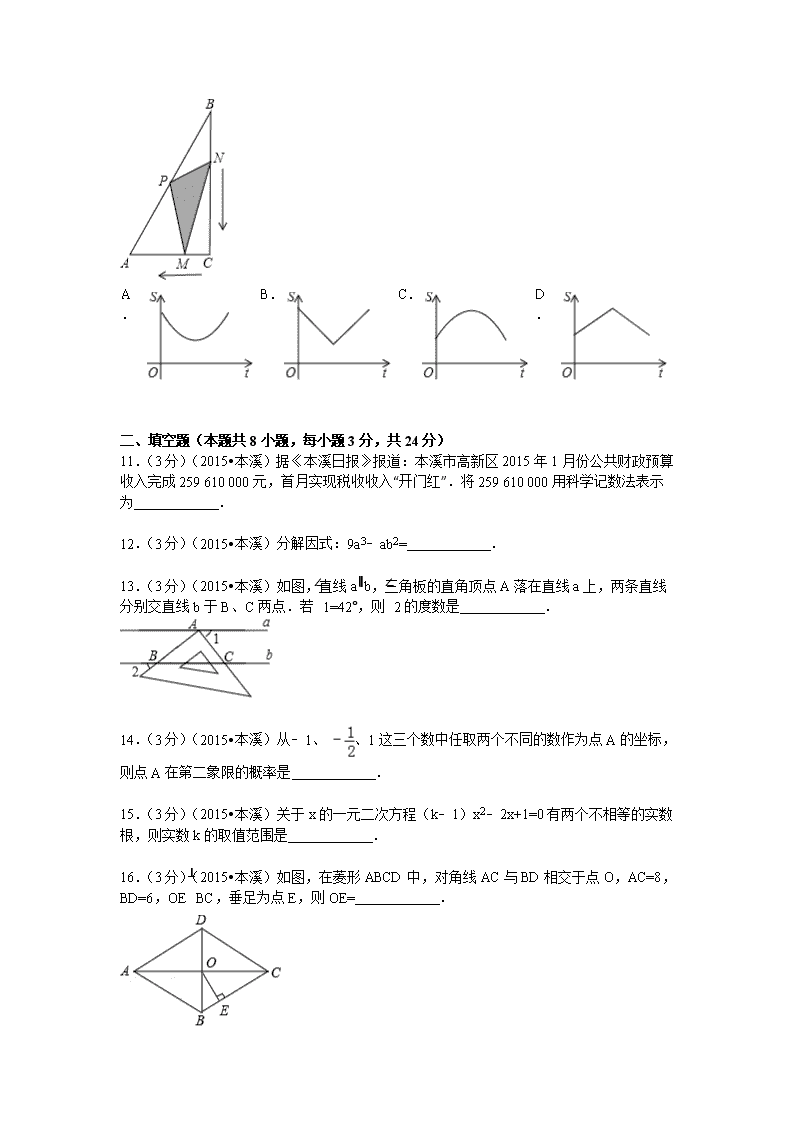
‎2015年辽宁省本溪市中考数学试卷 ‎　‎ 一、选择题（本大题共10小题，每小题3分，共30分．在每小题给出的四个选项中，只有一项是符合题目要求的）‎ ‎1．（3分）（2015•本溪）实数﹣的相反数是（　　）‎ ‎　‎ A．‎ B．‎ ‎﹣‎ C．‎ ‎2‎ D．‎ ‎﹣2‎ ‎　‎ ‎2．（3分）（2015•本溪）如图是由多个完全相同的小正方体组成的几何体，其左视图是（　　）‎ ‎　‎ A．‎ B．‎ C．‎ D．‎ ‎　‎ ‎3．（3分）（2015•本溪）下列运算正确的是（　　）‎ ‎　‎ A．‎ ‎5m+2m=7m2‎ B．‎ ‎﹣2m2•m3=2m5‎ ‎　‎ C．‎ ‎（﹣a2b）3=﹣a6b3‎ D．‎ ‎（b+2a）（2a﹣b）=b2﹣4a2‎ ‎　‎ ‎4．（3分）（2015•本溪）下列图案中既是轴对称图形，又是中心对称图形的是（　　）‎ ‎　‎ A．‎ B．‎ C．‎ D．‎ ‎　‎ ‎5．（3分）（2015•本溪）为迎接“六一”儿童节，某儿童品牌玩具专卖店购进了A、B两类玩具，其中A类玩具的进价比B类玩具的进价每个多3元，经调查：用900元购进A类玩具的数量与用750元购进B类玩具的数量相同．设A类玩具的进价为m元/个，根据题意可列分式方程为（　　）‎ ‎　‎ A．‎ B．‎ C．‎ D．‎ ‎6．（3分）（2015•本溪）射击训练中，甲、乙、丙、丁四人每人射击10次，平均环数均为8.7环，方差分别为S甲2=0.51，S乙2=0.41、S丙2=0.62、S丁2=0.45，则四人中成绩最稳定的是（　　）‎ ‎　‎ A．‎ 甲 B．‎ 乙 C．‎ 丙 D．‎ 丁 ‎　‎ ‎7．（3分）（2015•本溪）在一个不透明的口袋中，装有若干个红球和4个黄球，它们除颜色外没有任何区别，摇匀后从中随机摸出一个球，记下颜色后再放回口袋中，通过大量重复摸球实验发现，摸到黄球的频率是0.2，则估计盒子中大约有红球（　　）‎ ‎　‎ A．‎ ‎16个 B．‎ ‎20个 C．‎ ‎25个 D．‎ ‎30个 ‎　‎ ‎8．（3分）（2015•本溪）如图，▱ABCD的周长为20cm，AE平分∠BAD，若CE=2cm，则AB的长度是（　　）‎ ‎　‎ A．‎ ‎10cm B．‎ ‎8cm C．‎ ‎6cm D．‎ ‎4cm ‎　‎ ‎9．（3分）（2015•本溪）如图，在平面直角坐标系中，直线AB与x轴交于点A（﹣2，0），与x轴夹角为30°，将△ABO沿直线AB翻折，点O的对应点C恰好落在双曲线y=（k≠0）上，则k的值为（　　）‎ ‎　‎ A．‎ ‎4‎ B．‎ ‎﹣2‎ C．‎ D．‎ ‎﹣‎ ‎　‎ ‎10．（3分）（2015•本溪）如图，在△ABC中，∠C=90°，点P是斜边AB的中点，点M从点C向点A匀速运动，点N从点B向点C匀速运动，已知两点同时出发，同时到达终点，连接PM、PN、MN，在整个运动过程中，△PMN的面积S与运动时间t的函数关系图象大致是（　　）‎ ‎　‎ A．‎ B．‎ C．‎ D．‎ ‎　‎ ‎　‎ 二、填空题（本题共8小题，每小题3分，共24分）‎ ‎11．（3分）（2015•本溪）据《本溪日报》报道：本溪市高新区2015年1月份公共财政预算收入完成259 610 000元，首月实现税收收入“开门红”．将259 610 000用科学记数法表示为　　　　　　．‎ ‎　‎ ‎12．（3分）（2015•本溪）分解因式：9a3﹣ab2=　　　　　　．‎ ‎　‎ ‎13．（3分）（2015•本溪）如图，直线a∥b，三角板的直角顶点A落在直线a上，两条直线分别交直线b于B、C两点．若∠1=42°，则∠2的度数是　　　　　　．‎ ‎　‎ ‎14．（3分）（2015•本溪）从﹣1、、1这三个数中任取两个不同的数作为点A的坐标，则点A在第二象限的概率是　　　　　　．‎ ‎　‎ ‎15．（3分）（2015•本溪）关于x的一元二次方程（k﹣1）x2﹣2x+1=0有两个不相等的实数根，则实数k的取值范围是　　　　　　．‎ ‎　‎ ‎16．（3分）（2015•本溪）如图，在菱形ABCD中，对角线AC与BD相交于点O，AC=8，BD=6，OE⊥BC，垂足为点E，则OE=　　　　　　．‎ ‎　‎ ‎17．（3分）（2015•本溪）在△ABC中，AB=6cm，AC=5cm，点D、E分别在AB、AC上．若△ADE与△ABC相似，且S△ADE：S四边形BCED=1：8，则AD=　　　　　　cm．‎ ‎　‎ ‎18．（3分）（2015•本溪）如图，已知矩形ABCD的边长分别为a，b，连接其对边中点，得到四个矩形，顺次连接矩形AEFG各边中点，得到菱形I1；连接矩形FMCH对边中点，又得到四个矩形，顺次连接矩形FNPQ各边中点，得到菱形I2；…如此操作下去，得到菱形In，则In的面积是　　　　　　．‎ ‎　‎ ‎　‎ 三、解答题（第19题10分，第20题12分，共22分）‎ ‎19．（10分）（2015•本溪）先化简，再求值：（x﹣2+）÷，其中x=（π﹣2015）0﹣+（）﹣1．‎ ‎　‎ ‎20．（12分）（2015•本溪）某中学为开拓学生视野，开展“课外读书周”活动，活动后期随机调查了九年级部分学生一周的课外阅读时间，并将结果绘制成两幅不完整的统计图，请你根据统计图的信息回答下列问题：‎ ‎（1）本次调查的学生总数为　　　　　　人，被调查学生的课外阅读时间的中位数是　　　　　　小时，众数是　　　　　　小时；‎ ‎（2）请你补全条形统计图；‎ ‎（3）在扇形统计图中，课外阅读时间为5小时的扇形的圆心角度数是　　　　　　；‎ ‎（4）若全校九年级共有学生700人，估计九年级一周课外阅读时间为6小时的学生有多少人？‎ ‎　‎ ‎　‎ 四、解答题（第21题12分，第22题12分，共24分）‎ ‎21．（12分）（2015•本溪）暑期临近，本溪某旅行社准备组织“亲子一家游”活动，去我省沿海城市旅游，报名的人数共有69人，其中成人的人数比儿童人数的2倍少3人．‎ ‎（1）旅游团中成人和儿童各有多少人？‎ ‎（2）旅行社为了吸引游客，打算给游客准备一件T恤衫，成人T恤衫每购买10件赠送1件儿童T恤衫（不足10件不赠送），儿童T恤衫每件15元，旅行社购买服装的费用不超过1200元，请问每件成人T恤衫的价格最高是多少元？‎ ‎　‎ ‎22．（12分）（2015•本溪）张老师利用休息时间组织学生测量山坡上一棵大树CD的高度，如图，山坡与水平面成30°角（即∠MAN=30°），在山坡底部A处测得大树顶端点C的仰角为45°，沿坡面前进20米，到达B处，又测得树顶端点C的仰角为60°（图中各点均在同一平面内），求这棵大树CD的高度（结果精确到0.1米，参考数据：≈1.732）‎ ‎　‎ ‎　‎ 五、解答题（满分12分）‎ ‎23．（12分）（2015•本溪）如图，点D是等边△ABC中BC边的延长线上一点，且AC=CD，以AB为直径作⊙O，分别交边AC、BC于点E、点F ‎（1）求证：AD是⊙O的切线；‎ ‎（2）连接OC，交⊙O于点G，若AB=4，求线段CE、CG与围成的阴影部分的面积S．‎ ‎　‎ ‎　‎ 六、解答题（满分12分）‎ ‎24．（12分）（2015•本溪）某种商品的进价为40元/件，以获利不低于25%的价格销售时，商品的销售单价y（元/件）与销售数量x（件）（x是正整数）之间的关系如下表：‎ x（件）‎ ‎…‎ ‎5‎ ‎10‎ ‎15‎ ‎20‎ ‎…‎ y（元/件）‎ ‎…‎ ‎75‎ ‎70‎ ‎65‎ ‎60‎ ‎…‎ ‎（1）由题意知商品的最低销售单价是　　　　　　元，当销售单价不低于最低销售单价时，y是x的一次函数．求出y与x的函数关系式及x的取值范围；‎ ‎（2）在（1）的条件下，当销售单价为多少元时，所获销售利润最大，最大利润是多少元？‎ ‎　‎ ‎　‎ 七、解答题（满分12分）‎ ‎25．（12分）（2015•本溪）如图1，在△ABC中，AB=AC，射线BP从BA所在位置开始绕点B顺时针旋转，旋转角为α（0°＜α＜180°）‎ ‎（1）当∠BAC=60°时，将BP旋转到图2位置，点D在射线BP上．若∠CDP=120°，则∠ACD　　　　　　∠ABD（填“＞”、“=”、“＜”），线段BD、CD与AD之间的数量关系是　　　　　　；‎ ‎（2）当∠BAC=120°时，将BP旋转到图3位置，点D在射线BP上，若∠CDP=60°，求证：BD﹣CD=AD；‎ ‎（3）将图3中的BP继续旋转，当30°＜α＜180°时，点D是直线BP上一点（点P不在线段BD上），若∠CDP=120°，请直接写出线段BD、CD与AD之间的数量关系（不必证明）．‎ ‎　‎ ‎　‎ 八、解答题（满分14分）‎ ‎26．（14分）（2015•本溪）如图，抛物线y=ax2+bx（a≠0）经过点A（2，0），点B（3，3），BC⊥x轴于点C，连接OB，等腰直角三角形DEF的斜边EF在x轴上，点E的坐标为（﹣4，0），点F与原点重合 ‎（1）求抛物线的解析式并直接写出它的对称轴；‎ ‎（2）△DEF以每秒1个单位长度的速度沿x轴正方向移动，运动时间为t秒，当点D落在BC边上时停止运动，设△DEF与△OBC的重叠部分的面积为S，求出S关于t的函数关系式；‎ ‎（3）点P是抛物线对称轴上一点，当△ABP时直角三角形时，请直接写出所有符合条件的点P坐标．‎ ‎　‎ ‎　‎ ‎2015年辽宁省本溪市中考数学试卷 参考答案与试题解析 ‎　‎ 一、选择题（本大题共10小题，每小题3分，共30分．在每小题给出的四个选项中，只有一项是符合题目要求的）‎ ‎1．（3分）（2015•本溪）实数﹣的相反数是（　　）‎ ‎　‎ A．‎ B．‎ ‎﹣‎ C．‎ ‎2‎ D．‎ ‎﹣2‎ 考点：‎ 相反数．菁优网版权所有 分析：‎ 根据只有符号不同的两数叫做互为相反数解答．‎ 解答：‎ 解：实数﹣的相反数是，‎ 故选A 点评：‎ 本题考查了实数的性质，熟记相反数的定义是解题的关键．‎ ‎　‎ ‎2．（3分）（2015•本溪）如图是由多个完全相同的小正方体组成的几何体，其左视图是（　　）‎ ‎　‎ A．‎ B．‎ C．‎ D．‎ 考点：‎ 简单组合体的三视图．菁优网版权所有 分析：‎ 根据从左边看得到的图形是左视图，可得答案．‎ 解答：‎ 解：从左边看第一层是三个小正方形，第二层靠左边两个小正方形，第三层靠左边一个小正方形．‎ 故选：C．‎ 点评：‎ 本题考查了简单组合体的三视图，从左边看得到的视图是左视图．‎ ‎　‎ ‎3．（3分）（2015•本溪）下列运算正确的是（　　）‎ ‎　‎ A．‎ ‎5m+2m=7m2‎ B．‎ ‎﹣2m2•m3=2m5‎ ‎　‎ C．‎ ‎（﹣a2b）3=﹣a6b3‎ ‎（b+2a）（2a﹣b）=b2﹣4a2‎ D．‎ 考点：‎ 幂的乘方与积的乘方；合并同类项；单项式乘单项式；平方差公式．菁优网版权所有 分析：‎ A、依据合并同类项法则计算即可；B、依据单项式乘单项式法则计算即可；C、依据积的乘方法则计算即可；D、依据平方差公式计算即可．‎ 解答：‎ 解：A、5m+2m=（5+2）m=7m，故A错误；‎ B、﹣2m2•m3=﹣2m5，故B错误；‎ C、（﹣a2b）3=﹣a6b3，故C正确；‎ D、（b+2a）（2a﹣b）=（2a+b）（2a﹣b）=4a2﹣b2，故D错误．‎ 故选：C．‎ 点评：‎ 本题主要考查的是整式的计算，掌握合并同类项法则、单项式乘单项式法则、积的乘方法则以及平方差公式是解题的关键．‎ ‎　‎ ‎4．（3分）（2015•本溪）下列图案中既是轴对称图形，又是中心对称图形的是（　　）‎ ‎　‎ A．‎ B．‎ C．‎ D．‎ 考点：‎ 中心对称图形；轴对称图形．菁优网版权所有 分析：‎ 根据轴对称图形与中心对称图形的概念求解．‎ 解答：‎ 解：A、不是轴对称图形，也不是中心对称图形；‎ B、既是轴对称图形，又是中心对称图形；‎ C、不是轴对称图形，也不是中心对称图形；‎ D、不是轴对称图形，是中心对称图形．‎ 故选B．‎ 点评：‎ 本题主要考查轴对称图形和中心对称图形的概念，以及对轴对称图形和中心对称图形的认识．‎ ‎　‎ ‎5．（3分）（2015•本溪）为迎接“六一”儿童节，某儿童品牌玩具专卖店购进了A、B两类玩具，其中A类玩具的进价比B类玩具的进价每个多3元，经调查：用900元购进A类玩具的数量与用750元购进B类玩具的数量相同．设A类玩具的进价为m元/个，根据题意可列分式方程为（　　）‎ ‎　‎ A．‎ B．‎ C．‎ D．‎ 考点：‎ 由实际问题抽象出分式方程．菁优网版权所有 分析：‎ 根据题意B类玩具的进价为（m﹣3）元/个，根据用900元购进A类玩具的数量与用750元购进B类玩具的数量相同这个等量关系列出方程即可．‎ 解答：‎ 解：设A类玩具的进价为m元/个，则B类玩具的进价为（m﹣3）元/个，‎ 由题意得，=，‎ 故选：C．‎ 点评：‎ 本题考查的是列分式方程解应用题，找到等量关系是解决问题的关键．‎ ‎　‎ ‎6．（3分）（2015•本溪）射击训练中，甲、乙、丙、丁四人每人射击10次，平均环数均为8.7环，方差分别为S甲2=0.51，S乙2=0.41、S丙2=0.62、S丁2=0.45，则四人中成绩最稳定的是（　　）‎ ‎　‎ A．‎ 甲 B．‎ 乙 C．‎ 丙 D．‎ 丁 考点：‎ 方差．菁优网版权所有 分析：‎ 比较四个人的方差，然后根据方差的意义可判断谁的成绩最稳定．‎ 解答：‎ 解：∵S甲2=0.51，S乙2=0.41、S丙2=0.62、S丁2=0.45，‎ ‎∴S丙2＞S甲2＞S丁2＞S乙2，‎ ‎∴四人中乙的成绩最稳定．‎ 故选B．‎ 点评：‎ 本题考查了方差：方差是反映一组数据的波动大小的一个量．方差越大，则平均值的离散程度越大，稳定性也越小；反之，则它与其平均值的离散程度越小，稳定性越好．‎ ‎　‎ ‎7．（3分）（2015•本溪）在一个不透明的口袋中，装有若干个红球和4个黄球，它们除颜色外没有任何区别，摇匀后从中随机摸出一个球，记下颜色后再放回口袋中，通过大量重复摸球实验发现，摸到黄球的频率是0.2，则估计盒子中大约有红球（　　）‎ ‎　‎ A．‎ ‎16个 B．‎ ‎20个 C．‎ ‎25个 D．‎ ‎30个 考点：‎ 利用频率估计概率．菁优网版权所有 分析：‎ 利用大量重复实验时，事件发生的频率在某个固定位置左右摆动，并且摆动的幅度越来越小，根据这个频率稳定性定理，可以用频率的集中趋势来估计概率，这个固定的近似值就是这个事件的概率．‎ 解答：‎ 解：设红球有x个，根据题意得，‎ ‎4：（4+x）=1：5，‎ 解得x=16．‎ 故选A．‎ 点评：‎ 此题主要考查了利用频率估计概率，正确运用概率公式是解题关键．‎ ‎　‎ ‎8．（3分）（2015•本溪）如图，▱ABCD的周长为20cm，AE平分∠BAD，若CE=2cm，则AB的长度是（　　）‎ ‎　‎ A．‎ ‎10cm B．‎ ‎8cm C．‎ ‎6cm D．‎ ‎4cm 考点：‎ 平行四边形的性质．菁优网版权所有 分析：‎ 根据平行四边形的性质得出AB=CD，AD=BC，AD∥BC，推出∠DAE=∠BAE，求出∠BAE=∠AEB，推出AB=BE，设AB=CD=xcm，则AD=BC=（x+2）cm，得出方程x+x+2=10，求出方程的解即可．‎ 解答：‎ 解：∵四边形ABCD是平行四边形，‎ ‎∴AB=CD，AD=BC，AD∥BC，‎ ‎∴∠DAE=∠BAE，‎ ‎∵AE平分∠BAD，‎ ‎∴∠DAE=∠BAE，‎ ‎∴∠BAE=∠AEB，‎ ‎∴AB=BE，‎ 设AB=CD=xcm，则AD=BC=（x+2）cm，‎ ‎∵▱ABCD的周长为20cm，‎ ‎∴x+x+2=10，‎ 解得：x=4，‎ 即AB=4cm，‎ 故选D．‎ 点评：‎ 本题考查了平行四边形的在，平行线的性质，等腰三角形的判定的应用，解此题的关键是能推出AB=BE，题目比较好，难度适中．‎ ‎　‎ ‎9．（3分）（2015•本溪）如图，在平面直角坐标系中，直线AB与x轴交于点A（﹣2，0），与x轴夹角为30°，将△ABO沿直线AB翻折，点O的对应点C恰好落在双曲线y=（k≠0）上，则k的值为（　　）‎ ‎　‎ A．‎ ‎4‎ B．‎ ‎﹣2‎ C．‎ D．‎ ‎﹣‎ 考点：‎ 翻折变换（折叠问题）；待定系数法求反比例函数解析式．菁优网版权所有 分析：‎ 设点C的坐标为（x，y），过点C作CD⊥x轴，作CE⊥y轴，由折叠的性质易得∠CAB=∠OAB=30°，AC=AO=2，∠ACB=AOB=90°，用锐角三角函数的定义得CD，CE，得点C的坐标，易得k．‎ 解答：‎ 解：设点C的坐标为（x，y），过点C作CD⊥x轴，作CE⊥y轴，‎ ‎∵将△ABO沿直线AB翻折，‎ ‎∴∠CAB=∠OAB=30°，AC=AO=2，∠ACB=AOB=90°，‎ ‎∴CD=y=AC•sin60°=2×=，‎ ‎∵∠ACB=∠DCE=90°，‎ ‎∴∠BCE=∠ACD=30°，‎ ‎∵BC=BO=AO•tan30°=2×=，‎ CE=x=BC•cos30°==1，‎ ‎∵点C恰好落在双曲线y=（k≠0）上，‎ ‎∴k=x•y=﹣1×=﹣，‎ 故选D．‎ 点评：‎ 本题主要考查了翻折的性质，锐角三角函数，反比例函数的解析式，理解翻折的性质，求点C的坐标是解答此题的关键．‎ ‎　‎ ‎10．（3分）（2015•本溪）如图，在△ABC中，∠C=90°，点P是斜边AB的中点，点M从点C向点A匀速运动，点N从点B向点C匀速运动，已知两点同时出发，同时到达终点，连接PM、PN、MN，在整个运动过程中，△PMN的面积S与运动时间t的函数关系图象大致是（　　）‎ ‎　‎ A．‎ B．‎ C．‎ D．‎ 考点：‎ 动点问题的函数图象．菁优网版权所有 分析：‎ 首先连接CP，根据点P是斜边AB的中点，可得S△ACP=S△BCP=S△ABC ‎；然后分别求出出发时；点N到达BC的中点、点M也到达AC的中点时；结束时，△PMN的面积S的大小，即可推得△MPQ的面积大小变化情况是：先减小后增大，而且是以抛物线的方式变化，据此判断出△PMN的面积S与运动时间t的函数关系图象大致是哪个即可．‎ 解答：‎ 解：如图1，连接CP，‎ ‎，‎ ‎∵点P是斜边AB的中点，‎ ‎∴S△ACP=S△BCP=S△ABC，‎ 出发时，S△PMN=S△BCP=S△ABC；‎ ‎∵两点同时出发，同时到达终点，‎ ‎∴点N到达BC的中点时，点M也到达AC的中点，‎ ‎∴S△PMN=S△ABC；‎ 结束时，S△PMN=S△ACP=S△ABC，‎ ‎△MPQ的面积大小变化情况是：先减小后增大，而且是以抛物线的方式变化，‎ ‎∴△PMN的面积S与运动时间t的函数关系图象大致是：‎ ‎．‎ 故选：A．‎ 点评：‎ 此题主要考查了动点问题的函数图象，要熟练掌握，解答此题的关键是要明确：函数图象是典型的数形结合，图象应用信息广泛，通过看图获取信息，不仅可以解决生活中的实际问题，还可以提高分析问题、解决问题的能力．用图象解决问题时，要理清图象的含义即会识图．‎ ‎　‎ 二、填空题（本题共8小题，每小题3分，共24分）‎ ‎11．（3分）（2015•本溪）据《本溪日报》报道：本溪市高新区2015年1月份公共财政预算收入完成259 610 000元，首月实现税收收入“开门红”．将259 610 000用科学记数法表示为　2.5961×108　．‎ 考点：‎ 科学记数法—表示较大的数．菁优网版权所有 分析：‎ 科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数．确定n的值时，要看把原数变成a时，小数点移动了多少位，n的绝对值与小数点移动的位数相同．当原数绝对值＞1时，n是正数；当原数的绝对值＜1时，n是负数．‎ 解答：‎ 解：将259 610 000用科学记数法表示为2.5961×108．‎ 故答案为：2.5961×108．‎ 点评：‎ 此题考查科学记数法的表示方法．科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数，表示时关键要正确确定a的值以及n的值．‎ ‎　‎ ‎12．（3分）（2015•本溪）分解因式：9a3﹣ab2=　a（3a﹣b）（3a+b）　．‎ 考点：‎ 提公因式法与公式法的综合运用．菁优网版权所有 分析：‎ 观察原式9a3﹣ab2，找到公因式a，提取公因式a后发现9a2﹣b2是平方差公式，再利用平方差公式继续分解．‎ 解答：‎ 解：9a3﹣ab2，‎ ‎=a（9a2﹣b2），‎ ‎=a（3a﹣b）（3a+b）．‎ 点评：‎ 本题考查了用提公因式法和公式法进行因式分解，一个多项式有公因式首先提取公因式，然后再用其他方法进行因式分解，同时因式分解要彻底，直到不能分解为止．‎ ‎　‎ ‎13．（3分）（2015•本溪）如图，直线a∥b，三角板的直角顶点A落在直线a上，两条直线分别交直线b于B、C两点．若∠1=42°，则∠2的度数是　48°　．‎ 考点：‎ 平行线的性质．菁优网版权所有 分析：‎ 先根据两角互余的性质求出∠3的度数，再由平行线的性质即可得出结论．‎ 解答：‎ 解：∵∠BAC=90°，∠1=42°，‎ ‎∴∠3=90°﹣∠1=90°﹣42°=48°．‎ ‎∵直线a∥b，‎ ‎∴∠2=∠3=48°．‎ 故答案为：48°．‎ 点评：‎ 本题考查的是平行线的性质，用到的知识点为：两直线平行，同位角相等．‎ ‎　‎ ‎14．（3分）（2015•本溪）从﹣1、、1这三个数中任取两个不同的数作为点A的坐标，则点A在第二象限的概率是　　．‎ 考点：‎ 列表法与树状图法；点的坐标．菁优网版权所有 专题：‎ 计算题．‎ 分析：‎ 先画树状图展示所有6种等可能的结果数，而点（﹣1，1）和（﹣，1）在第二象限，然后根据概率公式求解．‎ 解答：‎ 解：画树状图为：‎ 共有6种等可能的结果数，其中在第二象限的点有2个，‎ 所以点A在第二象限的概率==．‎ 故答案为．‎ 点评：‎ 本题考查了列表法或树状图法：通过列表法或树状图法展示所有等可能的结果求出n，再从中选出符合事件A或B的结果数目m，然后根据概率公式求出事件A或B的概率．‎ ‎　‎ ‎15．（3分）（2015•本溪）关于x的一元二次方程（k﹣1）x2﹣2x+1=0有两个不相等的实数根，则实数k的取值范围是　k＜2且k≠1　．‎ 考点：‎ 根的判别式；一元二次方程的定义．菁优网版权所有 分析：‎ 根据一元二次方程的定义和判别式的意义得到k﹣1≠0且△=（﹣2）2﹣4（k﹣1）＞0，然后求出两个不等式的公共部分即可．‎ 解答：‎ 解：∵关于x的一元二次方程（k﹣1）x2﹣2x+1=0有两个不相等的实数根，‎ ‎∴k﹣1≠0且△=（﹣2）2﹣4（k﹣1）＞0，‎ 解得：k＜2且k≠1．‎ 故答案为：k＜2且k≠1．‎ 点评：‎ 本题考查了一元二次方程ax2+bx+c=0（a≠0）的根的判别式△=b2﹣4ac：当△＞0，方程有两个不相等的实数根；当△=0，方程有两个相等的实数根；当△＜0，方程没有实数根．‎ ‎　‎ ‎16．（3分）（2015•本溪）如图，在菱形ABCD中，对角线AC与BD相交于点O，AC=8，BD=6，OE⊥BC，垂足为点E，则OE=　　．‎ 考点：‎ 菱形的性质．菁优网版权所有 专题：‎ 计算题．‎ 分析：‎ 先根据菱形的性质得AC⊥BD，OB=OD=BD=3，OA=OC=AC=4，再在Rt△OBC中利用勾股定理计算出BC=5，然后利用面积法计算OE的长．‎ 解答：‎ 解：∵四边形ABCD为菱形，‎ ‎∴AC⊥BD，OB=OD=BD=3，OA=OC=AC=4，‎ 在Rt△OBC中，∵OB=3，OC=4，‎ ‎∴BC==5，‎ ‎∵OE⊥BC，‎ ‎∴OE•BC=OB•OC，‎ ‎∴OE==．‎ 故答案为．‎ 点评：‎ 本题考查了菱形的性质：菱形具有平行四边形的一切性质；菱形的四条边都相等；菱形的两条对角线互相垂直，并且每一条对角线平分一组对角．也考查了勾股定理和三角形面积公式．‎ ‎　‎ ‎17．（3分）（2015•本溪）在△ABC中，AB=6cm，AC=5cm，点D、E分别在AB、AC上．若△ADE与△ABC相似，且S△ADE：S四边形BCED=1：8，则AD=　2或　cm．‎ 考点：‎ 相似三角形的性质．菁优网版权所有 专题：‎ 分类讨论．‎ 分析：‎ 由于△ADE与△ABC相似，但其对应角不能确定，所以应分两种情况进行讨论．‎ 解答：‎ 解：∵S△ADE：S四边形BCED=1：8，‎ ‎∴S△ADE：S△ABC=1：9，‎ ‎∴△ADE与△ABC相似比为：1：3，‎ ‎①若∠AED对应∠B时，‎ 则，‎ ‎∵AC=5cm，‎ ‎∴AD=cm；‎ ‎②当∠ADE对应∠B时，则，‎ ‎∵AB=6cm，‎ ‎∴AD=2cm；‎ 故答案为：．‎ 点评：‎ 本题考查的是相似三角形的性质，相似三角形的对应边成比例，相似三角形的面积比等于相似比的平方，意识到有两种情况分类讨论是解决问题的关键．‎ ‎　‎ ‎18．（3分）（2015•本溪）如图，已知矩形ABCD的边长分别为a，b，连接其对边中点，得到四个矩形，顺次连接矩形AEFG各边中点，得到菱形I1；连接矩形FMCH对边中点，又得到四个矩形，顺次连接矩形FNPQ各边中点，得到菱形I2；…如此操作下去，得到菱形In，则In的面积是　（）2n+1ab　．‎ 考点：‎ 中点四边形．菁优网版权所有 专题：‎ 规律型．‎ 分析：‎ 利用菱形的面积为两对角线乘积的一半，得到菱形I1 的面积，同理可得菱形I2的面积，根据规律可得菱形In的面积．‎ 解答：‎ 解：由题意得：菱形I1 的面积为：×AG×AE=×=（）3•ab；‎ 菱形I2的面积为：×FQ×FN=×（×）×（b）=（）5•ab；‎ ‎…，‎ ‎∴菱形In的面积为：（）2n+1ab，‎ 故答案为：（）2n+1ab．‎ 点评：‎ 本题主要考查了菱形面积的计算和规律的归纳，利用菱形的面积为两对角线乘积的一半，是解答此题的关键．‎ ‎　‎ 三、解答题（第19题10分，第20题12分，共22分）‎ ‎19．（10分）（2015•本溪）先化简，再求值：（x﹣2+）÷，其中x=（π﹣2015）0﹣+（）﹣1．‎ 考点：‎ 分式的化简求值；零指数幂；负整数指数幂．菁优网版权所有 分析：‎ 先通分，然后进行四则运算，最后将x的值求出来，再代入计算即可．‎ 解答：‎ 解：原式=‎ ‎=‎ ‎=‎ ‎=‎ ‎=1﹣2+3=2，‎ 当x=2时，原式=．‎ 点评：‎ 本题考查了分式的化简求值，解答此题的关键是把分式化到最简，然后代值计算．‎ ‎　‎ ‎20．（12分）（2015•本溪）某中学为开拓学生视野，开展“课外读书周”活动，活动后期随机调查了九年级部分学生一周的课外阅读时间，并将结果绘制成两幅不完整的统计图，请你根据统计图的信息回答下列问题：‎ ‎（1）本次调查的学生总数为　50　人，被调查学生的课外阅读时间的中位数是　4　小时，众数是　5　小时；‎ ‎（2）请你补全条形统计图；‎ ‎（3）在扇形统计图中，课外阅读时间为5小时的扇形的圆心角度数是　144°　；‎ ‎（4）若全校九年级共有学生700人，估计九年级一周课外阅读时间为6小时的学生有多少人？‎ 考点：‎ 条形统计图；用样本估计总体；扇形统计图；中位数；众数．菁优网版权所有 分析：‎ ‎（1）根据统计图可知，课外阅读达3小时的共10人，占总人数的20%，由此可得出总人数；求出课外阅读时间4小时与6小时男生的人数，再根据中位数与众数的定义即可得出结论；‎ ‎（2）根据（1）中求出的人数补全条形统计图即可；‎ ‎（3）求出课外阅读时间为5小时的人数，再求出其人数与总人数的比值即可得出扇形的圆心角度数；‎ ‎（4）求出总人数与课外阅读时间为6小时的学生人数的百分比的积即可．‎ 解答：‎ 解：（1）∵课外阅读达3小时的共10人，占总人数的20%，‎ ‎∴=50（人）．‎ ‎∵课外阅读4小时的人数是32%，‎ ‎∴50×32%=16（人），‎ ‎∴男生人数=16﹣8=8（人）；‎ ‎∴课外阅读6小时的人数=50﹣6﹣4﹣8﹣8﹣8﹣12﹣3=1（人），‎ ‎∴课外阅读3小时的是10人，4小时的是16人，5小时的是20人，6小时的是4人，‎ ‎∴中位数是4小时，众数是5小时．‎ 故答案为：50，4，5‎ ‎（2）如图所示．‎ ‎（3）∵课外阅读5小时的人数是20人，‎ ‎∴×360°=144°．‎ 故答案为：144°；‎ ‎（4）∵课外阅读5小时的人数是4人，‎ ‎∴700×=56（人）．‎ 答：九年级一周课外阅读时间为6小时的学生大约有56人．‎ 点评：‎ 本题考查的是条形统计图，熟知条形统计图与扇形统计图的特点是解答此题的关键．‎ ‎　‎ 四、解答题（第21题12分，第22题12分，共24分）‎ ‎21．（12分）（2015•本溪）暑期临近，本溪某旅行社准备组织“亲子一家游”活动，去我省沿海城市旅游，报名的人数共有69人，其中成人的人数比儿童人数的2倍少3人．‎ ‎（1）旅游团中成人和儿童各有多少人？‎ ‎（2）旅行社为了吸引游客，打算给游客准备一件T恤衫，成人T恤衫每购买10件赠送1件儿童T恤衫（不足10件不赠送），儿童T恤衫每件15元，旅行社购买服装的费用不超过1200元，请问每件成人T恤衫的价格最高是多少元？‎ 考点：‎ 一元一次不等式的应用；一元一次方程的应用．菁优网版权所有 分析：‎ ‎（1）设旅游团中儿童有x人，则成人有（2x﹣3）人，根据报名的人数共有69人，列方程求解；‎ ‎（2）根据题意可得能赠送4件儿童T恤衫，设每件成人T恤衫的价格是m元，根据旅行社购买服装的费用不超过1200元，列不等式求解．‎ 解答：‎ 解：（1）设旅游团中儿童有x人，则成人有（2x﹣3）人，‎ 根据题意得x+（2x﹣3）=69，‎ 解得：x=24，‎ 则2x﹣3=2×24﹣3=45．‎ 答：旅游团中成人有45人，儿童有24人；‎ ‎（2）∵45÷10=4.5，‎ ‎∴可赠送4件儿童T恤衫，‎ 设每件成人T恤衫的价格是m元，‎ 根据题意可得45x+15（24﹣4）≤1200，‎ 解得：x≤20．‎ 答：每件成人T恤衫的价格最高是20元．‎ 点评：‎ 本题考查了一元一次不等式和一元一次方程的应用，解答本题的关键是读懂题意，设出未知数，找出合适的等量关系，列方程和不等式求解．‎ ‎　‎ ‎22．（12分）（2015•本溪）张老师利用休息时间组织学生测量山坡上一棵大树CD的高度，如图，山坡与水平面成30°角（即∠MAN=30°），在山坡底部A处测得大树顶端点C的仰角为45°，沿坡面前进20米，到达B处，又测得树顶端点C的仰角为60°（图中各点均在同一平面内），求这棵大树CD的高度（结果精确到0.1米，参考数据：≈1.732）‎ 考点：‎ 解直角三角形的应用-仰角俯角问题．菁优网版权所有 分析：‎ 过B作BE⊥CD交CD延长线于E，由∠CAN=45°，∠MAN=30°，得到∠CAB=15°，由∠CBD=60°，∠DBE=30°，得到∠CBD=30°于是有∠CAB=∠ACB=15°所以AB=BC=20，解Rt△BCE，可求得CE，解Rt△DBE可求得DE，CE﹣DE即得到树高CD．‎ 解答：‎ 解：如图，过B作BE⊥CD交CD延长线于E，‎ ‎∵∠CAN=45°，∠MAN=30°，‎ ‎∴∠CAB=15°‎ ‎∵∠CBD=60°，∠DBE=30°，‎ ‎∴∠CBD=30°，‎ ‎∵∠CBE=∠CAB+∠ACB，‎ ‎∴∠CAB=∠ACB=15°，‎ ‎∴AB=BC=20，‎ 在Rt△BCE中，∠CBE=60°，BC=20，‎ ‎∴CE=BCsin∠CBE=20×BE=BCcos∠CBE=20×0.5=10，‎ 在Rt△DBE中，∠DBE=30°，BE=10，‎ ‎∴DE=BEtan∠DBE=10×，‎ ‎∴CD=CE﹣DE=≈11.5，‎ 答：这棵大树CD的高度大约为11.5米．‎ 点评：‎ 本题主要考查了等腰三角形的判定与性质，解直角三角形，要求学生能借助俯角、仰角构造直角三角形，并结合图形利用三角函数解直角三角形．‎ ‎　‎ 五、解答题（满分12分）‎ ‎23．（12分）（2015•本溪）如图，点D是等边△ABC中BC边的延长线上一点，且AC=CD，以AB为直径作⊙O，分别交边AC、BC于点E、点F ‎（1）求证：AD是⊙O的切线；‎ ‎（2）连接OC，交⊙O于点G，若AB=4，求线段CE、CG与围成的阴影部分的面积S．‎ 考点：‎ 切线的判定；等边三角形的判定与性质；扇形面积的计算．菁优网版权所有 分析：‎ ‎（1）求出∠DAC=30°，即可求出∠DAB=90°，根据切线的判定推出即可；‎ ‎（2）连接OE，分别求出△AOE、△AOC，扇形OEG的面积，即可求出答案．‎ 解答：‎ ‎（1）证明：∵△ABC为等边三角形，‎ ‎∴AC=BC，‎ 又∵AC=CD，‎ ‎∴AC=BC=CD，‎ ‎∴△ABD为直角三角形，‎ ‎∴AB⊥AD，‎ ‎∵AB为直径，‎ ‎∴AD是⊙O的切线；‎ ‎（2）解：连接OE，‎ ‎∵OA=OE，∠BAC=60°，‎ ‎∴△OAE是等边三角形，‎ ‎∴∠AOE=60°，‎ ‎∵CB=BA，OA=OB，‎ ‎∴CO⊥AB，‎ ‎∴∠AOC=90°，‎ ‎∴∠EOC=30°，‎ ‎∵△ABC是边长为4的等边三角形，‎ ‎∴AO=2，由勾股定理得：OC==2，‎ 同理等边三角形AOE边AO上高是=，‎ S阴影=S△AOC﹣S等边△AOE﹣S扇形EOG==．‎ 点评：‎ 本题考查了等边三角形的性质和判定，勾股定理，三角形面积，扇形的面积，切线的判定的应用，能综合运用定理进行推理和计算是解此题的关键．‎ ‎　‎ 六、解答题（满分12分）‎ ‎24．（12分）（2015•本溪）某种商品的进价为40元/件，以获利不低于25%的价格销售时，商品的销售单价y（元/件）与销售数量x（件）（x是正整数）之间的关系如下表：‎ x（件）‎ ‎…‎ ‎5‎ ‎10‎ ‎15‎ ‎20‎ ‎…‎ y（元/件）‎ ‎…‎ ‎75‎ ‎70‎ ‎65‎ ‎60‎ ‎…‎ ‎（1）由题意知商品的最低销售单价是　50　元，当销售单价不低于最低销售单价时，y是x的一次函数．求出y与x的函数关系式及x的取值范围；‎ ‎（2）在（1）的条件下，当销售单价为多少元时，所获销售利润最大，最大利润是多少元？‎ 考点：‎ 二次函数的应用．菁优网版权所有 分析：‎ ‎（1）由40（1+25%）即可得出最低销售单价；根据题意由待定系数法求出y与x的函数关系式和x的取值范围；‎ ‎（2）设所获利润为P元，由题意得出P是x的二次函数，即可得出结果．‎ 解答：‎ 解：（1）40（1+25%）=50（元），‎ 故答案为：50；‎ 设y=kx+b，‎ 根据题意得：，‎ 解得：k=﹣1，b=80，‎ ‎∴y=﹣x+80，‎ 根据题意得：，且x为正整数，‎ ‎∴0＜x≤30，x为正整数，‎ ‎∴y=﹣x+80（0≤x≤30，且x为正整数）‎ ‎（2）设所获利润为P元，根据题意得：‎ P=（y﹣40）•x=（﹣x+80﹣40）x=﹣（x﹣20）2+400，‎ 即P是x的二次函数，‎ ‎∵a=﹣1＜0，‎ ‎∴P有最大值，‎ ‎∴当x=20时，P最大值=400，此时y=60，‎ ‎∴当销售单价为60元时，所获利润最大，最大利润为400元．‎ 点评：‎ 本题考查了二次函数的应用、用待定系数法求一次函数的解析式、二次函数的最值问题；由题意求出一次函数和二次函数的解析式是解决问题的关键．‎ ‎　‎ 七、解答题（满分12分）‎ ‎25．（12分）（2015•本溪）如图1，在△ABC中，AB=AC，射线BP从BA所在位置开始绕点B顺时针旋转，旋转角为α（0°＜α＜180°）‎ ‎（1）当∠BAC=60°时，将BP旋转到图2位置，点D在射线BP上．若∠CDP=120°，则∠ACD　=　∠ABD（填“＞”、“=”、“＜”），线段BD、CD与AD之间的数量关系是　BD=CD+AD　；‎ ‎（2）当∠BAC=120°时，将BP旋转到图3位置，点D在射线BP上，若∠CDP=60°，求证：BD﹣CD=AD；‎ ‎（3）将图3中的BP继续旋转，当30°＜α＜180°时，点D是直线BP上一点（点P不在线段BD上），若∠CDP=120°，请直接写出线段BD、CD与AD之间的数量关系（不必证明）．‎ 考点：‎ 几何变换综合题．菁优网版权所有 分析：‎ ‎（1）如图2，由∠CDP=120°，根据邻补角互补得出∠CDB=60°，那么∠CDB=∠BAC=60°，所以A、B、C、D四点共圆，根据圆周角定理得出∠ACD=∠ABD；在BP上截取BE=CD，连接AE．利用SAS证明△DCA≌△EBA，得出AD=AE，∠DAC=∠EAB，再证明△ADE是等边三角形，得到DE=AD，进而得出BD=CD+AD．‎ ‎（2）如图3，设AC与BD相交于点O，在BP上截取BE=CD，连接AE，过A作AF⊥BD于F．先由两角对应相等的两三角形相似得出△DOC∽△AOB，于是∠DCA=∠EBA．再利用SAS证明△DCA≌△EBA，得出AD=AE，∠DAC=∠EAB．由∠CAB=∠CAE+∠EAB=120°，得出∠DAE=120°，根据等腰三角形的性质及三角形内角和定理求出∠ADE=∠AED==30°．解Rt△ADF，得到DF=AD，那么DE=2DF=AD，进而得出BD=DE+BE=AD+CD，即BD﹣CD=AD；‎ ‎（3）同（2）证明可以得出BD+CD=AD．‎ 解答：‎ 解：（1）如图2，∵∠CDP=120°，‎ ‎∴∠CDB=60°，‎ ‎∵∠BAC=60°，‎ ‎∴∠CDB=∠BAC=60°，‎ ‎∴A、B、C、D四点共圆，‎ ‎∴∠ACD=∠ABD．‎ 在BP上截取BE=CD，连接AE．‎ 在△DCA与△EBA中，‎ ‎，‎ ‎∴△DCA≌△EBA（SAS），‎ ‎∴AD=AE，∠DAC=∠EAB，‎ ‎∵∠CAB=∠CAE+∠EAB=60°，‎ ‎∴∠DAE=60°，‎ ‎∴△ADE是等边三角形，‎ ‎∴DE=AD．‎ ‎∵BD=BE+DE，‎ ‎∴BD=CD+AD．‎ 故答案为=，BD=CD+AD；‎ ‎（2）如图3，设AC与BD相交于点O，在BP上截取BE=CD，连接AE，过A作AF⊥BD于F．‎ ‎∵∠CDP=60°，‎ ‎∴∠CDB=120°．‎ ‎∵∠CAB=120°，‎ ‎∴∠CDB=∠CAB，‎ ‎∵∠DOC=∠AOB，‎ ‎∴△DOC∽△AOB，‎ ‎∴∠DCA=∠EBA．‎ 在△DCA与△EBA中，‎ ‎，‎ ‎∴△DCA≌△EBA（SAS），‎ ‎∴AD=AE，∠DAC=∠EAB．‎ ‎∵∠CAB=∠CAE+∠EAB=120°，‎ ‎∴∠DAE=120°，‎ ‎∴∠ADE=∠AED==30°．‎ ‎∵在Rt△ADF中，∠ADF=30°，‎ ‎∴DF=AD，‎ ‎∴DE=2DF=AD，‎ ‎∴BD=DE+BE=AD+CD，‎ ‎∴BD﹣CD=AD；‎ ‎（3）BD+CD=AD．‎ 点评：‎ 本题是几何变换综合题，其中涉及到四点共圆，圆周角定理，全等三角形、相似三角形的判定与性质，等边三角形的判定与性质，等腰三角形的性质，三角形内角和定理等知识，综合性较强，难度适中．准确作出辅助线证明△DCA≌△EBA是解题的关键．‎ ‎　‎ 八、解答题（满分14分）‎ ‎26．（14分）（2015•本溪）如图，抛物线y=ax2+bx（a≠0）经过点A（2，0），点B（3，3），BC⊥x轴于点C，连接OB，等腰直角三角形DEF的斜边EF在x轴上，点E的坐标为（﹣4，0），点F与原点重合 ‎（1）求抛物线的解析式并直接写出它的对称轴；‎ ‎（2）△DEF以每秒1个单位长度的速度沿x轴正方向移动，运动时间为t秒，当点D落在BC边上时停止运动，设△DEF与△OBC的重叠部分的面积为S，求出S关于t的函数关系式；‎ ‎（3）点P是抛物线对称轴上一点，当△ABP时直角三角形时，请直接写出所有符合条件的点P坐标．‎ 考点：‎ 二次函数综合题．菁优网版权所有 分析：‎ ‎（1）根据待定系数法解出解析式和对称轴即可；‎ ‎（2）从三种情况分析①当0≤t≤3时，△DEF与△OBC重叠部分为等腰直角三角形；②当3＜t≤4时，△DEF与△OBC重叠部分是四边形；③当4＜t≤5时，△DEF与△OBC重叠部分是四边形得出S关于t的函数关系式即可；‎ ‎（3）直接写出当△ABP时直角三角形时符合条件的点P坐标．‎ 解答：‎ 解：（1）根据题意得，‎ 解得a=1，b=﹣2，‎ ‎∴抛物线解析式是y=x2﹣2x，‎ 对称轴是直线x=1；‎ ‎（2）有3中情况：‎ ‎①当0≤t≤3时，△DEF与△OBC重叠部分为等腰直角三角形，如图1：‎ S=；‎ ‎②当3＜t≤4时，△DEF与△OBC重叠部分是四边形，如图2：‎ S=；‎ ‎③当4＜t≤5时，△DEF与△OBC重叠部分是四边形，如图3：‎ S=；‎ ‎（3）当△ABP时直角三角形时，可得符合条件的点P坐标为（1，1）或（1，2）或（1，）或（1，）．‎ 点评：‎ 此题考查了难度较大的函数与几何的综合题，关键是根据0≤t≤3，3＜t≤4，4＜t≤5三种情况进行分析．‎ ‎　‎