- 2021-05-10 发布 |
- 37.5 KB |
- 5页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
中考备考复习反比例函数的一些常考相关结论图片版
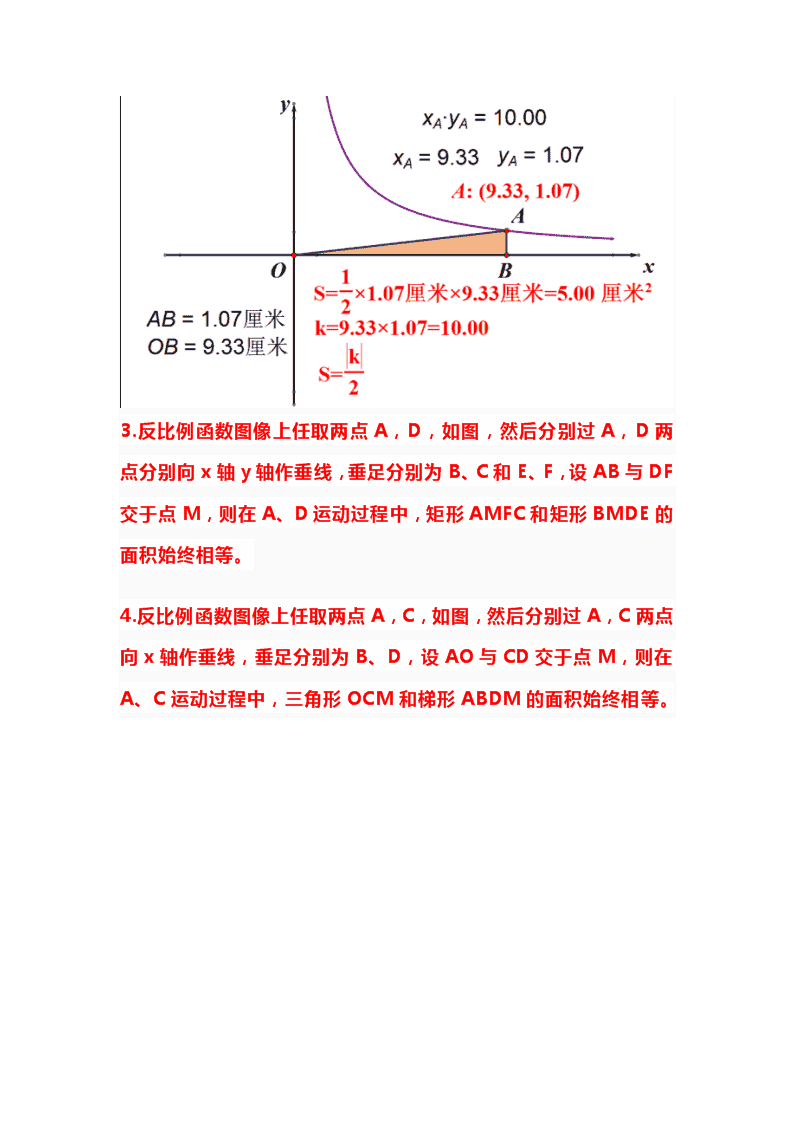
反比例函数的一些常考相关结论 反比例函数是中考的重要内容之一,关于反比例函数的一些相关结论大概可以分为以下四类: 1.反比例中的面积关系; 2.反比例中的平行关系; 3.反比例中的线段关系; 4.反比例中的角的关系。 一.有关面积关系: 1.反比例函数图像上任取一点A,然后过A点分别向x轴,y轴作垂线,垂足分别为为B、C,则矩形ABOC的面积始终等于k的绝对值。 2.反比例函数图像上任取一点A,然后过A点向x轴作垂线,垂足为为B,则三角形ABO的面积始终等于k的绝对值的一半。 3.反比例函数图像上任取两点A,D,如图,然后分别过A,D两点分别向x轴y轴作垂线,垂足分别为B、C和E、F,设AB与DF交于点M,则在A、D运动过程中,矩形AMFC和矩形BMDE的面积始终相等。 4.反比例函数图像上任取两点A,C,如图,然后分别过A,C两点向x轴作垂线,垂足分别为B、D,设AO与CD交于点M,则在A、C运动过程中,三角形OCM和梯形ABDM的面积始终相等。 4.反比例函数图像上任取两点A,C,如图,然后分别过A,C两点向x轴作垂线,垂足分别为B、D,则在A、C运动过程中,三角形OCA和梯形ABDC的面积始终相等。 5.矩形ABOC的边OC、OB分别在x轴y轴上,如图,AB边与反比例函数图像交于点D,AC边与反比例函数图像交于点E,连接OA、OD、OE,则三角形OAD和三角形OAE的面积相等。 二.有关平行关系: 1.矩形ABCO的边OC、OA分别在x轴y轴上,如图,AB边与反比例函数图像交于点D,BC边与反比例函数图像交于点E,连接AC、DE,则DE∥AC。 2.反比例函数图象上任取两点A、B向坐标轴作垂线,然后连接垂足C、D或者E、F,则AB∥CD,AB∥EF. 三.有关线段关系: 1.反比例函数图象与正比例函数的图象交于A、B两点,则OA=OB. 2.反比例函数图象若与一次函数的图象交于A、B两点,与坐标轴交于点C、D,则AD=BC,AC=BD. 3.反比例函数图象与正比例函数的图象交于A、B两点,过点A作y轴垂线,垂足为C,连接BC并延长交反比例函数的图象于点D,连接AD,则DA=DC. 3.反比例函数图象上任取一点A,过点A作y轴垂线,垂足为C,作AC的垂直平分线与反比例函数的图象于点B,与x轴交于点D,连接AD、DC、CB、BA,则AD=DC=CB=BA(即四边形ABCD是菱形). 4.矩形ABCO的边OC、OA分别在x轴y轴上,如图,AB边与反比例函数图像交于点D,BC边与反比例函数图像交于点E,则AD:DB=CE:EB. 5.反比例函数图像上任取两点A、D两点,分别过A点和D点作x轴和y轴的垂线,垂足分别为B和F,AB和FD交于点M,则FM:MD=BM:MA. 四.有关角的关系: 1.点A和点B是反比例函数图像两点,C点是x轴上一点,D点是y轴上一点,四边形ABCD是平行四边形,如图,则∠1=∠2,∠3=∠4. 2.点A和点B是反比例函数图像两点,C点是x轴上一点,D点是y轴上一点,四边形ABCD是平行四边形,延长AD交x轴于点E,延长BC交y轴于点F,连接EF,如图,则∠1=∠2,∠3=∠4,∠5=∠6,∠7=∠8,四边形DCFE为菱形。 3.点A和点B是反比例函数图像两点,直线AB与x轴交于点F,与y轴交于点E,连接AO并延长交反比例函数图象的另一支曲线于点C,连接BC交y轴于点D,交x轴于G,则∠1=∠2,∠3=∠4,BD=BE,BF=BG。查看更多