中考数学圆的切线证明方法

中考数学圆的切线证明方法

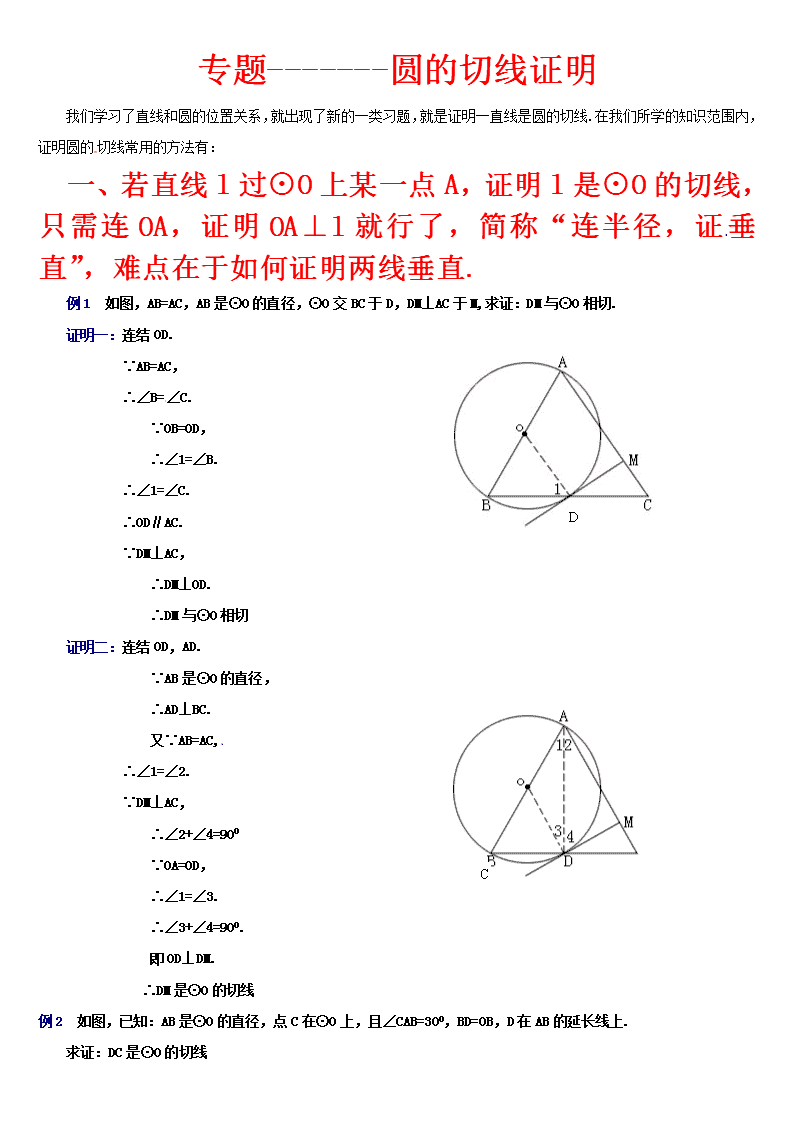
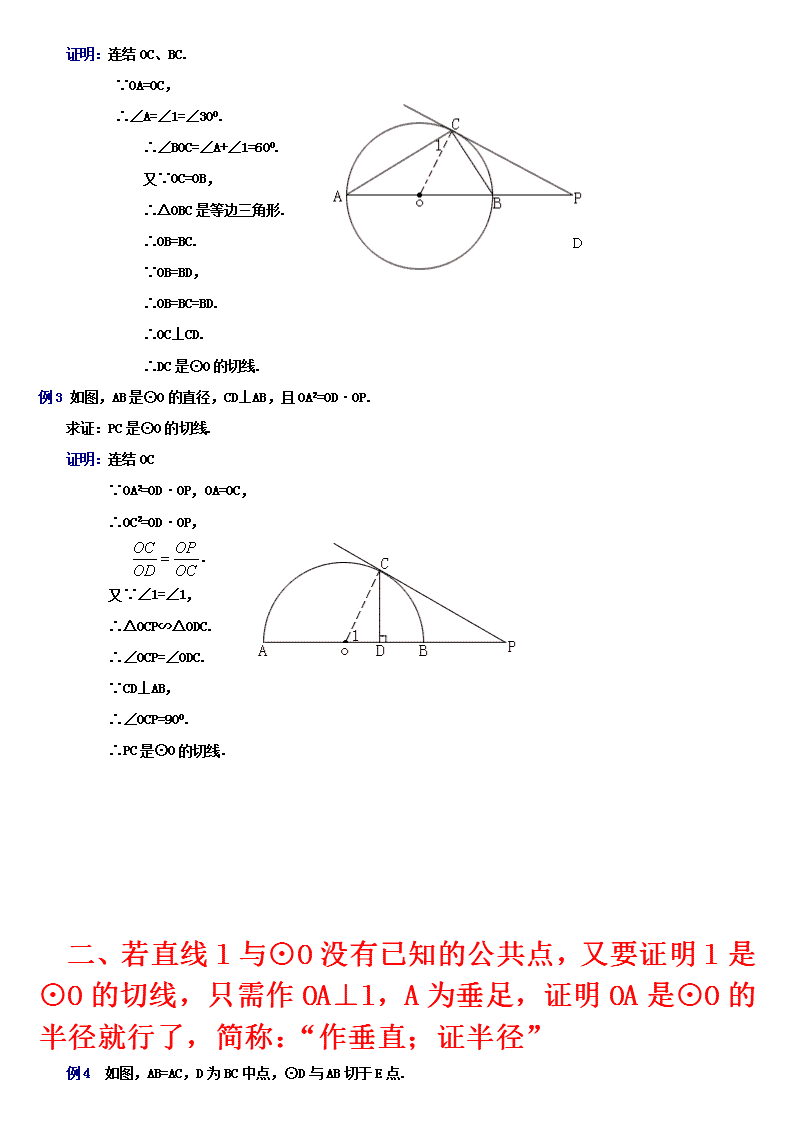
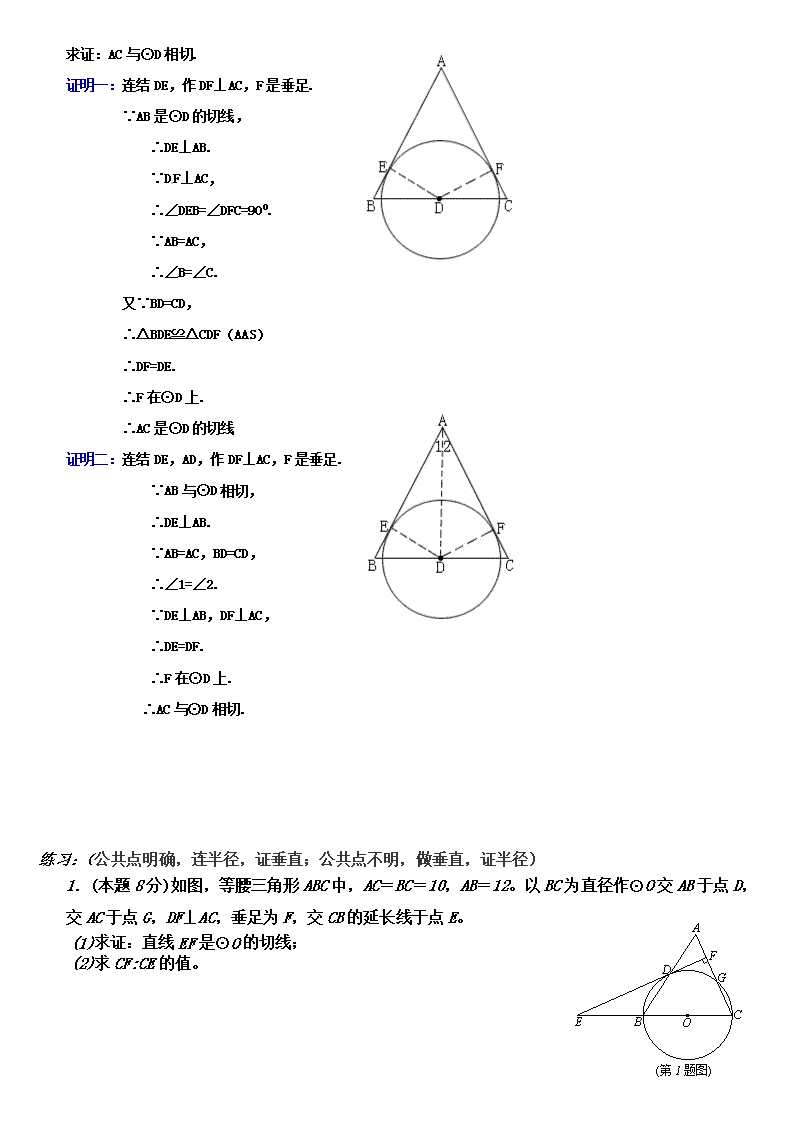
专题-------圆的切线证明 我们学习了直线和圆的位置关系，就出现了新的一类习题，就是证明一直线是圆的切线.在我们所学的知识范围内，证明圆的切线常用的方法有：‎ 一、若直线l过⊙O上某一点A，证明l是⊙O的切线，只需连OA，证明OA⊥l就行了，简称“连半径，证垂直”，难点在于如何证明两线垂直.‎ 例1 如图，AB=AC，AB是⊙O的直径，⊙O交BC于D，DM⊥AC于M,求证：DM与⊙O相切.‎ 证明一：连结OD.‎ ‎ ∵AB=AC，‎ ‎ ∴∠B=∠C.‎ ‎ ∵OB=OD，‎ ‎ ∴∠1=∠B.‎ D ‎ ∴∠1=∠C.‎ ‎ ∴OD∥AC.‎ ‎ ∵DM⊥AC，‎ ‎ ∴DM⊥OD.‎ ‎ ∴DM与⊙O相切 证明二：连结OD，AD.‎ ‎ ∵AB是⊙O的直径，‎ ‎ ∴AD⊥BC.‎ ‎ 又∵AB=AC,‎ ‎ ∴∠1=∠2.‎ ‎ ∵DM⊥AC，‎ ‎ ∴∠2+∠4=900‎ C ‎ ∵OA=OD，‎ ‎ ∴∠1=∠3.‎ ‎ ∴∠3+∠4=900.‎ ‎ 即OD⊥DM. ‎ ‎∴DM是⊙O的切线 例2 如图，已知：AB是⊙O的直径，点C在⊙O上，且∠CAB=300，BD=OB，D在AB的延长线上.‎ 求证：DC是⊙O的切线 证明：连结OC、BC.‎ ‎ ∵OA=OC，‎ ‎ ∴∠A=∠1=∠300.‎ ‎ ∴∠BOC=∠A+∠1=600.‎ ‎ 又∵OC=OB，‎ ‎ ∴△OBC是等边三角形.‎ D ‎ ∴OB=BC.‎ ‎ ∵OB=BD，‎ ‎ ∴OB=BC=BD.‎ ‎ ∴OC⊥CD.‎ ‎ ∴DC是⊙O的切线.‎ 例3 如图，AB是⊙O的直径，CD⊥AB，且OA2=OD·OP.‎ 求证：PC是⊙O的切线.‎ 证明：连结OC ‎ ∵OA2=OD·OP，OA=OC，‎ ‎ ∴OC2=OD·OP，‎ ‎ .‎ ‎ 又∵∠1=∠1，‎ ‎ ∴△OCP∽△ODC.‎ ‎ ∴∠OCP=∠ODC.‎ ‎ ∵CD⊥AB，‎ ‎ ∴∠OCP=900.‎ ‎ ∴PC是⊙O的切线.‎ 二、若直线l与⊙O没有已知的公共点，又要证明l是⊙O的切线，只需作OA⊥l，A为垂足，证明OA是⊙O的半径就行了，简称：“作垂直；证半径”‎ 例4 如图，AB=AC，D为BC中点，⊙D与AB切于E点.‎ 求证：AC与⊙D相切.‎ 证明一：连结DE，作DF⊥AC，F是垂足.‎ ‎ ∵AB是⊙D的切线，‎ ‎ ∴DE⊥AB.‎ ‎ ∵DF⊥AC，‎ ‎ ∴∠DEB=∠DFC=900.‎ ‎ ∵AB=AC，‎ ‎ ∴∠B=∠C.‎ ‎ 又∵BD=CD，‎ ‎ ∴△BDE≌△CDF（AAS）‎ ‎ ∴DF=DE.‎ ‎ ∴F在⊙D上.‎ ‎ ∴AC是⊙D的切线 证明二：连结DE，AD，作DF⊥AC，F是垂足.‎ ‎ ∵AB与⊙D相切，‎ ‎ ∴DE⊥AB.‎ ‎ ∵AB=AC，BD=CD，‎ ‎ ∴∠1=∠2.‎ ‎ ∵DE⊥AB，DF⊥AC，‎ ‎ ∴DE=DF.‎ ‎ ∴F在⊙D上.‎ ‎∴AC与⊙D相切.‎ 练习：（公共点明确，连半径，证垂直；公共点不明，做垂直，证半径）‎ A B D C E F G O ‎(第1题图)‎ ‎1．(本题8分)如图，等腰三角形ABC中，AC＝BC＝10，AB＝12。以BC为直径作⊙O交AB于点D，交AC于点G，DF⊥AC，垂足为F，交CB的延长线于点E。‎ ‎(1)求证：直线EF是⊙O的切线；‎ ‎(2)求CF:CE的值。‎ F E D C B A O ‎2．如图，AB是⊙O的直径，AC是弦，∠BAC的平分线AD交⊙O于点D，DE⊥AC，交AC的延长线于点E，OE交AD于点F．⑴求证：DE是⊙O的切线；⑵若，求的值。‎ ‎3．如图，中，，以为直径作交边于点，是边的中点，连接．‎ ‎（1）求证：直线是的切线；‎ C E B A O F D ‎（2）连接交于点，若，求的值．‎ ‎4．如图，点O在∠APB的平分线上，⊙O与PA相切于点C．‎ ‎ (1) 求证：直线PB与⊙O相切；‎ ‎ (2) PO的延长线与⊙O交于点E．若⊙O的半径为3，PC=4．求弦CE的长．‎