中考数学动点问题专题讲解

中考数学动点问题专题讲解

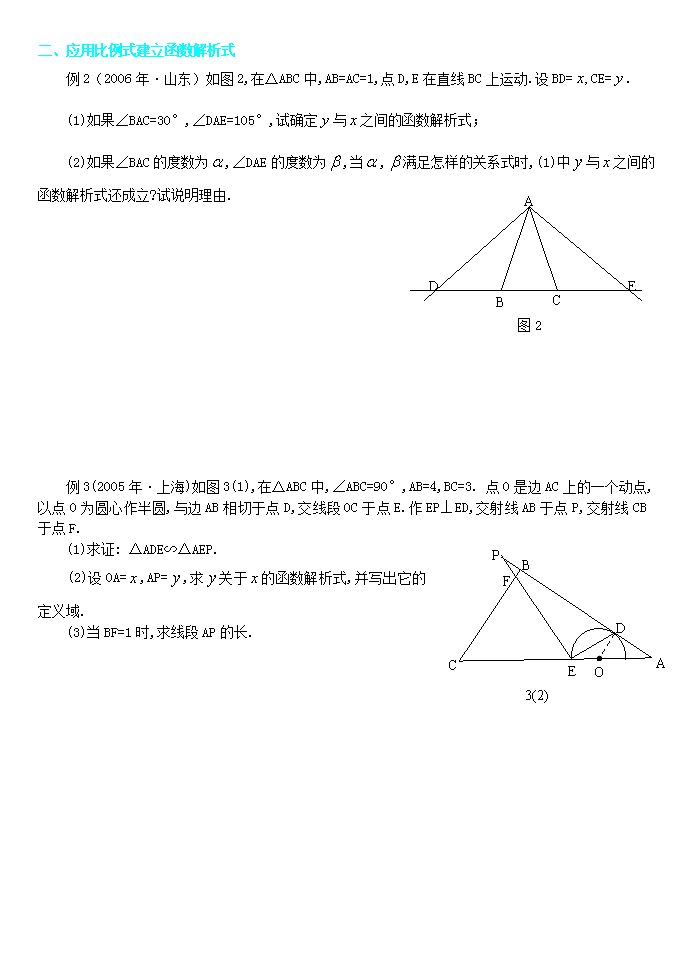
中考动点专题 所谓“动点型问题”是指题设图形中存在一个或多个动点,它们在线段、射线或弧线 上运动的一类开放性题目.解决这类问题的关键是动中求静,灵活运用有关数学知识解决 问题. 关键:动中求静. 数学思想：分类思想 函数思想 方程思想 数形结合思想 转化思想 注重对几何图形运动变化能力的考查 从变换的角度和运动变化来研究三角形、四边形、函数图像等图形，通过“对称、动 点的运动”等研究手段和方法，来探索与发现图形性质及图形变化，在解题过程中渗透空 间观念和合情推理。选择基本的几何图形，让学生经历探索的过程，以能力立意，考查 学生的自主探究能力，促进培养学生解决问题的能力．图形在动点的运动过程中观察图 形的变化情况，需要理解图形在不同位置的情况，才能做好计算推理的过程。在变化中 找到不变的性质是解决数学“动点”探究题的基本思路,这也是动态几何数学问题中最核心 的数学本质。 二期课改后数学卷中的数学压轴性题正逐步转向数形结合、动态几何、动手操作、 实验探究等方向发展．这些压轴题题型繁多、题意创新，目的是考察学生的分析问题、 解决问题的能力，内容包括空间观念、应用意识、推理能力等．从数学思想的层面上讲： （1）运动观点；（2）方程思想；（3）数形结合思想；（4）分类思想；（5）转化思想 等．研究历年来各区的压轴性试题，就能找到今年中考数学试题的热点的形成和命题的 动向，它有利于我们教师在教学中研究对策，把握方向．只的这样，才能更好的培养学 一、应用勾股定理建立函数解析式 例 1(2000 年·上海)如图 1,在半径为 6,圆心角为 90°的扇形 OAB 的弧 AB 上,有一个动点 P,PH ⊥OA,垂足为 H,△OPH 的重心为 G. (1)当点 P 在弧 AB 上运动时,线段 GO、GP、GH 中,有无长度保持不变的线段?如果有,请指出这样 的线段,并求出相应的长度. (2)设 PH x ,GP y ,求 y 关于 x 的函数解析式，并写出函数的定义域(即自变量 x 的取值范围). (3)如果△PGH 是等腰三角形,试求出线段 PH 的长. 二、应用比例式建立函数解析式 HM N G P O A B 图 1 x y 例 2（2006 年·山东）如图 2,在△ABC 中,AB=AC=1,点 D,E 在直线 BC 上运动.设 BD= ,x CE= y . (1)如果∠BAC=30°,∠DAE=105°,试确定 y 与 x 之间的函数解析式； (2)如果∠BAC 的度数为 ,∠DAE 的度数为  ,当 ,  满足怎样的关系式时,(1)中 y 与 x 之间 的函数解析式还成立?试说明理由. 例 3(2005 年·上海)如图 3(1),在△ABC 中,∠ABC=90°,AB=4,BC=3. 点 O 是边 AC 上的一个动点, 以点 O 为圆心作半圆,与边 AB 相切于点 D,交线段 OC 于点 E.作 EP⊥ED,交射线 AB 于点 P,交射线 CB 于 点 F. (1)求证: △ADE∽△AEP. (2)设 OA= x ,AP= y ,求 y 关于 x 的函数解析式,并写出它的 定义域. (3)当 BF=1 时,求线段 AP 的长. 三、应用求图形面积的方法建立函数关系式 例 4（2004 年·上海）如图,在△ABC 中,∠BAC=90°,AB=AC= 22 ,⊙A 的半径为 1.若点 O 在 BC A ED CB 图 2 ● P D E AC B 3(2) O F A F A B C E D 边上运动(与点 B、C 不重合),设 BO= x ,△AOC 的面积为 y . (1)求 y 关于 x 的函数解析式,并写出函数的定义域. (2)以点 O 为圆心,BO 长为半径作圆 O,求当⊙O 与⊙A 相切时, △AOC 的面积. 专题二：动态几何型压轴题 动态几何特点----问题背景是特殊图形，考查问题也是特殊图形，所以要把握好一般与特殊的关 系；分析过程中，特别要关注图形的特性（特殊角、特殊图形的性质、图形的特殊位置。）动点问题 一直是中考热点，近几年考查探究运动中的特殊性：等腰三角形、直角三角形、相似三角形、平行四 边形、梯形、特殊角或其三角函数、线段或面积的最值。下面就此问题的常见题型作简单介绍，解题 方法、关键给以点拨。 一、以动态几何为主线的压轴题 （一）点动问题． 1．（09 年徐汇区）如图， ABC 中， 10 ACAB ， 12BC ，点 D 在边 BC 上，且 4BD ， 以点 D 为顶点作 BEDF  ，分别交边 AB 于点 E ，交射线CA 于点 F ． （1）当 6AE 时，求 AF 的长； （2）当以点 C 为圆心CF 长为半径的⊙C 和以点 A 为圆心 AE 长为半径的⊙ A 相切时， 求 BE 的长； （3）当以边 AC 为直径的⊙O 与线段 DE 相切时，求 BE 的长． [题型背景和区分度测量点] 本题改编自新教材九上《相似形》24.5(4)例六,典型的一 线三角(三等角)问题,试题在原题的基础上改编出第一小题, 当 E 点在 AB 边上运动时，渗透入圆与圆的位置关系(相切 问题)的存在性的研究形成了第二小题,加入直线与圆的位置 关系(相切问题)的存在性的研究形成了第三小题．区分度测 量点在直线与圆的位置关系和圆与圆的位置关系,从而利用 方程思想来求解． [区分度性小题处理手法] 1．直线与圆的相切的存在性的处理方法：利用 d=r 建立方程． 2．圆与圆的位置关系的存在性(相切问题)的处理方法：利用 d=R±r( rR  )建立方程． 3．解题的关键是用含 x 的代数式表示出相关的线段. [ 略解] A B C DE O l A′ A B C DE O l F 解：（1） 证明 CDF ∽ EBD ∴ BE CD BD CF  ，代入数据得 8CF ，∴AF=2 （2） 设 BE= x ,则 ,10 ACd ,10 xAE  利用（1）的方法 xCF 32 ， 相切时分外切和内切两种情况考虑： 外切， xx 321010  ， 24x ； 内切， xx 321010  ， 17210 x ． 100  x ∴当⊙C 和⊙ A 相切时， BE 的长为 24 或 17210  ． （3）当以边 AC 为直径的⊙O 与线段 DE 相切时， 3 20BE ． 类题 ⑴一个动点：09 杨浦 25 题（四月、五月）、09 静安 25 题、 ⑵两个动点：09 闸北 25 题、09 松江 25 题、09 卢湾 25 题、09 青浦 25 题． （二）线动问题 在矩形 ABCD 中，AB＝3，点 O 在对角线 AC 上，直线 l 过点 O，且与 AC 垂直交 AD 于点 E.(1) 若直线 l 过点 B，把△ABE 沿直线 l 翻折，点 A 与矩形 ABCD 的对称中心 A＇重合，求 BC 的长； (2)若直线 l 与 AB 相交于点 F，且 AO＝ 4 1 AC，设 AD 的长为 x ，五边 形 BCDEF 的面积为 S.①求 S 关于 x 的函数关系式，并指出 x 的取值范 围； ②探索：是否存在这样的 x ，以 A 为圆心，以 x 4 3 长为半径的圆与 直线 l 相切，若存在，请求出 x 的值；若不存在，请说明理由． [题型背景和区分度测量点] 本题以矩形为背景,结合轴对称、相似、三角等相关知识编制得到．第 一小题考核了学生轴对称、矩形、勾股定理三小块知识内容；当直线l 沿 AB 边向上平移时，探求面积函数解析式为区分测量点一、加入直线与圆 的位置关系(相切问题)的存在性的研究形成了区分度测量点二． [区分度性小题处理手法] 1．找面积关系的函数解析式，规则图形套用公式或用割补法，不规 则图形用割补法． 2．直线与圆的相切的存在性的处理方法：利用 d=r 建立方程． 3．解题的关键是用含 x 的代数式表示出相关的线段. [ 略解] (1)∵A’是矩形 ABCD 的对称中心∴A’B＝AA’＝ 2 1 AC ∵AB＝A’B，AB＝3∴AC＝6 33BC (2)① 92  xAC ， 94 1 2  xAO ， )9(12 1 2  xAF ， x xAE 4 92  ∴ AF2 1  AES AEF x x 96 )9( 22  ， x xxS 96 )9(3 22  x xxS 96 81270 24  ( 333  x ) ②若圆 A 与直线 l 相切，则 94 1 4 3 2  xx ， 01 x (舍去)， 5 8 2 x ∵ 35 8 2 x ∴不存在这样的 x ，使圆 A 与直线 l 相切． [类题]09 虹口 25 题． （三）面动问题 如图，在 ABC 中， 6,5  BCACAB ， D 、 E 分别是边 AB 、 AC 上 的两个动点（ D 不与 A 、B 重合），且保持 BCDE ∥ ，以 DE 为边，在点 A 的异侧作正方形 DEFG . （1）试求 ABC 的面积； （2）当边 FG 与 BC 重合时，求正方形 DEFG 的边长； （3）设 xAD  ， ABC 与正方形 DEFG 重叠部分的面积为 y ，试求 y 关 于 x 的函数关系式，并写出定义域； （4）当 BDG 是等腰三角形时，请直接写出 AD 的长． [题型背景和区分度测量点] 本题改编自新教材九上《相似形》24.5(4)例七,典型的共角相似三角形问题,试题为了形成坡度， 在原题的基础上改编出求等腰三角形面积的第一小题,当 D 点在 AB 边上运动时，正方形 DEFG 整体 动起来，GF 边落在 BC 边上时，恰好和教材中的例题对应，可以说是相似三角形对应的小高比大高= 对应的小边比大边，探寻正方形和三角形的重叠部分的面积与线段 AD 的关系的函数解析式形成了第 三小题，仍然属于面积类习题来设置区分测量点一，用等腰三角形的存在性来设置区分测量点二． [区分度性小题处理手法] 图3-5 图3-4 图3-3 图3-2 图3-1 K F G E K F G E F G E U K F G E F G E C A A C A C A C A C B D B D B D B D B D 1．找到三角形与正方形的重叠部分是解决本题的关键，如上图 3-1、3-2 重叠部分分别为正方形 和矩形包括两种情况． 2．正确的抓住等腰三角形的腰与底的分类，如上图 3-3、3-4、3-5 用方程思想解决． 3．解题的关键是用含 x 的代数式表示出相关的线段. [ 略解] 解：（1） 12ABCS . F G E C A B D （2）令此时正方形的边长为 a ，则 4 4 6 aa  ，解得 5 12a . （3）当 20 x 时， 2 2 25 36 5 6 xxy      ， 当 52  x 时，   2 25 24 5 2455 4 5 6 xxxxy  . （4） 7 20,11 25,73 125AD . [类题] 改编自 09 奉贤 3 月考 25 题，将条件（2）“当点 M、N 分别在边 BA、CA 上时”,去掉，同 时加到第（3）题中. 已知：在△ABC 中，AB=AC，∠B=30º，BC=6，点 D 在边 BC 上，点 E 在线段 DC 上，DE=3，△DEF 是等边三角形，边 DF、EF 与边 BA、CA 分别相交于点 M、N． （1）求证：△BDM∽△CEN； （2）设 BD= x ，△ABC 与△DEF 重叠部分的面积为 y ，求 y 关于 x 的函数解析式，并写出定义域． （3）当点 M、N 分别在边 BA、CA 上时,是否存在点 D，使以 M 为圆心, BM 为半径的圆与直线 EF 相切, 如果存在，请求出 x 的值；如不存在，请说明理由． 例 1：已知⊙O 的弦 AB 的长等于⊙O 的半径，点 C 在⊙O 上变化（不与 A、B）重合，求∠ACB 的大小 . 分析：点 C 的变化是否影响∠ACB 的大小的变化呢?我们不妨将点 C 改变一下,如何变化呢？可 能在优弧 AB 上，也可能在劣弧 AB 上变化，显然这两者的结果不一样。那么，当点 C 在优弧 AB 上 变化时，∠ACB 所对的弧是劣弧 AB，它的大小为劣弧 AB 的一半，因此很自然地想到它的圆心角， 连结 AO、BO，则由于 AB=OA=OB，即三角形 ABC 为等边三角形，则∠AOB=600，则由同弧所对 的圆心角与圆周角的关系得出：∠ACB= 2 1 ∠AOB=300， 当点 C 在劣弧 AB 上变化时，∠ACB 所对的弧是优弧 AB，它的大小为优弧 AB 的一半，由∠ AOB=600 得，优弧 AB 的度数为 3600-600=3000，则由同弧所对的圆心角与 圆周角的关系得出：∠ACB=1500， 因此，本题的答案有两个，分别为 300 或 1500. 反思：本题通过点 C 在圆上运动的不确定性而引起结果的不唯一性。从 而需要分类讨论。这样由点 C 的运动变化性而引起的分类讨论在解题中经常 出现。 变式 1：已知△ABC 是半径为 2 的圆内接三角形，若 32AB ，求∠C 的 大小. A B F D E M N C O B A C O B A C 本题与例 1 的区别只是 AB 与圆的半径的关系发生了一些变化,其解题方法与上面一致,在三角形 AOB 中, 2 32 1 2 1sin  OB AB AOB ,则 0602 1 AOB ,即 0120AOB , 从而当点 C 在优弧 AB 上变化时，∠C 所对的弧是劣弧 AB，它的大小为劣弧 AB 的一半，即 060C , 当点 C 在劣弧 AB 上变化时，∠C 所对的弧是优弧 AB，它的大小为优 弧 AB 的一半，由∠AOB=1200 得，优弧 AB 的度数为 3600-1200=2400，则 由同弧所对的圆心角与圆周角的关系得出：∠C=1200， 因此 060C 或∠C=1200. 变式 2: 如图,半经为 1 的半圆 O 上有两个动点 A、B，若 AB=1， 判断∠AOB 的大小是否会随点 A、B 的变化而变化，若变化，求出变化范 围，若不变化，求出它的值。 四边形 ABCD 的面积的最大值。 解：（1）由于 AB=OA=OB，所以三角形 AOB 为等边三角形，则∠ AOB=600，即∠AOB 的大小不会随点 A、B 的变化而变化。 （2）四边形 ABCD 的面积由三个三角形组成，其中三角形 AOB 的面积为 4 3 ，而三角 形 AOD 与三角形 BOC 的面积之和为 )(2 1 2 1 2 1 BGAFBGOCAFOD  ，又由梯形 的中位线定理得三角形 AOD 与三角形 BOC 的面积之和 EHBGAF  )(2 1 ，要四边形 ABCD 的面积最大，只需 EH 最大，显然 EH≤OE= 2 3 ，当 AB∥CD 时，EH=OE，因此 四边形 ABCD 的面积最大值为 4 3 + 2 3 = 4 33 . 对于本题同学们还可以继续思考:四边形 ABCD 的周长的变化范围. 变式 3: 如图,有一块半圆形的木板,现要把它截成三角形板块.三角形的 两个顶点分 别为 A、B，另一个顶点 C 在半圆上，问怎样截取才能使截出的三角形 的面积最大？要求说明理由（广州市 2000 年考题） 分析：要使三角形 ABC 的面积最大，而三角形 ABC 的底边 AB 为 圆的直径为常量，只需 AB 边上的高最大即可。过点 C 作 CD⊥AB 于点 D，连结 CO， 由于 CD≤CO，当 O 与 D 重合，CD=CO，因此，当 CO 与 AB 垂直时， H G F E O D C B A A B C D O O C B A D A B C O 即 C 为半圆弧 的中点时，其三角形 ABC 的面积最大。 本题也可以先猜想，点 C 为半圆弧的中点时，三角形 ABC 的面积最大，故只需另选一个位置 C1（不 与 C 重合），，证明三角形 ABC 的面积大于三角形 ABC1 的面积即可。如图 显然三角形 ABC1 的面积= 2 1 AB×C1D，而 C1D< C1O=CO,则三角形 ABC1 的面积= 2 1 AB× C1D< 2 1 AB×C1O=三角形 ABC 的面积,因此,对于除点 C 外的任意点 C1,都有三角形 ABC1 的面积小 于三角形三角形 ABC 的面积,故点 C 为半圆中点时,三角形 ABC 面积最大. 本题还可研究三角形 ABC 的周长何时最大的问题。 提示：利用周长与面积之间的关系。要三角形 ABC 的周长最大，AB 为常 数，只需 AC+BC 最大，而（AC+BC）2=AC2+CB2+2AC×BC=AB2+4× ΔABC 的面积，因此ΔABC 的面积最大时，AC+BC 最大，从而ΔABC 的周长最大。 从以上一道题及其三个变式的研究我们不难发现,解决动态几何问题的常 见方法有: 一、 特殊探路，一般推证 例 2：（2004 年广州市中考题第 11 题）如图，⊙O1 和⊙O2 内切于 A，⊙O1 的半径为 3，⊙O2 的半径为 2，点 P 为⊙O1 上的任一点（与点 A 不重合），直线 PA 交⊙O2 于点 C，PB 切⊙O2 于点 B，则 PC BP 的值为 （A） 2 （B） 3 （C） 2 3 （D） 2 6 分析：本题是一道选择题，给出四个答案有且只有一个是正确的，因此可以 取一个特殊位置进行研究，当点 P 满足 PB⊥AB 时，可以通过计算得出 PB= 2213 22  BC×AP=BP×AB，因此 BC= 6 24 62 28 816 28 22      BPAB BPAB ， 在三角形 BPC 中，PC= 3 6222  BCBP ， 所以， PC BP = 3 选（B） C D A B C 1 O C O 1 O 2 P B A C O 1 O 2 P B A 当然，本题还可以根据三角形相似得 BP AP PC BP  ，即可计算出结论。 作为一道选择题，到此已经完成，但如果是一道解答题，我们得出的结论只是一个特殊情况，还要进 一步证明对一般情况也成立。 例 3：如图，在等腰直角三角形 ABC 中，斜边 BC=4，OA  BC 于 O,点 E 和点 F 分别在边 AB、AC 上滑动并保持 AE=CF,但点 F 不与 A、C 重合，点 E 不与 B、A 重合。 判断  OEF 的形状，并加以证明。 判断四边形 AEOF 的面积是否随点 E、F 的变化而变化，若变化， 求其变化范围，若不变化，求它的值.  AEF 的面积是否随着点 E、F 的变化而变化，若变化，求其变 化范围，若不变化，求它的值。 分析：本题结论很难发现，先从特殊情况入手。最特殊情况为 E、F 分别为 AB、AC 中点，显然有Δ EOF 为等腰直角三角形。还可发现当点 E 与 A 无限接近时，点 F 与点 C 无 限接近，此时ΔEOF 无限接近ΔAOC，而ΔAOC 为等腰直角三角形，几种 特殊情况都可以得出ΔEOF 为等腰直角三角形。一般情况下成立吗？OE 与 OF 相等吗？∠EOF 为直角吗？能否证明。如果它们成立，便可以推出三角 形 OFC 与三角形 OEA 全等，一般情况下这两个三角形全等吗？ 不难从题目的条件可得：OA=OC，∠OCF=∠OAE，而 AE=CF，则ΔOEA ≌ΔOFC，则 OE=OF，且∠FOC=∠EOA，所以∠EOF=∠EOA+∠AOF=∠ FOC+∠FOA=900，则∠EOF 为直角，故ΔEOF 为等腰直角三角形。 二、 动手实践，操作确认 例 4（2003 年广州市中考试题）在⊙O 中，C 为弧 AB 的中点，D 为弧 AC 上任一点（与 A、C 不重合），则 （A）AC+CB=AD+DB (B) AC+CBAD+DB (D) AC+CB 与 AD+DB 的大小关系不确定 分析:本题可以通过动手操作一下,度量 AC、CB、AD、DB 的长度，可以尝试换几个位置量一量， 得出结论（C） 例 5：如图，过两同心圆的小圆上任一点 C 分别作小圆的直径 CA 和非直径的弦 CD，延长 CA 和 CD 与大圆分别交于点 B、E，则下列结论中正确的是（ * ） （A） ABDE  （B） ABDE  （C） ABDE  （D） ABDE, 的大小不确定 分析：本题可以通过度量的方法进行，选（B） 本题也可以可以证明得出结论，连结 DO、EO，则在三角形 OED 中， 由于两边之差小于第三边，则 OE—OD3).动点 M，N 同时从 B 点出发，分别沿 B→A，B→C 运动，速度是 1 厘米/秒.过 M 作直线垂直于 AB，分别交 AN，CD 于 P，Q.当点 N 到达终点 C 时，点 M 也随之停止运动.设运动时间为 t 秒. (1)若 a=4 厘米，t=1 秒，则 PM=厘米； (2)若 a=5 厘米，求时间 t，使△PNB∽△PAD，并求出它们的相似比； (3)若在运动过程中，存在某时刻使梯形 PMBN 与梯形 PQDA 的面积相等，求 a 的取值范围； (4)是否存在这样的矩形：在运动过程中，存在某时刻使梯形 PMBN，梯形 PQDA，梯形 PQCN 的面积都相等?若存在，求 a 的值；若不存在，请说明理由. 评析 本题是以双动点为载体，矩形为背景创设的存在性问题.试题由浅入深、层层递进，将几何 与代数知识完美的综合为一题，侧重对相似和梯形面积等知识点的考查，本题的难点主要是题(3)，解 决此题的关键是运用相似三角形的性质用 t 的代数式表示 PM，进而利用梯形面积相等列等式求出 t 与 a 的函数关系式，再利用 t 的范围确定的 a 取值范围. 第(4)小题是题(3)结论的拓展应用，在解决此 问题的过程中，要有全局观念以及对问题的整体把握. 4 以双动点为载体，探求函数最值问题 例 4 (2007 年吉林省)如图 9，在边长为 82cm 的正方形 ABCD 中，E、F 是对角线 AC 上的两个 动点，它们分别从点 A、C 同时出发，沿对角线以 1cm/s 的相同速度运动，过 E 作 EH 垂直 AC 交 Rt△ACD 的直角边于 H；过 F 作 FG 垂直 AC 交 Rt△ACD 的直角边于 G，连结 HG、EB.设 HE、EF、 FG、GH 围成的图形面积为 S 1，AE、EB、BA 围成的图形面积为 S 2(这里规定：线段的面积为 0).E 到达 C，F 到达 A 停止.若 E 的运动时间为 x(s)，解答下列问题： (1)当 0

查看更多