中考尺规作图复习讲义

中考尺规作图复习讲义

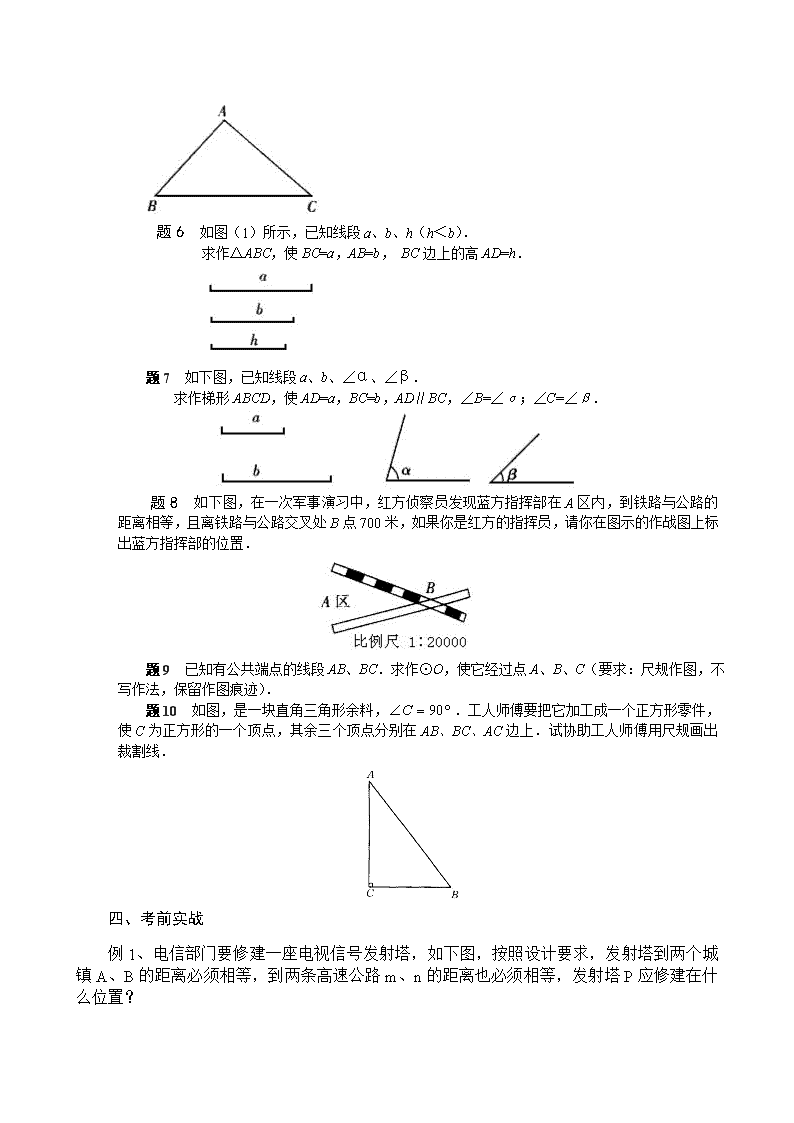
中考尺规作图复习讲义 一、 定义：‎ 在几何中，我们把只限定用直尺（无刻度）和圆规来画图的方法，称为尺规作图．其中直尺只能用来作直线、线段、射线或延长线段；圆规用来作圆和圆弧．由此可知，尺规作图与一般的画图不同，一般画图可以动用一切画图工具，包括三角尺、量角器等，在操作过程中可以度量，但尺规作图在操作过程中是不允许度量成分的．‎ 二、 中考需要掌握的尺规作图部分有如下的要求：‎ 1. 完成以下基本作图：①作一条线段等于已知线段②作一个角等于已知角③作已知角的平分线④作线段的垂直平分线⑤过一点做已知直线的垂线。‎ 2. 利用基本作图作三角形：已知三边作三角形；已知两边及其夹角作三角形；已知两角及其夹边作三角形；已知底边及底边上的高作等腰三角形;已知一直角边和斜边作直角三角形。‎ 3. 探索如何过一点、两点和不在同一直线上的三点作圆．‎ 4. 了解作图原理，保留作图痕迹，不要求写作法。‎ 我们在掌握这些方法的基础上，还应该会解一些新颖的作图题，进一步培养形象思维能力．与传统的尺规作图相比，作图题试题开放，联系实际，要求学生进行多方位，多角度，多层次的探究，考查了学生思维的灵活性，发散性，创新性。‎ 三、 典型题目 题① 已知线段a、b，画一条线段，使其等于． ‎ ‎② 已知线段a和b，求作一条线段AD使它的长度等于2a－b．‎ 题2 如下图，已知∠α及线段a，求作等腰三角形，使它的底角为α，底边为a．‎ 题3 已知直线AB及直线AB外一点C，过点C作CD∥AB（写出作法，画出图形）．‎ ‎ 题4 如下图，△ABC中，a=5cm，b=3cm，c=3.5cm，∠B=，∠C=，请你从中选择适当的数据，画出与△ABC全等的三角形（把你能画的三角形全部画出来，不写画法但要在所画的三角形中标出用到的数据）． ‎ 题5 正在修建的中山北路有一形状如下图所示的三角形空地需要绿化．拟从点A出发，将△ABC分成面积相等的三个三角形，以便种上三种不同的花草，请你帮助规划出图案（保留作图痕迹，不写作法）．‎ 题6 如图（1）所示，已知线段a、b、h（h＜b）．‎ 求作△ABC，使BC=a，AB=b， BC边上的高AD=h．‎ 题7 如下图，已知线段a、b、∠α、∠β．‎ 求作梯形ABCD，使AD=a，BC=b，AD∥BC，∠B=∠α；∠C=∠β．‎ 题8 如下图，在一次军事演习中，红方侦察员发现蓝方指挥部在A区内，到铁路与公路的距离相等，且离铁路与公路交叉处B点700米，如果你是红方的指挥员，请你在图示的作战图上标出蓝方指挥部的位置．‎ 题9 已知有公共端点的线段AB、BC．求作⊙O，使它经过点A、B、C（要求：尺规作图，不写作法，保留作图痕迹）．‎ 题10 如图，是一块直角三角形余料，．工人师傅要把它加工成一个正方形零件，使C为正方形的一个顶点，其余三个顶点分别在AB、BC、AC边上．试协助工人师傅用尺规画出裁割线．‎ 四、考前实战 例1、‎ 电信部门要修建一座电视信号发射塔，如下图，按照设计要求，发射塔到两个城镇A、B的距离必须相等，到两条高速公路m、n的距离也必须相等，发射塔P应修建在什么位置？ 　 　【分析】 这是一道实际应用题，关键是转化成数学问题，根据题意知道，点P应满足两个条件，一是在线段AB的垂直平分线上；二是在两条公路夹角的平分线上，所以点P应是它们的交点. 　解：（1）作两条公路夹角的平分线OC； 　（2）作线段AB的垂直平分线EF；则射线OC与直线EF的交点P就是发射塔的位置. 　 例2、 在平面直角坐标系中，点A的坐标是（4，0），O是坐标原点，在直线y=x+3上求一点P，使△AOP是等腰三角形，这样的P点有几个？ 　【分析】 首先要清楚点P需满足两个条件，一是点P在y=x+3上；二是△AOP必须是等腰三角形. 　其次，寻找P点要分情况讨论，也就是当OA=OP时，以O点为圆心，OA为半径画圆，与直线有两交点P1、P2；当OA=AP时，以A点为圆心，OA为半径画圆，与直线有两交点P3、P4；当PO=PA时，作OA的垂直平分线，与直线有一交点P5，所以总计这样的P点有五个 　 ‎ ‎【例3】（贵阳市）如图，现有，两堵墙，两个同学分别站在A处和B处，请问小明在哪个区域内活动才不会同时被这两个同学发现（画图用阴影表示）。‎ 分析：小明在阴影部分的区域就不会同时发现。‎ ‎【例4】（河北省）如图，晚上，小亮在广场上乘凉。图中线段AB表示站立在广场上的小亮，线段PO表示直立在广场上的灯杆，点P表示照明灯。（1）请你在图中画出小亮在照灯（P）照射下的影子；（2）如果灯杆高PO=‎12m，小亮的身高AB=‎1.6m，小亮下与灯杆的距离BO=‎13m，请求出小亮影子的长度。‎ 解析：在△CAB和△CPO中，∵∠B=∠C,∠ABC=POC=900, ∴△CAB∽△CPO ‎∴ ‎ ‎∴BC=2 ‎ ‎∴小亮的影子长为‎2m.‎ A B C ‎【例5】为美化校园，学校准备在如图所示的三角形（△ABC）空地上修建一个面积最大的圆形花坛，请在图中画出这个圆形花坛．‎ ‎【例6】（2015•陕西）如图，已知△ABC，请用尺规过点A作一条直线，使其将△ABC分成面积相等的两部分．（保留作图痕迹，不写作法）‎ ‎【例7】（贵阳市）在一次数学探究活动中，小强用两条直线把平行四边形ABCD分割成四个部分，使含有一组对顶角的两个图形全等。‎ ‎（1）根据小强的分割方法，你认为把平等四边形分割成满足以上全等关系的直线有 组；‎ ‎（2）请在图中的三个平行四边形中画出满足小强分割方法的直线；‎ ‎（3）由上述实验操作过程，你发现所画的两条直线有什么规律？‎ 解析：无数，这两条直线经过平行四边形的对称中心，‎ ‎【例8】（宁夏回族自治区）在下面网格中，每个小正方形的边长均为1，请你画出以格点为顶点，面积为10个平方单位的等腰三角形，在给出的网格中画出两个既符合条件且不全等的三角形（所画的两个三角形若全等视为一个）。‎ ‎【例9】（2015•酒泉第21题 6分）如图，已知在△ABC中，∠A=90°‎ ‎（1）请用圆规和直尺作出⊙P，使圆心P在AC边上，且与AB，BC两边都相切（保留作图痕迹，不写作法和证明）．‎ ‎（2）若∠B=60°，AB=3，求⊙P的面积．‎