中考数学专题复习十 圆练习

中考数学专题复习十 圆练习

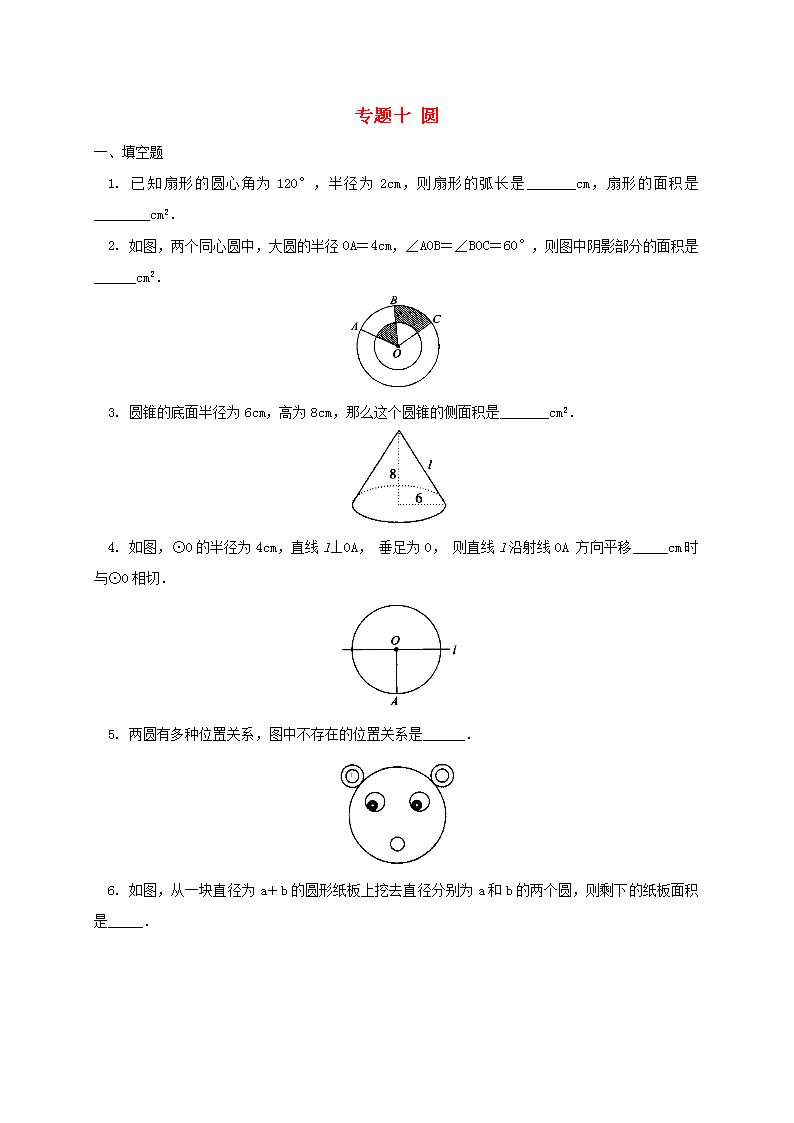
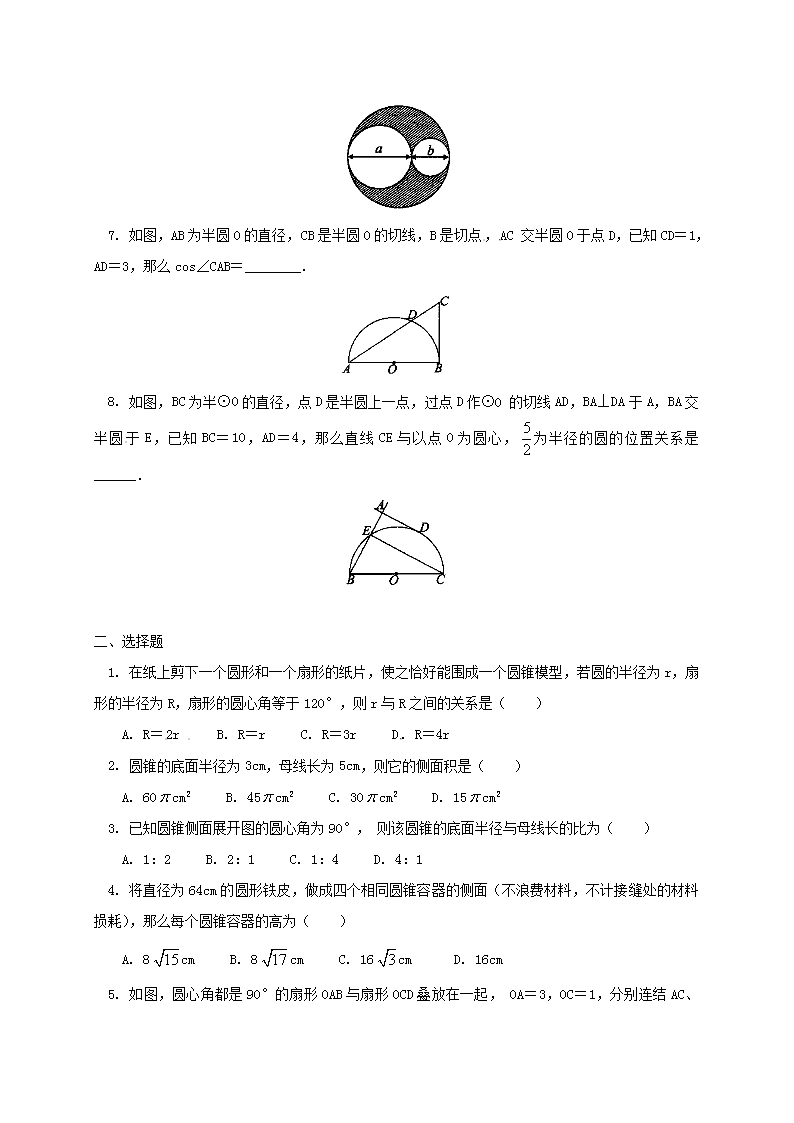
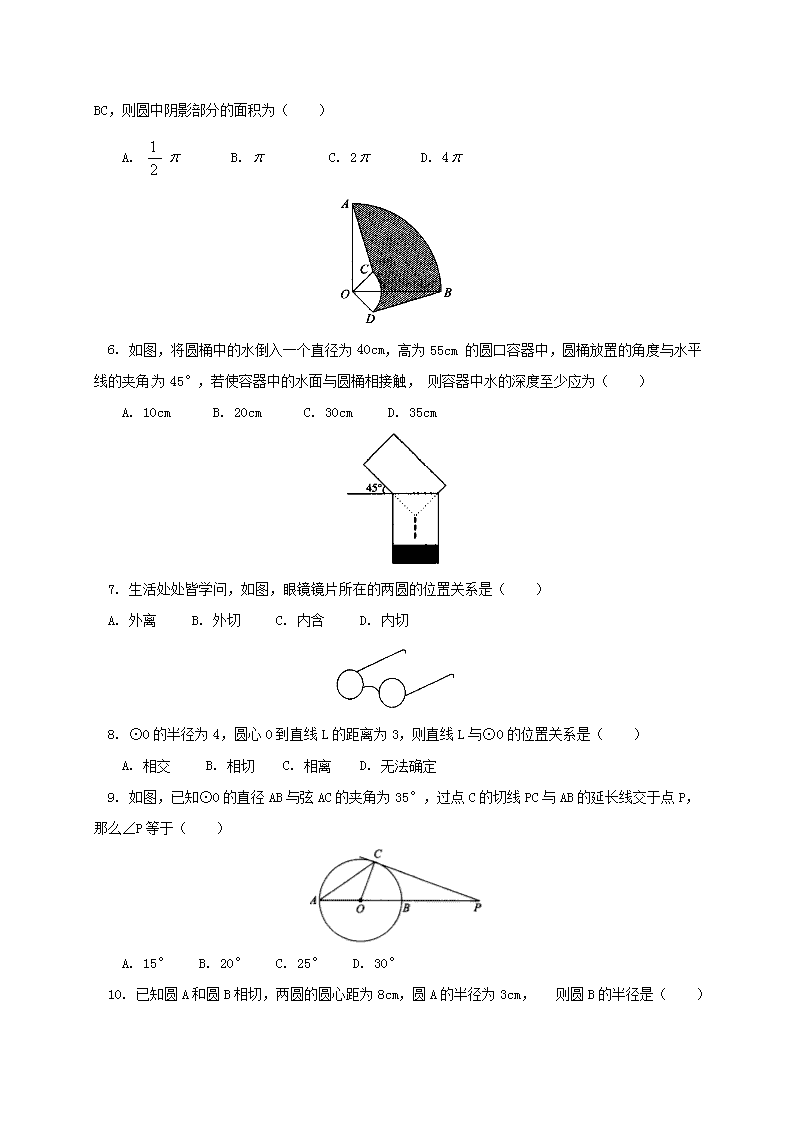
专题十 圆 一、填空题 ‎1. 已知扇形的圆心角为120°，半径为‎2cm，则扇形的弧长是_______cm，扇形的面积是________cm2．‎ ‎2. 如图，两个同心圆中，大圆的半径OA＝‎4cm，∠AOB＝∠BOC＝60°，则图中阴影部分的面积是______cm2．‎ ‎3. 圆锥的底面半径为‎6cm，高为‎8cm，那么这个圆锥的侧面积是_______cm2．‎ ‎4. 如图，⊙O的半径为‎4cm，直线l⊥OA，垂足为O，则直线l沿射线OA方向平移_____cm时与⊙O相切． ‎ ‎5. 两圆有多种位置关系，图中不存在的位置关系是______．‎ ‎6. 如图，从一块直径为a＋b的圆形纸板上挖去直径分别为a和b的两个圆，则剩下的纸板面积是_____．‎ ‎7. 如图，AB为半圆O的直径，CB是半圆O的切线，B是切点，AC交半圆O于点D，已知CD＝1，AD＝3，那么cos∠CAB＝________．‎ ‎8. 如图，BC为半⊙O的直径，点D是半圆上一点，过点D作⊙O的切线AD，BA⊥DA于A，BA交半圆于E，已知BC＝10，AD＝4，那么直线CE与以点O为圆心，为半径的圆的位置关系是______．‎ 二、选择题 ‎1. 在纸上剪下一个圆形和一个扇形的纸片，使之恰好能围成一个圆锥模型，若圆的半径为r，扇形的半径为R，扇形的圆心角等于120°，则r与R之间的关系是（ ）‎ ‎ A. R＝2r B. R＝r C. R＝3r D. R＝4r ‎2. 圆锥的底面半径为‎3cm，母线长为‎5cm，则它的侧面积是（ ）‎ ‎ A. 60cm2 B. 45cm‎2 C. 30cm2 D. 15cm2‎ ‎3. 已知圆锥侧面展开图的圆心角为90°，则该圆锥的底面半径与母线长的比为（ ）‎ ‎ A. 1：2 B. 2：‎1 C. 1：4 D. 4：1‎ ‎4. 将直径为‎64cm的圆形铁皮，做成四个相同圆锥容器的侧面（不浪费材料，不计接缝处的材料损耗），那么每个圆锥容器的高为（ ）‎ ‎ A. 8cm B. 8cm C. 16cm D. ‎‎16cm ‎5. ‎ 如图，圆心角都是90°的扇形OAB与扇形OCD叠放在一起，OA＝3，OC＝1，分别连结AC、BC，则圆中阴影部分的面积为（ ）‎ A. B. C. 2 D. 4‎ ‎6. 如图，将圆桶中的水倒入一个直径为‎40cm，高为‎55cm的圆口容器中，圆桶放置的角度与水平线的夹角为45°，若使容器中的水面与圆桶相接触，则容器中水的深度至少应为（ ）‎ ‎ A. ‎10cm B. ‎20cm C. ‎30cm D. ‎‎35cm ‎7. 生活处处皆学问，如图，眼镜镜片所在的两圆的位置关系是（ ）‎ A. 外离 B. 外切 C. 内含 D. 内切 ‎8. ⊙O的半径为4，圆心O到直线L的距离为3，则直线L与⊙O的位置关系是（ ）‎ ‎ A. 相交 B. 相切 C. 相离 D. 无法确定 ‎9. 如图，已知⊙O的直径AB与弦AC的夹角为35°，过点C的切线PC与AB的延长线交于点P，那么∠P等于（ ）‎ ‎ A. 15° B. 20° C. 25° D. 30°‎ ‎10. 已知圆A和圆B相切，两圆的圆心距为‎8cm，圆A的半径为‎3cm， 则圆B的半径是（ ）‎ ‎ A. ‎5cm B. ‎11cm C. ‎3cm D. ‎5cm或‎11cm ‎11. 如图PB为⊙O的切线，B为切点，连结PO交⊙O于点A，PA＝2，PO＝5，则PB的长度为（ ）‎ A. 4 B. C. 2 D. 4‎ ‎12. 如图，AB与⊙O切于点B，AO＝‎6cm，AB＝‎4cm，则⊙O的半径为（ ）‎ A. 4cm B. ‎2cm C. 2cm D. m 三、解答题 ‎1. 如图，已知正三角形ABC的边长为‎2a．‎ ‎ （1）求它的内切圆与外接圆组成的圆环的面积．‎ ‎ （2）根据计算结果，要求圆环的面积，只需测量哪一条弦的大小就可算出圆环的面积；‎ ‎ （3）将条件中的“正三角形”改为“正方形”“正六边形”，你能得出怎样的结论？‎ ‎ （4）已知正n边形的边长为‎2a，请写出它的内切圆与外接圆组成的圆环面积．‎ ‎2. 如图，已知O为原点，点A的坐标为（4，3），⊙A的半径为2. 过A作直线平行于轴，点P在直线上运动．‎ ‎（1）当点P在⊙A上时，请你直接写出它的坐标；‎ ‎（2）设点P的横坐标为12，试判断直线OP与⊙A的位置关系，并说明理由．‎ ‎3. 如图1，已知中，，．过点作，且，连接交于点．‎ ‎（1）求的长；‎ ‎（2）以点为圆心，为半径作⊙A，试判断与⊙A是否相切，并说明理由；‎ ‎（3）如图2，过点作，垂足为．以点为圆心，为半径作⊙A；以点为圆心，为半径作⊙C．若和的大小是可变化的，并且在变化过程中保持⊙A和⊙C相切，且使点在⊙A的内部，点在⊙A的外部，求和的变化范围．‎ ‎4. 已知：AB为⊙O的直径，P为AB弧的中点．‎ ‎（1）若⊙O′与⊙O外切于点P（见图甲），AP、BP的延长线分别交⊙O′于点C、D，连接CD，则△PCD是 三角形； ‎ （2）若⊙O′与⊙O相交于点P、Q（见图乙），连接AQ、BQ并延长分别交⊙O′于点E、F，请选择下列两个问题中的一个作答：‎ 问题一：判断△PEF的形状，并证明你的结论；‎ 问题二：判断线段AE与BF的关系，并证明你的结论．‎ ‎ 我选择问题 ，结论： .‎ ‎5. 从卫生纸的包装纸上得到以下资料：两层300格，每格‎11.4cm×‎11cm，如图甲。用尺量出整卷卫生纸的半径（）与纸筒内芯的半径（），分别为‎5.8cm和‎2.3cm，如图乙。那么该两层卫生纸的厚度为多少cm？（π取3.14，结果精确到‎0.001cm）‎ ‎6. 设边长为‎2a的正方形的中心A在直线l上，它的一组对边垂直于直线l，半径为r的⊙O的圆心O在直线l上运动，点A、O间距离为D．‎ ‎（1）如图①，当r＜a时，根据d与a、r之间的关系，将⊙O与正方形的公共点的个数填入下表：‎ d、a、r之间的关系 公共点的个数 d＞a＋r d＝a＋r a－r＜d＜a＋r d＝a－r d＜a－r 所以，当r＜a时，⊙O与正方形的公共点的个数可能有　　　　　　　　　个；‎ ‎（2）如图②，当r＝a时，根据d与a、r之间的关系，将⊙O与正方形的公共点的个数填入下表：‎ d、a、r之间的关系 公共点的个数 d＞a＋r d＝a＋r a≤d＜a＋r d＜a 所以，当r＝a时，⊙O与正方形的公共点的个数可能有　　　　　　　　个；‎ ‎（3）如图③，当⊙O与正方形有5个公共点时，试说明r＝a；‎ ‎（4）就r＞a的情形，请你仿照“当……时，‎ ‎⊙O与正方形的公共点的个数可能有 个”的形式，至少给出一个关于“⊙O与正方形的公共点的个数”的正确结论．‎ 练习答案 一、填空题 ‎1. ， 2. 3. 60‎ ‎4. 4 5. 两圆相交 6. ‎ ‎7. 8. 相离 二、选择题 ‎1. C 2. D 3. C 4. A 5. C 6. D 7. A 8. A ‎ 9. B 10. D 11. A 12. B 三、解答题 ‎1. 解．（1）S圆环＝a2 ‎ ‎（2）弦AB或BC或AC ‎ ‎（3）圆环的面积均为·（）2. ‎ ‎（4）S圆环＝a2‎ ‎2. 解：⑴点P的坐标是（2，3）或（6，3） ‎ ‎⑵作AC⊥OP，C为垂足 ‎∵∠ACP＝∠OBP＝，∠1＝∠1‎ ‎∴△ACP∽△OBP ‎∴‎ 在中，‎ ‎，又AP＝12－4＝8， ∴‎ ‎∴AC＝≈1.94‎ ‎∵1.94<2‎ ‎∴OP与⊙A相交．‎ ‎3. 解：（1）在中，，‎ ‎．‎ ‎，．‎ ‎．‎ ‎，．‎ ‎（2）与⊙A 相切．‎ 在中，，，‎ ‎，．‎ 又，，‎ 与⊙A 相切．‎ ‎（3）因为，所以的变化范围为．‎ 当⊙A与⊙C 外切时，R＋r＝10，所以的变化范围为；‎ 当 ⊙A与⊙C 内切时，，所以的变化范围为．‎ ‎4. 证明：（1）等腰直角 ‎ ‎（2）问题一：△PEF是等腰直角三角形 ‎ 证明：连接PA、PB ‎ ‎∵AB是直径，∴∠AQB＝∠EQF＝90°‎ ‎∴EF是⊙O′的直径，∴∠EPF＝90° ‎ 在△APE和△BPF中：∵PA＝PB，∠PBF＝∠PAE ‎∠APE＝∠BPF＝90°＋∠EPB，∴△APE≌△BPF ‎∴PE＝PF，∴△PEF是等腰直角三角形 ‎ 问题二：参照问题一 ‎5. 解：设该两层卫生纸的厚度为xcm 则：11×11.4×x×300＝π（5.82－2.32）×11‎ x≈0.026‎ ‎ 答：该两层卫生纸的厚度约为‎0.026cm．‎ ‎6. （1）解：‎ d、a、r之间的关系 公共点的个数 D＞a＋r ‎0‎ d＝a＋r ‎1‎ a－r＜d＜a＋r ‎2‎ D＝a－r ‎1‎ D＜a－r ‎0‎ 所以，当r＜a时，⊙O与正方形的公共点的个数可能有0、1、2个； ‎ ‎（2）‎ d、a、r之间的关系 公共点的个数 d＞a＋r ‎0‎ d＝a＋r ‎1‎ a≤d＜a＋r ‎2‎ d＜a ‎4‎ 所以，当r＝a时，⊙O与正方形的公共点个数的可能有0、1、2、4个；‎ ‎（3）方法一：如图所示，连结OC．‎ 则OE＝OC＝r ，OF＝EF－OE＝‎2a－r． ‎ 在Rt△OCF中，由勾股定理得：OF2＋FC2＝OC2‎ 即（‎2a－r）2＋a2＝r2‎ ‎4a‎2－4ar＋r2＋a2＝r2‎ ‎5a‎2＝4ar ‎5a＝4r ‎∴r＝A．‎ 方法二：如图，连结BD、OE、BE、DE．‎ ‎∵四边形BCMN为正方形 ‎∴∠C＝∠M＝∠N＝90°‎ ‎∴BD为⊙O的直径，∠BED＝90°‎ ‎∴∠BEN＋∠DEM ＝90°‎ ‎∵∠BEN＋∠EBN＝90°‎ ‎∴∠DEM＝∠EBN ‎∴△BNE∽△EMD ‎ ‎∴‎ ‎∴DM＝a 由OE是梯形BDMN的中位线 得OE＝（BN＋MD）＝A．‎ ‎（4）①当a＜r＜时，⊙O与正方形的公共点的个数可能有0、1、2、4、6、7、8个；‎ ‎②当r＝a时，⊙O与正方形的公共点的个数可能有0、1、2、5、8个；‎ ‎③当时，⊙O与正方形的公共点的个数可能有0、1、2、3、4、6、8个；‎ ‎④当时，⊙O与正方形的公共点的个数可能有0、1、2、3、4个；‎ ‎⑤当时，⊙O与正方形的公共的点个数可能有0、1、2、3、4个．‎