人教版六年级数学上册第五单元 第6课时 圆与正方形组合的面积问题的应用（授课课件）

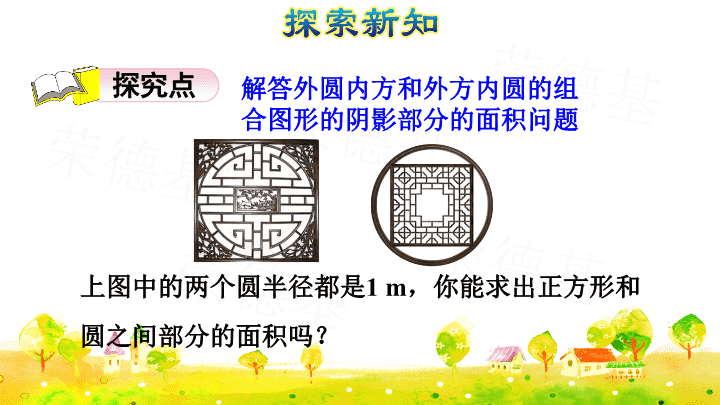
人教版六年级数学上册第五单元 第6课时 圆与正方形组合的面积问题的应用（授课课件）

荣德基 荣德基 荣德基 荣德基 荣德基 第6课时 圆与正方形组合的 面积问题的应用 RJ 六年级上册 5 圆 荣德基 荣德基 荣德基 荣德基 荣德基 中国建筑中经常能见到“外方内圆”和 “外圆内方”的设计。 外方内圆和外圆内方的图形是怎样组成的？ 它有什么特点？ 荣德基 荣德基 荣德基 荣德基 荣德基 探究点 解答外圆内方和外方内圆的组 合图形的阴影部分的面积问题 上图中的两个圆半径都是1 m，你能求出正方形和 圆之间部分的面积吗？ 荣德基 荣德基 荣德基 荣德基 荣德基 题目中都 告诉了我 们什么？ 上图中两个圆 的半径都是1 m， 怎样求正方形 和圆之间部分 的面积呢？ 左图求的是正 方形比圆多的 面积，右图求 的是…… 荣德基 荣德基 荣德基 荣德基 荣德基 从图（1）可以看出： 2×2＝4（m²） 4－3.14＝0.86（m²） 3.14×1²＝3.14（m²） 你能解决这个问题吗？ 图（1） 右图中正方形 的边长就是圆 的直径。 荣德基 荣德基 荣德基 荣德基 荣德基 3.14－2＝1.14（m²） 从图（2）可以看出： 下图中正方形的边长是多少呢？ 图（2） 可以把图中的正方形看成两个三 角形，它的底和高分别是……  21 2 1 2 = 2 m 2        荣德基 荣德基 荣德基 荣德基 荣德基 左图：(2r)²－3.14×r²＝0.86r² 答：左图中正方形与圆之间的面积是0.86 m²， 右图中圆与正方形之间的面积是1.14 m²。 那么我们解答得对不对呢？ 有什么方法验证吗？ 右图： 2 213.14 2 2 = 1.14 2 r r r r        － 当r＝1 m时，和前面的结果完全一致。 如果两个圆的半径都 是r，结果又是怎样的？ 荣德基 荣德基 荣德基 荣德基 荣德基 底a＝ 直径d 高 h＝ 半 径 r 圆的面积－正方形的面积正方形的面积－圆的面积 外方内圆 外圆内方 （2r）²－3.14×r²＝0.86r² 2 213.14 2 2 = 1.14 2 r r r r        － 荣德基 荣德基 荣德基 荣德基 荣德基 夯实基础 1. 右图是一面我国唐代外圆内方的铜镜。铜镜的 直径是24 cm。外面的圆与内部的正方形之间 的面积是多少？ 答：外面的圆与内部的正方形之间的面积约是164.16cm² 。 1.14×(24÷2)²＝164.16（cm²） （选题源于教材P70做一做） 荣德基 荣德基 荣德基 荣德基 荣德基 2．计算阴影部分面积。 4×4－3.14×(4÷2)2 ＝3.44(cm2) (1) (2) (5×2)2－3.14×52 ＝21.5(m2) 荣德基 荣德基 荣德基 荣德基 荣德基 3．解决问题 （1）在一块边长为20 cm的正方形铁片中，截取如图 所示的两个半圆，求剩余铁片的面积。 202－3.14×(20÷2)2＝86(cm2) 答：剩余铁片的面积是86平方厘米。 荣德基 荣德基 荣德基 荣德基 荣德基 (2)如下图，一枚铜钱的直径为22 mm，中间的正方 形的边长为6 mm。这枚铜钱的面积是多少？ 3.14×(22÷2)2－6×6＝343.94(mm2) 答：这枚铜钱的面积是343.94平方毫米。 荣德基 荣德基 荣德基 荣德基 荣德基 易错辨析 选一选 下面三个正方形的边长都是4 cm，阴影部分的面积 相比，(　　)。 A．第一个大　　　　 B．第二个大 C．第三个大 D．一样大 D 荣德基 荣德基 荣德基 荣德基 荣德基 辨析：第一个图形是挖去一个完整的圆，第二个 图形是挖去两个半圆，第三个图形是挖去 了四个四分之一圆，所以剩余的阴影面积 是一样的。 荣德基 荣德基 荣德基 荣德基 荣德基 这节课你有什么收获？ 荣德基 荣德基 荣德基 荣德基 荣德基 1.“外方内圆”图形中，圆的直径等于正方形的边长。 如果圆的半径为r，那么正方形和圆之间部分的面 积为0.86r2。 2.“外圆内方”图形中，这个正方形的对角线等于圆 的直径。如果圆的半径为r，那么圆和正方形之间 部分的面积为1.14r2。 荣德基 荣德基 荣德基 荣德基 荣德基 作 　 业 　请完成教材第72页练习十五第9题~第14题。 荣德基 荣德基 荣德基 荣德基 荣德基