- 2022-02-11 发布 |
- 37.5 KB |
- 16页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
六年级数学教案 《策略与方法二(数形结合)》
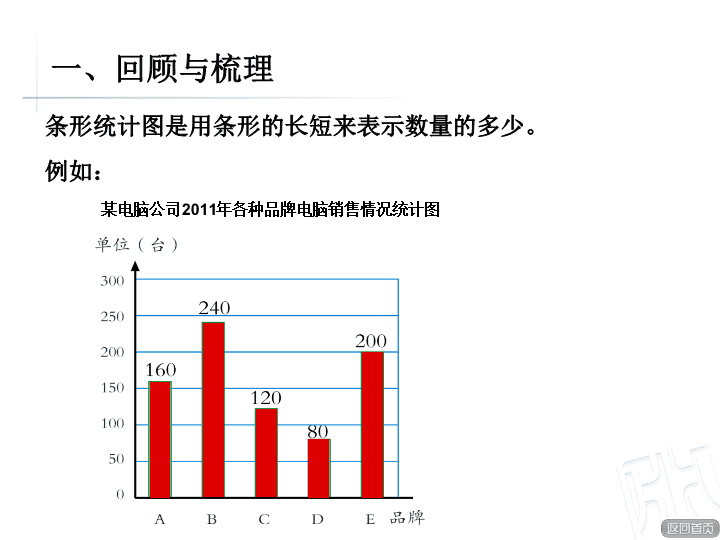
回顾与梳理 应用与反思 讨论与交流 总结与评价 策略与方法(二) — 数形结合 一、回顾与梳理 怎样把数与形结合起来解决问题呢? ● 统计图是借助图形描述数据的一种直观、有效的形式。 一、回顾与梳理 某电脑公司 2011 年各种品牌电脑销售情况统计图 条形统计图是用条形的长短来表示数量的多少。 例如: 折线统计图是用折线 的上升或下降来表示数量的增减变化情况 一、回顾与梳理 例如: 某电脑公司 2011 年各种品牌电脑销售情况统计图 扇形统计图是用扇面的大小来表示各部分占总数的百分之几。 一、回顾与梳理 例如: ● 借助画图的方法可以帮助我们理解计算方法。 × 1 2 3 5 1 2 3 5 = 3 10 一、回顾与梳理 例如: 2÷2=1 ( cm ) 每份长 1 厘米 ● 借助线段图可以帮助我们直观地理解数量关系。 一、回顾与梳理 去年收入: 160 万元 今年收入: 比去年增加 ?万元 1 4 李叔叔的有机蔬菜基地去年收入 160 万元,今年的收入比去年增加 ,今年收入多少万元? 1 4 例如: 1 4 160× ( 1+ ) 广场上 有一块长方形花坛,长 9 米。改建时,花坛的长增加了 3 米,这样花坛的面积就增加了 15 平方米。花坛原来的面积是多少平方米?(你能用数形结合的方法解答吗 ? ) 9 米 3 米 增加的 15 平方米 原来花坛的面积 ?平方米 试一试 先求增加的长方形的宽: 15 ÷ 3 = 5 (米) 再求原来长方形的面积: 9 × 5 = 45 (平方米) 答: 花坛原来的面积是 45 平方米。 ● 正比例图像也是用图形描述成正比例关系的两种量的直观形式。 0 1 2 3 4 5 6 时间(时) 80 160 240 320 400 480 路程(千米) 汽车行驶的时间和路程的变化情况,用图像描述更加形象。 二、讨论与交流 例如: o 北 ● 在平面内确定物体的位置时,也是把数与形结合起来思考。 0 1 2 3 4 5 1 2 3 4 5 A (3,2) B 30° B 在 O 点北偏东 30° 方向 100 米处。 100 米 二、讨论与交流 例如: 二、讨论与交流 结合刚才的梳理过程,说说“数形结合”的主要作用有哪些? 化难为易 化繁为简 化抽象为直观 三、应用与反思 1. 你能用直线上的点表示出下列各数吗? 3 , 1.5 , -1.5 , 0 , -0.5 0 1 2 3 4 5 6 -1 -2 1.5 -1.5 -0.5 三、应用与反思 比菊花少 25% 百合: 菊花: 30 盆 ?盆 多 15% 桃树: ?棵 120 棵 苹果树: 120× ( 1+15% ) = 138 ( 元 ) 2. 看图列式计算。 30÷ ( 1-25% ) = 40 (盆) 3. 一块菜地种植了 4 种蔬菜,分布情况如下图。若土豆的种植面积是 360 ㎡ ,黄瓜的面积比西红柿多多少平方米? 三、应用与反思 1 - 25% - 35% - 10% = 30% 360 ÷ 30% = 1200 (平方米) 1200× ( 35%-25% ) = 120 (平方米) 答:黄瓜的面积比西红柿多 120 平方米。 油菜 10% 土豆 黄瓜 35% 西红柿 25% 4. 灯塔南偏西 30 ° 方向 15 千米处是无名岛,你能在图中表示出它的位置吗? 0 北 南 西 东 15 千米 5 10 灯塔 30° ⊙ 无名岛 三、应用与反思 ⊙ 谢谢!查看更多