2012-2013学年山东省济南市芙蓉小学五年级（下）期中数学试卷（6）

2012-2013学年山东省济南市芙蓉小学五年级（下）期中数学试卷（6）

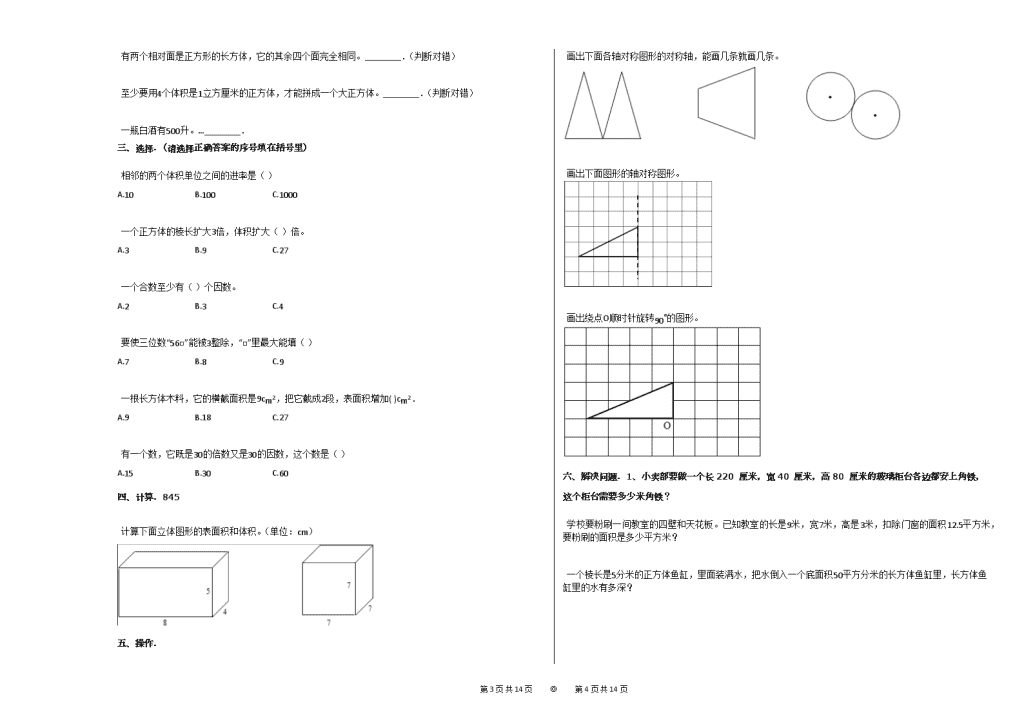
‎2012-2013学年山东省济南市芙蓉小学五年级（下）期中数学试卷（6）‎ 一、直接写出得数．‎ ‎ ‎ ‎1. 直接写出得数。 ‎ ‎1.53−0.5‎‎＝‎ ‎7.8+0.9‎‎＝‎ ‎7.5−2.5‎‎＝‎ ‎12÷0.4‎‎＝‎ ‎0.56+4.44‎‎＝‎ ‎2.9+3.7+2.1‎‎＝‎ ‎4×0.25‎‎＝‎ ‎1.25×5×8‎‎＝‎ ‎7.6×8+2.4×8‎‎＝‎ 二、填空．‎ ‎ ‎ ‎ 如图 ‎ ‎（1）指针从“‎1‎”绕点O顺时针旋转‎60‎‎∘‎后指向________‎ ‎ ‎ ‎（2）指针从“‎1‎”绕点O逆时针旋转‎90‎‎∘‎后指向________‎ ‎ ‎ ‎（3）指针从“‎7‎”绕点O逆时针旋转‎90‎‎∘‎后指向________‎ ‎ ‎ ‎（4）指针从‎5‎绕点O旋转到‎12‎点，顺时针要旋转________度，逆时针要旋转________度。‎ ‎ ‎ ‎ ‎3.05m＝ ‎305‎ cm ‎10.8‎m‎2‎＝ ‎1080‎ dm‎2‎ ‎6050cm‎3‎＝ ‎6.05‎ dm‎3‎ ‎2800mL＝ ‎2.8‎ L＝ ‎2.8‎ dm‎3‎． ‎ ‎ ‎ ‎ 在括号里填上适当的体积单位或容积单位。 ‎ ‎ ‎ ‎ 长方体和正方体都有________个面，________条棱，________个顶点。 ‎ ‎ ‎ ‎ ‎36‎和‎9‎，________是________的倍数，________是________的因数。 ‎ ‎ ‎ ‎ 按要求写出：‎12‎的所有因数：________，‎50‎以内‎12‎的倍数：________． ‎ ‎ ‎ ‎ 从‎0‎、‎5‎、‎6‎、‎7‎四个数中任意抽出‎3‎个，按要求组成‎4‎个不同的三位数：奇数________；‎3‎的倍数________； 偶数________；既是‎3‎的倍数又是‎5‎的倍数________． ‎ ‎ ‎ ‎ 最小的自然数与最小的质数和最小的合数的和是________． ‎ ‎ ‎ ‎ 两个质数的和是‎10‎，积是‎21‎，它们分别是________和________． ‎ ‎ ‎ ‎ 同时是‎2‎、‎3‎、‎5‎的倍数的最小两位数是________，最大两位数是________，最小三位数是________． ‎ ‎ ‎ ‎ 一个正方体的棱长扩大‎2‎倍，表面积就扩大________倍。 ‎ ‎ ‎ ‎ 一个长方体和一个正方体的棱长总和相等，已知长方体的长是‎6cm，宽是‎5cm，高是‎4cm，那么正方体的棱长是________的体积比较大。 ‎ 二、判断题 ‎ ‎ ‎ 平行四边形是轴对称图形。________．（判断对错） ‎ ‎ ‎ ‎ 一个自然数不是奇数就是偶数。________（判断对错） ‎ ‎ ‎ 第13页 共14页 ◎ 第14页 共14页 ‎ 有两个相对面是正方形的长方体，它的其余四个面完全相同。________．（判断对错） ‎ ‎ ‎ ‎ 至少要用‎4‎个体积是‎1‎立方厘米的正方体，才能拼成一个大正方体。________．（判断对错） ‎ ‎ ‎ ‎ 一瓶白酒有‎500‎升。…________． ‎ 三、选择．（请选择正确答案的序号填在括号里）‎ ‎ ‎ ‎ 相邻的两个体积单位之间的进率是（ ） ‎ A.‎10‎ B.‎100‎ C.‎‎1000‎ ‎ ‎ ‎ 一个正方体的棱长扩大‎3‎倍，体积扩大（ ）倍。 ‎ A.‎3‎ B.‎9‎ C.‎‎27‎ ‎ ‎ ‎ 一个合数至少有（ ）个因数。 ‎ A.‎2‎ B.‎3‎ C.‎‎4‎ ‎ ‎ ‎ 要使三位数“‎56‎□”能被‎3‎整除，“□”里最大能填（ ） ‎ A.‎7‎ B.‎8‎ C.‎‎9‎ ‎ ‎ ‎ 一根长方体木料，它的横截面积是‎9cm‎2‎，把它截成‎2‎段，表面积增加‎(‎ ‎)cm‎2‎． ‎ A.‎9‎ B.‎18‎ C.‎‎27‎ ‎ ‎ ‎ 有一个数，它既是‎30‎的倍数又是‎30‎的因数，这个数是（ ） ‎ A.‎15‎ B.‎30‎ C.‎‎60‎ 四、计算．845‎ ‎ ‎ ‎ 计算下面立体图形的表面积和体积。（单位：cm） ‎ 五、操作．‎ ‎ ‎ ‎ 画出下面各轴对称图形的对称轴，能画几条就画几条。 ‎ ‎ ‎ ‎ 画出下面图形的轴对称图形。 ‎ ‎ ‎ ‎ 画出绕点O顺时针旋转‎90‎‎∘‎的图形。 ‎ 六、解决问题．1、小卖部要做一个长220厘米，宽40厘米，高80厘米的玻璃柜台各边都安上角铁，这个柜台需要多少米角铁？‎ ‎ ‎ ‎ 学校要粉刷一间教室的四壁和天花板。已知教室的长是‎9‎米，宽‎7‎米，高是‎3‎米，扣除门窗的面积‎12.5‎平方米，要粉刷的面积是多少平方米？ ‎ ‎ ‎ ‎ 一个棱长是‎5‎分米的正方体鱼缸，里面装满水，把水倒入一个底面积‎50‎平方分米的长方体鱼缸里，长方体鱼缸里的水有多深？ ‎ 第13页 共14页 ◎ 第14页 共14页 参考答案与试题解析 ‎2012-2013学年山东省济南市芙蓉小学五年级（下）期中数学试卷（6）‎ 一、直接写出得数．‎ ‎1.‎ ‎【答案】‎ ‎1.03‎‎，‎8.7‎，‎5‎，‎30‎，‎5‎，‎8.7‎，‎1‎，‎50‎，‎‎80‎ ‎【考点】‎ 小数除法 小数四则混合运算 运算定律与简便运算 小数的加法和减法 小数乘法 ‎【解析】‎ ‎2.9+3.7+2.1‎运用加法交换律简算；‎1.25×5×8‎运用乘法交换律简算；‎7.6×8+2.4×8‎运用乘法分配律简算；其它题目按照运算法则直接求解。‎ ‎【解答】‎ ‎1.53−0.5‎‎＝‎1.03‎，‎7.8+0.9‎＝‎8.7‎，‎7.5−2.5‎＝‎5‎，‎12÷0.4‎＝‎30‎，‎0.56+4.44‎＝‎5‎， ‎2.9+3.7+2.1‎＝‎8.7‎，‎4×0.25‎＝‎1‎，‎1.25×5×8‎＝‎50‎，‎7.6×8+2.4×8‎＝‎80‎．‎ 二、填空．‎ ‎【答案】‎ ‎3‎ ‎10‎ ‎4‎ ‎210‎‎,‎‎150‎ ‎【考点】‎ 将简单图形平移或旋转一定的度数 ‎【解析】‎ 首根据题意，把李时间看单位“”，则陈红所用的时间是‎11‎‎9‎‎(1+‎2‎‎9‎=‎11‎‎9‎)‎，据此求出陈红李东的工作时间之比是少然根据工作量一定时，工作率作时成反比，求出陈红和的工作效率之是少可。‎ ‎【解答】‎ 解：因为陈红和李的工作时间是： 答：陈红和的工效率之比是‎9:1‎． ‎(1+‎2‎‎9‎)‎：‎1‎ 陈和李东的工作效率之比是‎9:1‎． ‎=119‎ 故答为：‎9:1‎．‎ ‎【答案】‎ ‎305‎‎、‎1080‎、‎6.05‎、‎2.8‎，‎‎2.8‎ ‎【考点】‎ 体积、容积进率及单位换算 面积单位间的进率及单位换算 ‎【解析】‎ ‎1‎米＝‎100‎厘米；‎1‎平方米＝‎100‎平方分米；‎1‎立方分米＝‎1000‎立方厘米，‎1‎立方厘米‎=‎‎1‎‎1000‎立方分米；‎1‎升＝‎1‎立方分米＝‎1000‎毫升，‎1‎毫升‎=‎‎1‎‎1000‎升；据此即可求解。‎ ‎【解答】‎ ‎3.05m‎＝‎305cm； ‎10.8‎m‎2‎＝‎1080dm‎2‎； ‎6050cm‎3‎＝‎6050×‎1‎‎1000‎dm‎3‎＝‎6.05dm‎3‎； ‎2800mL＝‎2.8L＝‎2.8dm‎3‎；‎ ‎【答案】‎ 解 ‎【考点】‎ 体积、容积及其单位 ‎【解析】‎ 根据容积单位、体积单位的意义，常用的容积单位有：升和毫升；常用的体积单位有：立方米、立方分米、立方厘米；然后根据实际生活情况进行解答即可。‎ ‎【解答】‎ 解 ‎【答案】‎ ‎6‎‎,‎12‎,‎‎8‎ ‎【考点】‎ 正方体的特征 ‎【解析】‎ 根据长方体和正方体的特征即可解决。‎ ‎【解答】‎ 根据长方体和正方体的特征可得；长方体和正方体都有‎6‎个面，‎12‎条棱，‎8‎个顶点，‎ ‎【答案】‎ ‎36‎‎,‎9‎,‎9‎,‎‎36‎ ‎【考点】‎ 因数和倍数的意义 ‎【解析】‎ 第13页 共14页 ◎ 第14页 共14页 根据因数和倍数的意义进行解答即可。‎ ‎【解答】‎ ‎36‎和‎9‎，‎36‎是‎9‎的倍数，‎9‎是‎36‎的因数；‎ ‎【答案】‎ ‎1‎‎、‎2‎、‎3‎、‎4‎、‎6‎、‎12‎,‎12‎、‎24‎、‎36‎、‎‎48‎ ‎【考点】‎ 找一个数的因数的方法 找一个数的倍数的方法 ‎【解析】‎ 根据找一个数因数的方法，列举出‎18‎的因数； 根据找一个数倍数的方法，列举出‎50‎以内的‎18‎的所有倍数；据此解答。‎ ‎【解答】‎ 解：‎12‎的因数有：‎1‎、‎2‎、‎3‎、‎4‎、‎6‎、‎12‎； ‎50‎以内的‎12‎的所有倍数：‎12‎、‎24‎、‎36‎、‎48‎． 故答案为：‎1‎、‎2‎、‎3‎、‎4‎、‎6‎、‎12‎；‎12‎、‎24‎、‎36‎、‎48‎．‎ ‎【答案】‎ ‎507‎‎、‎705‎、‎305‎、‎503‎；,‎507‎、‎705‎、‎750‎、‎570‎；,‎570‎、‎750‎、‎350‎、‎370‎；,‎570‎、‎750‎、‎705‎．‎ ‎【考点】‎ 奇数与偶数的初步认识 ‎2、3、5的倍数特征 ‎【解析】‎ 根据奇数、偶数的意义，‎3‎、‎5‎的倍数特征，在自然数中，是‎2‎的倍数的数叫做偶数，不是‎2‎的倍数的‎2‎数叫做奇数。‎3‎的倍数特征是：各位上的数的和是‎3‎的倍数，这个数一定是‎3‎的倍数，个位上是‎0‎或‎5‎的数是‎5‎的倍数。据此解答。‎ ‎【解答】‎ 从‎0‎、‎5‎、‎3‎、‎7‎四个数中任意抽出‎3‎个组成的三位数， 奇数有：‎507‎、‎705‎、‎305‎、‎503‎； ‎3‎的倍数有：‎507‎、‎705‎、‎750‎、‎570‎； 偶数有：‎570‎、‎750‎、‎350‎、‎370‎； 既是‎3‎的倍数又是‎5‎的倍数：‎570‎、‎750‎、‎705‎．‎ ‎【答案】‎ ‎6‎ ‎【考点】‎ 质数与合数问题 自然数的认识 ‎【解析】‎ 表示物体个数的数叫自然数，最小的自然数为‎0‎；自然数中，除了‎1‎和它本身之外没有别的因数的数为质数，除了‎1‎和它本身外还有别的因数的数为合数。由此可知，最小质数为‎2‎，最小的合数为‎4‎，据此即能求出它们的和是多少。‎ ‎【解答】‎ 最小的自然数是‎0‎，最小的质数是‎2‎，最小的合数的和是‎4‎，它们的和为： ‎0+2+4‎＝‎6‎．‎ ‎【答案】‎ ‎3‎‎,‎‎7‎ ‎【考点】‎ 质数与合数问题 ‎【解析】‎ 将‎21‎分解质因数为‎21‎＝‎3×7‎，又‎3+7‎＝‎10‎，所以这两个质数分别是‎3‎和（7）‎ ‎【解答】‎ ‎21‎‎＝‎3×7‎， ‎3+7‎＝（10） 即这两个质数分别是‎3‎和（7）‎ ‎【答案】‎ ‎30‎‎,‎90‎,‎‎120‎ ‎【考点】‎ 数的整除特征 ‎2、3、5的倍数特征 ‎【解析】‎ ‎（1）（2）根据‎2‎、‎3‎、‎5‎的倍数的倍数特征可知；同时是‎2‎、‎3‎、‎5‎的倍数的倍数，只要是个位是‎0‎，十位满足是‎3‎的倍数即可，十位满足是‎3‎的倍数的有；‎3‎、‎6‎、‎9‎，其中‎3‎是最小的，‎9‎是最大的，据此求出最大与最小； （3）同时是‎2‎、‎3‎、‎5‎的倍数的倍数的最小的三位数，只要个位是‎0‎，百位是最小的自然数‎1‎，十位满足和百位、个位上的数加起来是‎3‎的倍数即可，这样的数有：‎2‎、‎5‎、‎8‎，其中‎2‎是最小的，据此求出。‎ ‎【解答】‎ 同时是‎2‎、‎3‎、‎5‎的倍数的最小两位数是‎30‎，最大两位数是‎90‎，最小三位数是‎120‎；‎ ‎【答案】‎ ‎4‎ ‎【考点】‎ 长方体和正方体的表面积 积的变化规律 ‎【解析】‎ 根据正方体的表面积公式和积的变化规律，正方体的表面积公式：s＝‎6‎a‎2‎，积扩大的倍数等于因数扩大倍数的乘积，正方体的棱长扩大‎2‎倍，表面积就扩大‎4‎倍。‎ ‎【解答】‎ 答：一个正方体的棱长扩大‎2‎倍，表面积就扩大‎4‎倍。 故答案为：‎4‎．‎ ‎【答案】‎ ‎5cm‎，表面积是‎150cm‎2‎，与长方体比较，正方体 ‎【考点】‎ 长方体和正方体的体积 长方体和正方体的表面积 ‎【解析】‎ 由“一个长方体和一个正方体的棱长总和相等，已知长方体的长是‎6cm，宽是‎5cm，高是‎4cm”可知，正方体的棱长和＝长方体的棱长和＝‎[(6+5+4)×4]‎厘米，进而可以求出正方体的棱长；从而可以分别求出其表面积和体积；再与长方体的体积相比，即可知道谁大谁小。‎ ‎【解答】‎ 正方体的棱长＝‎(6+5+4)×4÷12‎， ＝‎15×4÷12‎， ＝‎60÷12‎， ＝‎5‎（厘米）； 正方体的表面积＝‎5×5×6‎＝‎150‎（平方厘米）； 正方体的体积＝‎5×5×5‎＝‎125‎（立方厘米）； ‎ 第13页 共14页 ◎ 第14页 共14页 长方体的体积＝‎6×5×4‎＝‎120‎（立方厘米）； 所以正方体的体积大于长方体的体积。‎ 二、判断题 ‎【答案】‎ 错误 ‎【考点】‎ 轴对称图形的辨识 ‎【解析】‎ 依据轴对称图形的定义即可作答。‎ ‎【解答】‎ 因为平行四边形无论沿哪一条直线对折，对折后的两部分都不能完全重合，所以平行四边形不是轴对称图形。 答：平行四边形是轴对称图形，这种说法是错误的。 故答案为：错误。‎ ‎【答案】‎ ‎√‎ ‎【考点】‎ 奇数与偶数的初步认识 ‎【解析】‎ 奇数与偶数是按能否被‎2‎整除划分的，两部分合在一起，构成了自然数，由此判定即可。‎ ‎【解答】‎ 自然数按能否被‎2‎整除分为奇数和偶数，所以所有的自然数不是偶数就是奇数是正确的。‎ ‎【答案】‎ 正确 ‎【考点】‎ 长方体的特征 ‎【解析】‎ 假设是上、下两个面都是正方形的长方体，即长方体的长和宽相等，其它四个面的面积都等于正方形的边长‎×‎高，因为正方形的边长都相等，长方体的高不变，所以它的其余四个面完全相同，面积相等。‎ ‎【解答】‎ 解：由分析知：有两个相对面是正方形的长方体，它的其余四个面完全相同，面积相等； 故答案为：正确。‎ ‎【答案】‎ 错误 ‎【考点】‎ 长方体和正方体的体积 ‎【解析】‎ 体积是‎1‎立方厘米的正方体的棱长是‎1‎厘米，用它拼成一个大正方体，这个大正方体的棱长至少是‎2‎厘米，它的体积就是‎2‎‎3‎‎=8‎立方厘米，再看‎8‎立方厘米里面有几个‎1‎立方厘米，就是至少用的‎1‎立方厘米的正方体个数。‎ ‎【解答】‎ 解：根据题意这个大正方体的棱长至少是‎2‎厘米， 体积是：‎2‎‎3‎‎=8‎立方厘米， ‎1‎立方厘米的正方体个数：‎8÷1=8‎（个）； 答：至少要用‎8‎个体积是‎1‎立方厘米的正方体，才能拼成一个大正方体。 故判断为：错误。‎ ‎【答案】‎ 错误 ‎【考点】‎ 根据情景选择合适的计量单位 ‎【解析】‎ 根据题意知，酒的多少要用容积单位，数量为‎500‎毫升，由此可以进行判断。‎ ‎【解答】‎ 由题意知，酒的多少要用容积单位， 根据生活实际知，数量应为‎500‎毫升，“升”这个单位太大了， 所以上面的说法是错误的，‎ 三、选择．（请选择正确答案的序号填在括号里）‎ ‎【答案】‎ C ‎【考点】‎ 体积、容积及其单位 ‎【解析】‎ 根据常用的体积单位，立方米、立方分米、立方厘米；以及相邻单位之间的进率解答即可。‎ ‎【解答】‎ ‎1‎立方米＝‎1000‎立方分米； ‎1‎立方分米＝‎1000‎立方厘米；‎ ‎【答案】‎ C ‎【考点】‎ 长方体和正方体的体积 ‎【解析】‎ 正方体的体积等于棱长的立方，它的棱长扩大几倍，则它的体积扩大棱长扩大倍数的立方倍，据此规律可得。‎ ‎【解答】‎ 正方体的棱长扩大‎3‎倍，它的体积则扩大‎3‎‎3‎＝‎27‎倍。‎ ‎【答案】‎ B ‎【考点】‎ 质数与合数问题 ‎【解析】‎ 自然数中，除了‎1‎和它本身外还有别的因数的数为合数。由此可知，一个合数除了‎1‎和它本身外，至少还要有一个因数即至少有‎3‎个因数，如‎4‎，共有‎1‎，‎2‎，‎4‎三个因数。‎ ‎【解答】‎ 根据合数的意义可知， 一个合数除了‎1‎和它本身外，至少还要有一个因数，即至少有‎3‎个因数。‎ ‎【答案】‎ A ‎【考点】‎ 找一个数的倍数的方法 ‎【解析】‎ 根据能被‎3‎整除的数的特征：即该数各个数位上数的和能被‎3‎整除；进行解答即可。‎ ‎【解答】‎ 要使三位数“‎56‎□”能被‎3‎整除，因为‎5+6‎＝‎11‎，‎11+1‎＝‎12‎，‎11+4‎＝‎15‎，‎11+7‎＝‎18‎； ‎12‎、‎15‎和‎18‎都能被‎3‎整除，所以“□”里可以填‎1‎，‎4‎，‎7‎；最大为‎7‎；‎ 第13页 共14页 ◎ 第14页 共14页 ‎【答案】‎ B ‎【考点】‎ 长方体和正方体的体积 ‎【解析】‎ 根据题意，把它截成‎2‎段就会露出两个横截面，表面积也就是增加了‎2‎个横截面的面积，列式解答即可得到答案。‎ ‎【解答】‎ ‎9×2‎‎＝‎18‎（平方厘米），‎ ‎【答案】‎ B ‎【考点】‎ 找一个数的因数的方法 ‎【解析】‎ 由题意知：‎30‎的最小倍数是‎30×1‎＝‎30‎，最大约数是‎30‎，因为最大约数和最小倍数相等，故这个数为‎30‎．‎ ‎【解答】‎ 有一个数，它既是‎30‎的倍数又是‎30‎的因数，这个数就是‎30‎本身；‎ 四、计算．845‎ ‎【答案】‎ 长方体的表面积是‎184‎平方厘米，体积是‎160‎立方厘米。 （2）‎7×7×6‎＝‎294‎（平方厘米）（2）‎7×7×7‎＝‎343‎（立方厘米）（3）答：正方体的表面积是‎294‎平方厘米，体积是‎343‎立方厘米 ‎【考点】‎ 长方体和正方体的体积 长方体和正方体的表面积 ‎【解析】‎ ‎（1）由图可知，长方体的长是‎8‎厘米，宽是‎4‎厘米，高是‎5‎厘米，根据长方体的表面积公式：s＝‎(ab+ah+bh)×2‎，体积公式：v＝abh， （2）已知正方体的棱长是‎7‎厘米，根据正方体的表面积公式：s＝‎6‎a‎2‎，体积公式：v＝a‎3‎，由此列式解答；‎ ‎【解答】‎ ‎8×4×5‎‎＝‎160‎（立方厘米）（1）答：长方体的表面积是‎184‎平方厘米，体积是‎160‎立方厘米。 （2）‎7×7×6‎＝‎294‎（平方厘米）（2）‎7×7×7‎＝‎343‎（立方厘米）（3）答：正方体的表面积是‎294‎平方厘米，体积是‎343‎立方厘米。‎ 五、操作．‎ ‎【答案】‎ 解：如图所示，即为所要画的图形的对称轴； ．‎ ‎【考点】‎ 确定轴对称图形的对称轴条数及位置 ‎【解析】‎ 依据轴对称图形的概念及对称轴的条数即可作答。‎ ‎【解答】‎ 解：如图所示，即为所要画的图形的对称轴； ．‎ ‎【答案】‎ 画出下面图形的轴对称图形： ‎ ‎【考点】‎ 作轴对称图形 ‎【解析】‎ 根据轴对称图形的特征，对称点到对称轴的距离相等，对称点的连线垂直于对称轴，在对称轴的右边画出左图的关键对称点，连结即可。‎ ‎【解答】‎ 画出下面图形的轴对称图形： ‎ ‎【答案】‎ 解：画出绕点O顺时针旋转‎90‎‎∘‎的图形： ‎ 第13页 共14页 ◎ 第14页 共14页 ‎【考点】‎ 作旋转一定角度后的图形 ‎【解析】‎ 根据旋转的特征，三角形绕点O顺时旋转‎90‎‎∘‎后，点O的位置不动，其余各部分均绕此点按相同方向旋转相同的度数，即可画出旋转后的图形。‎ ‎【解答】‎ 解：画出绕点O顺时针旋转‎90‎‎∘‎的图形： ‎ 六、解决问题．1、小卖部要做一个长220厘米，宽40厘米，高80厘米的玻璃柜台各边都安上角铁，这个柜台需要多少米角铁？‎ ‎【答案】‎ 解：‎9×7+9×3×2+7×3×2−12.5‎ ‎=63+54+42−12.5‎， ‎=159−12.5‎， ‎=146.5‎（平方米）； 答：要粉刷的面积是‎146.5‎平方米。‎ ‎【考点】‎ 长方体、正方体表面积与体积计算的应用 ‎【解析】‎ 首先搞清这道题是求长方体的表面积，其次这个长方体的表面由五个长方形组成，缺少下面，最后计算这五个面的面积减去门窗的面积，由此解决问题。‎ ‎【解答】‎ 解：‎9×7+9×3×2+7×3×2−12.5‎ ‎=63+54+42−12.5‎， ‎=159−12.5‎， ‎=146.5‎（平方米）； 答：要粉刷的面积是‎146.5‎平方米。‎ ‎【答案】‎ ‎5×5×5÷50‎‎ ＝‎125÷50‎， ＝‎2.5‎（分米）； 答：长方体鱼缸里的水有‎2.5‎分米深 ‎【考点】‎ 长方体和正方体的体积 ‎【解析】‎ 根据题意可知，把正方体鱼缸里面装满水，倒入长方体鱼缸里，水的体积不变，根据正方体的体积公式v＝a‎3‎，求出水的体积，再除以长方体的底面积就求出长方体鱼缸里的水有多深；由此列式解答。‎ ‎【解答】‎ ‎5×5×5÷50‎‎ ＝‎125÷50‎， ＝‎2.5‎（分米）； 答：长方体鱼缸里的水有‎2.5‎分米深 第13页 共14页 ◎ 第14页 共14页