五年级上册数学课件 数学好玩《图形中的规律》 北师大版 (共53张PPT)

五年级上册数学课件 数学好玩《图形中的规律》 北师大版 (共53张PPT)

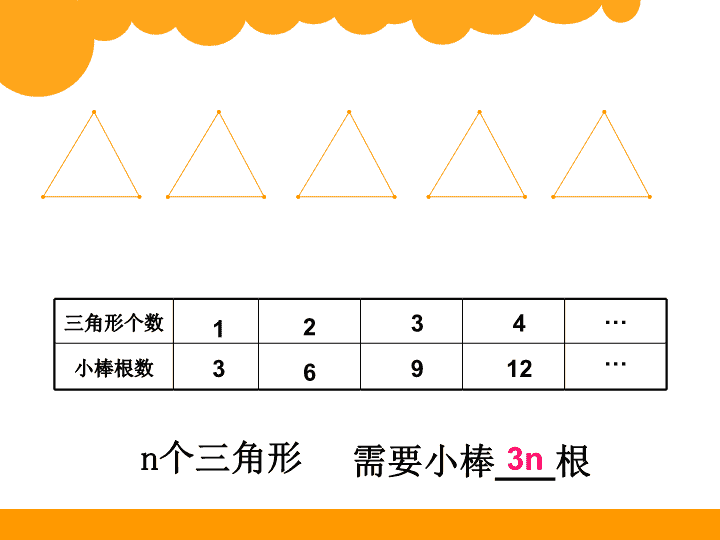
５、７、１、６、１４、（）、（） ２、４、８、（ ）、（ ）、６４ 、 、 16 32 北师大版 五年级上册 数学好玩 摆三角形 点阵中的规律 三角形个数 小棒根数 1 3 2 6 3 9 4 12 … … n个三角形 需要小棒___根3n 求n个单独的三角形的小棒数（边数） 我们可以用这样公式来概括这种规律： 3代表组成一个单 独三角形所需的 小棒数（边数） n代表图形（三角 形）的个数 …… 三角形个数 摆成的图形 小棒的根数 1 2 3 4 … 10 3 5 7 9 … 每多摆1个三角形就增加2根小棒。 =3+2 =3+2+2 =3+2+2+2 21 　摆成的图形 三角形的个数 小棒根数 1 2 3 4 3 3+2 3+2+2 3+2+2+2 …… 3+2x(n-1) 3+2x2 3+2x3 3+2x1 ………… n 3 5 7 9 3 + 2 ×（10-1） = 21（根） …… （10个） 3+2+2+2+2+2+2+2+2+2=21（根） 3 + 2 ×（n-1） 3+2(n-1) 　摆成的图形 三角形的个数 小棒根数 1 2 3 4 1+2 1+2+2 1+2+2+2 1+2+2+2+2 …… 1+2x2 1+2x3 1+2x4 n 1+2xn 1+2x1 ………… 3 5 7 9 …… （10个） 1 + 2 ×10 = 21（根） 1 + 2 ×n 1+2n或2n+1 1+2+2+2+2+2+2+2+2+2+2 = 21（根） 摆成的图形 三角形 的个数 小棒根数 1 2 3 4 3 3x2 3x3 3x4 3Xn-(n-1) ……………… -1 -2 -3 n 3 5 7 9 3×10 – (10-1) = 21（根） …… （10个） 3×n – (n-1) 3n-(n-1) 方法一： 写一写 方法二： 方法三： 3+2(n-1) 1+2n或2n+1 3n-(n-1) 1+2n或2n+1 摆100个三角形需要多少根小棒呢？ 摆n个三角形需要多少根小棒呢？ 用31根小棒可以摆几个三角形？ 摆正方形会有 什么规律呢？ 正方形个数 摆成的图形 小棒的根数 1 2 3 4 … 10 4 7 10 13 … 每多摆1个正方形就增加3根小棒。 4 + 3×19 摆 20个正方形需要多少根小棒？ 1 + 3×20 4×20 －19 …… 4+3(n-1) 4n-(n-1) 1+3n或3n+1 如果边数继续增加，五边形象这 样摆下去，你们还能说出这里的 规律么？六边形呢？ 1+4n五边形 六边形 1+5n 七边形 6n+1 八边形 7n+1 古希腊数学家 毕达哥拉斯 阿拉伯数字的发明，使我们记录和计算更加方便， 然而在表现一些数的特征方面，点阵更加直观。2300多 年前，古希腊数学家毕达哥拉斯就非常善于寻找点阵中 的规律，用点阵来研究数。 1 4 9 16 这些点阵图与 对应的数有什 么关系？和序 号呢？ 点阵 数 序号 321 4 5 25 25 能用数学算式表示25吗？ 序号 点阵中的规律 数 形（点阵） ① ② ④ ③ ⑤ 1 4 9 16 25 数形结合 横竖看 1×1= 1 2×2= 4 3×3= 9 4×4= 16 5×5= 25 斜着看 1 1+2+1 1+2+3+2+1 1+2+3+4+3+2+1 1+2+3+4+5+4+3+2+1 拐弯看 1+3=4 1+3+5=9 1+3+5+7=16 1+3+5+7+9=25 1 思考：这些算式与序号有什么关系？ 交流你的发现吧！ 　　　斜着观察发现，划分的9个图形， 随着图形的变化，图中的点数也发生变 化。左上图形点的个数是以第一个图形 的１点开始，从第二个图形往后依次增 加1点，第五个图形为5点，从第五个图 形向右下又依次减少一个点，到一点， 即1+2+3+4+5+4+3+2+1=5×5=25。 利用你的发现，计算一下： 1＋2＋3＋……＋99＋100＋99＋……＋3＋2＋1＝？ 100×100= 10000 交流你的发现吧！ 　　　拐弯观察发现，划分的五个图形均是 正方形（第一个图形除外），前后图形 点的个数是以第一个图形的１点开始， 第二个图形比第一个图形增加３点，第 三个图形比第二个图形增加５点，第四 个图形比第三个图形增加７点，第五个 图形比第四个图形增加９点，即１+３+ ５+７+9＝２５. 数缺形来少直观， 形缺数来难入微， 数形结合百般好， 隔离分家万事休。 中国现代著名数学家 华 罗 庚 试 一 试 观察下列点阵，并在括号中填上适当的 算式。 （1×2） （ ） （ ） （ ） 试着画出第5个点阵图。 2×3 3×4 4×5 ﹙5×6﹚ 观察点阵的规律，画出下一个图形。 试 一 试 1 =1 1+2 =3 1+2+ = = 你有什么发现？试 一 试 3 6 1+2+3+4 10 练一练 按下面的方法划分点阵中的点，并填写 算式。 1=1 4=1+2+1 9= 16=1+2+3+2+1 1+2+3+4+3+2+1 1+2+3 2+3+4 3+4+5 4+ + 第7个点阵有 ＿ 个点 观察图中,找一找有什么规律。 24 5 6 练一练 观察下图中已有的几个图形，按规律画出 下一个图形。 试 一 试 如图：正五边形点阵，它的中心是一个点，算做第 一层，第二层每边有两个点，第三层每边有三个点。 这个五边形点阵第12层有多少个点？ 如图所示,在正六边形周围画出6个同样的正六边形(阴 影部分),围成第1圈;在第1圈外面再画出12个同样的正 六边形,围成第2圈;……。按这个方法继续画下去,当 画完第6圈时,图中共有______个这样的正六边形。 21 1 21 3 2  23 6 3  26 10 4  25 如图:每个正方形点阵均被一直线分成两个三角形 点阵，根据图中提供的信息，用等式表示第５个正 方形点阵中的规律是 　　　　　　。 …… …… 10 ＋ 1５ ＝ 有一张蓝白相间的方格纸,用记号(3,2)表示从左往右数 第3列,从上往下数第2行的这一格(如图),那么(19,81)这 一格是______色。 3,2 • 1＋2＋3＋4＋5＋6＋7＋6＋5＋4＋3＋2＋1＝（　　　　　） • 1＋3＋5＋7＋9＋11＋13＝（　　　　） 7 × 7 7 × 7 根据左图①的变化，推断出右图② 右边问号处应选几号图？ ① ② 根据左图①的变化，推断出右图②右边 问号处应选几号图？ ① ② 根据前面三幅图的规律，在第四幅图中画出阴影部分。 根据前面三幅图的规律，在第四幅图中画出阴影部分。 点击出迷宫 如图，照这样摆下去，若摆到第1０层，一共需　　　　个正方体,　 其中 有 个, 有 个，若摆80层,一共需 　个正 方体,其中 有 个, 有 个。 100 55 45 1×1 2×2 3×3 4×4 …… n×n 一层 二层 三层 四层 n层 6400 3240 3160 1 2 4 3 1 3 15 7 1 4 χ 13 1 2 4 3 1 3 15 7 1 4 1340 观察鱼的排列规律,在“？”处画上鱼图。 ？ ？ 请从下面六个图中，选一个合适的填在“ ？ ”处。 笑笑接着摆下去，一共用了37根小棒，你知道她 摆了多少个三角形吗？ 37－3＝34 34÷2＝17 17＋1＝18 37－1＝36 36÷2＝18 观察每个点阵中点的个数，你发现了什么？ 1×1 1 2 3 2×2 3×3 4×4 5×5 1＋3 1＋3＋5 1＋3＋5＋71 1＋2＋1 1＋2＋3＋2＋1 1＋2＋3＋4＋3＋2＋11