- 2021-12-10 发布 |
- 37.5 KB |
- 23页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
四年级数学下册课件-5三角形的内角和-人教版 (10)
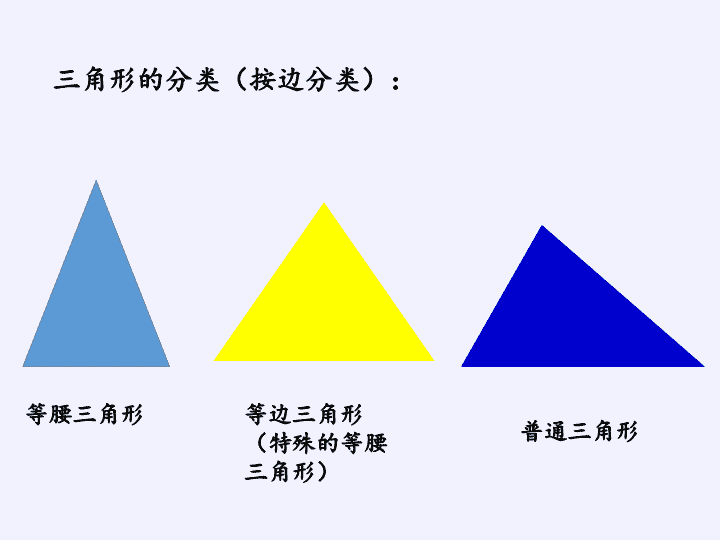
三角形的分类(按边分类) : 等腰三角形 等边三角形 (特殊的等腰 三角形) 普通三角形 教学内容:三角形的内角和。 教学目标:1、理解三角形内角和的定义; 2、熟练掌握并会运用三角形的内角和。 教学重点:探索发现三角形内角和等于180°并能应用 。 教学难点:三角形内角和是180°的探索和验证。 教学背景:学生在前面已经学过了三角形的特性和三角 形的种类,对三角形的已经基本了解。 教学用具:课件、不同的三角形卡片、量角器 形状似座山,稳定性能坚。 三竿首尾连,学问不简单。 (打一图形名称) 三角形 自主探究: 1:什么是三角形的内角? 2:三角形有几个内角? 3:什么是三角形的内角和? 1 2 3 ∠1+∠2+∠3 学习目标: 1、理解三角形内角和的定义; 2、熟练掌握并会运用三角形的 内角和。 我不服气,我 的内角和可不 一定比你们小 。 我的个头最大,所 以我的三个内角的 和一定是最大的。 我还有一个钝角呢,因此 我的三个内角的和肯定比 你大。 钝角三角形 260 1160 1160+260+380=1800 380 量 锐角三角形 量 480 720 600 600+480+720 =1800 活动小提示: 1、小组集体合作,充分利用手中 的学具进行验证; 2、比一比哪一组的方法多而且又 富有新意。 绿色圃中小学教育网 http://www.lspjy.com 3 平角:1800 平角:1800 平角:1800 1 1 2 2 3 1 2 1 2 3 3 1 2 312 3 180度 180度 180度 180度180度 数学文化 帕斯卡,法国数学家, 物理学家,近代概率论 的奠基者。早在300多 年前这位法国的科学家 就已经发现了任何三角 形的内角和是180度, 而他当时才12 岁。 (1)小丽量得一个三角形的三个内角分别是 35°、65°、90°。 ( ) (2) 钝角三角形中的两个锐角和一定小于90°。 ( ) (⑶)用一个放大10倍的放大镜看一个三角形, 这个三角形的内角和是1800°。 ( ) √ X X (1)、三角形∠1=140°,∠3=25° ,求∠2的度数。 仿例练习 180°-140°-25°=15° 180°-(140°+25°)=15° 答: ∠2的度数是15°。 140°25° (2) 爸爸给小红买了一个等腰三角形的风筝 。它的一个底角是70°,它的顶角是多少度? 180°-70°-70°= 40° 答:它的顶角是40° 仿例练习 180°-70°× 2 = 40° (1)、一个直角三角形的一个锐 角是35度,另一个锐角是多少度? 变例练习 35° ? 180°-90°-35°=55° 90°-35°=55° 答:另一个锐角的度数是55°。 (1)、一个等腰三角形的底角是45 度,它的顶角是多少度?这是一个什 么三角形? 讨论下列问题: (2)、一个等腰三角形的底角是 60°,它的顶角是多少度?这是一个 什么三角形?查看更多