- 2021-12-10 发布 |
- 37.5 KB |
- 21页

申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
5年级数学教案《回顾整理三》
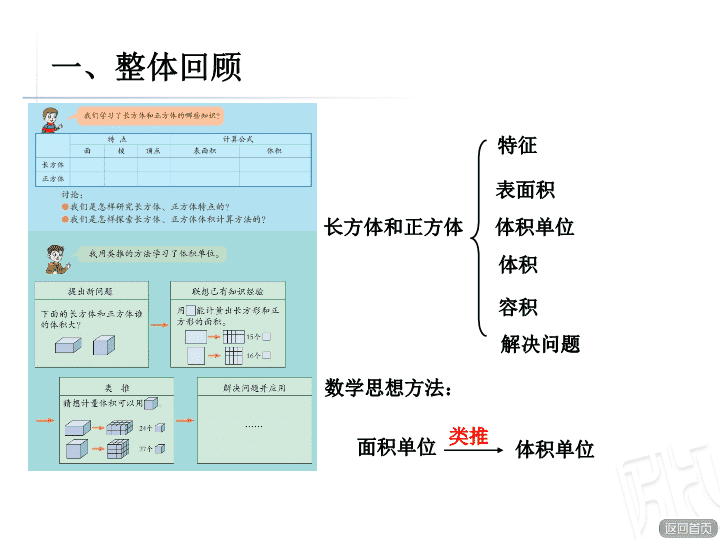
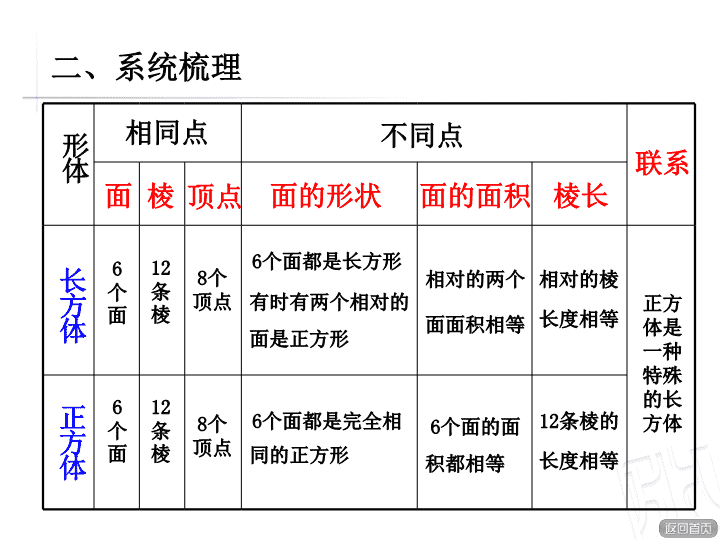
长方体和正方体回顾整理 评价反思 综合应用 系统梳理 整体回顾 小学五年级数学 一、整体回顾 长方体和正方体 特征 表面积 体积 容积 解决问题 体积单位 面积单位 类推 体积单位 数学思想方法: 形体 长方体 正方体 相同点 不同点 联系 面 顶点 面的形状 面的面积 棱长 棱 6 个 面 6 个 面 12 条 棱 12 条 棱 8 个 顶点 8 个 顶点 6 个面都是长方形 有时有两个相对的 面是正方形 6 个面都是完全相 同的正方形 相对的两个 面面积相等 6 个面的面 积都相等 相对的棱 长度相等 12 条棱的 长度相等 二、系统梳理 正方 体是 一种 特殊 的长 方体 二、系统梳理 概念 计算 公式 常用 单位 表面积 体积 容积 长方体或者正方体 6 个面的 总面积,叫做它的表面积。 物体所占空间的大 小叫做物体的体积。 容器所能容纳物体 的体积,通常叫做 它们的容积。 长方体: S=(ab+ah+bh)×2 正方体: S=6a 2 长方体: V=abh 正方体: V=a 3 V=Sh m 2 d m 2 cm 2 m 3 d m 3 cm 3 L mL 1m 2 =100dm 2 1dm 2 =100cm 2 1m 3 =1000dm 3 1dm 3 =1000cm 3 1L=1000mL 二、系统梳理 体积单位及体积单位的探索: 提出问题 联想已有知识经验 类推得出结论 二、系统梳理 类推得出结论 二、系统梳理 解决问题 解释应用 二、系统梳理 现实问题 数学问题 联想已有 知识经验 长方体、正方体体积计算方法的探索 : 二、系统梳理 寻找方法 算一算 二、系统梳理 归纳结论 二、系统整理 解决问题 解释应用 产生新问题 二、系统梳理 方法整理: 现实问题 怎样求饮料箱的体积? 数学问题 联想已有知识经验 归纳结论 解决问题、解释应用 产生新问题 怎样求长方体的体积? 面积的大小等于含有面积单位数的多少,体积的大小是否等于是含有体积单位数的多少。 猜想、验证、总结体积公式: v=abh 运用公式求出长方体的体积,解决求饮料箱体积的问题。 是不是所有立方体的体积都等于底面积乘高。 返回 寻找方法 切一切、摆一摆、数一数、算一算。 二、系统梳理 解决问题: 1. 一个长方体,长 5 厘米, 宽 4 厘米,高 3 厘米,这个 长方体的体积是多少? 5 ×4 × 3 = 60 (立方厘米) 2. 一个正方体,棱长是 4 厘米, 这个正方体的体积是多少? 4 ×4 × 4 = 64 (立方厘米) 二、系统梳理 解决问题: 3. 一个长方体鱼缸,底面积 是 50 平方分米,高 8 分米,这 个鱼缸的容积是多少升? 50×8 = 400 (立方分米) 4. 用 24 厘米的铁丝围成一个 正方体框架,正好用完,这个 正方体的体积是多少? 思考:求正方体的体积,需要 知道正方体的棱长, 24 厘米的 铁丝围成框架,就是 12 条棱的 长度是 24 厘米,正方体的棱长 都相等,所以这个正方体的一 条棱长是 2 厘米。 400 立方分米 = 400 升 24 ÷ 12 = 2 (厘米) 2×2×2 = 8 (立方厘米) 返回 二、系统梳理 解决问题 : 5. 把一个棱长为 10cm 的正方体木块切成两个完全相同的长方 体,切完后的表面积和体积有什么变化?分别是多少? 思考: 切割之后,形状发生了变化,增加了两个面,而占空间的大小并没有变化,所以,切割后的表面积比原来的正方体多了两个 面的面积,而体积与原来相同。 表面积: 正方体表面积: 10×10×6=600 ( cm 2 ) 增加的面积: 10×10×2=200 ( cm 2 ) 现在的表面积: 600+200= 800 ( cm 2 ) 体积: 10×10×10= 1000 ( cm 3 ) 三、综合应用 1. 我会填。 ( 1 ) 4900mL=( )L=( )dm 3 ( 2 )一盒酸奶的容积是 200 ( )(填上适当的单位) ( 4 )一个长方体鱼塘长 8 米,宽 4.5 米,深 2 米,这个鱼塘的容积 大约是( )立方米。 ( 3 )一个长方体的长是 2 分米,宽是 8 分米,高时 5 分米,它的棱长 总和是( )分米。 ( 5 ) 0.05 平方米 = ( )平方分米 = ( )平方厘米 4.9 4.9 毫升 60 72 5 500 三、综合应用 2. 游泳池长 50 米,宽 20 米,深 20 分米。 ( 1 )这个游泳池的占地面积是多少? 50 × 20 = 1000 (平方米) 答:这个游泳池的占地面积是 1000 平方米。 三、综合应用 ( 2 )需要挖出多少立方米的土? 50 × 20 × 2 = 2000 (立方米) 答:需要挖出 2000 立方米的土。 20 分米 =2 米 2. 游泳池长 50 米,宽 20 米,深 20 分米。 三、综合应用 ( 3 )如果给这个游泳池的池底和四周贴上瓷砖,每平方 米需要 10 块瓷砖,那么至少需要多少块这样的瓷砖? 50×20+50×2×2+20×2×2= 1280 (平方米) 答:至少需要 12800 块这样的瓷砖。 1280×10= 12800 (块) 2. 游泳池长 50 米,宽 20 米,深 20 分米。 三、综合应用 ( 4 )如果在游泳池中放入 1.8 米深的水,那么一共 需要多少立方米? 50 × 20 ×1.8 = 1800 (立方米) 答:一共需要 1800 立方米水。 2. 游泳池长 50 米,宽 20 米,深 20 分米。 总 结 这节课你学会了什么?你有什么要提醒同学们注意的? 总结评价查看更多