2019九年级数学上册 第24章 解直角三角形 24测量

2019九年级数学上册 第24章 解直角三角形 24测量

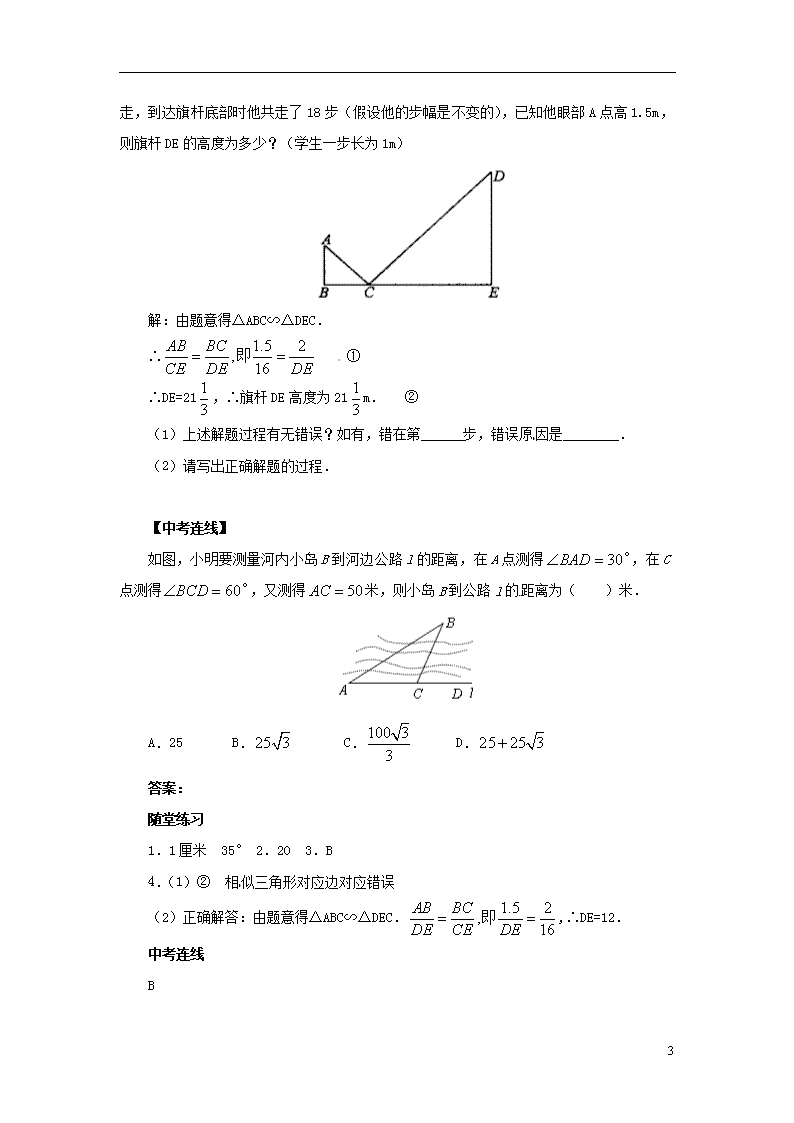
‎24.1 测量 ‎【学习目标】‎ 1、 了解测量的方法；‎ 2、 运用测量的方法解决实际问题.‎ ‎【学习重难点】‎ 掌握测量的方法.‎ ‎【学习过程】‎ 一、课前准备 当你走进学校，仰头望着操场旗杆上高高飘扬的五星红旗时，你也许想知道操场旗杆有多高？我们知道可以利用相似三角形的对应边，首先请同学量出太阳下自己的影子长度，旗杆的影子长度，再根据自己的身高，计算出旗杆的高度。如果在阴天，你一个人能测量出旗杆的高度吗？‎ 二、学习新知 自主学习：‎ 试一试.‎ 如图所示，站在离旗杆BE底部10米处的D点，目测旗杆的顶部，视线AB与水平线的夹角∠BAC=34°，并已知目高AD为1米。现在请你按1：500的比例得△ABC画在纸上，并记为△A1B1C1,用刻度尺量出纸上B1C1的长度，便可以算出旗杆的实际高度。你知道计算的方法吗？‎ 设计一种方案，测量学校科技楼的高度。请写出测量的过程，并简要说明这样做的理由。‎ 分析：测量大楼的高度的方法很多，现采用一种方法，利用人的身高和标杆，依据相似三角形三角对应成比例和平行线的性质，可测出大楼的高度。‎ 解答：测量过程如下：‎ ‎1、在地面上立一个标杆，使人眼、杆顶、楼顶在一条直线上。‎ ‎2、测出CF、CH的距离 ‎3、算出KE的长度。‎ 3‎ ‎4、用标杆长度减去人的身高，即DE的长度。‎ ‎5、由DE∥AB得△KDE∽△KAB。又因为相似三角形三边对应成比例，∴‎ ‎6、再将刚才测量的数值代入比例式中，计算出AB的长度。‎ ‎7、用AB加上人的身高即得出大楼的高度。‎ 探究点拔：‎ ‎1.选择测量的方法应是切实可行的。如本题中人眼、杆顶、楼顶在一条直线上（人是站立的）。‎ ‎2．大楼的高度=AB+人高。‎ ‎3．测量的过程要清楚，力求每步都有根有据，达到学以至用。‎ 实例分析：‎ 例1、如图所示，站在离旗杆BE底部10米处的D点，目测旗杆的顶部，视线AB与水平线的夹角∠BAC=34°，并已知目高AD为1米。现在请你按1：500的比例得△ABC画在纸上，并记为△A1B1C1,用刻度尺量出纸上B1C1的长度，便可以算出旗杆的实际高度。你知道计算的方法吗？‎ ‎【随堂练习】‎ ‎1．已知在△ABC中，∠A=30°，AB=‎1米，现要用1：100的比例尺把△ABC画在纸上记作△A′B′C′，那么A′B′=________，∠A′=______．‎ ‎2．在某时刻的阳光照耀下，身高‎160cm的阿美的影长为‎80cm，她身旁的旗杆影长‎10m，则旗杆高为_______m．‎ ‎3．在比例尺是1：38000的某交通游览图上，某隧道长约‎7cm，它的实际长度约为（ ）‎ A．‎0.266km B．‎2.66km C．‎26.6km D．‎‎266km 3‎ ‎4．如图1，雨后初晴，一学生在运动场上玩耍，他的身高为AB，从他前面不远的一小块积水处，他看到了旗杆顶端的倒影C点，于是他向前走了两步，到达积水处，又继续向前走，到达旗杆底部时他共走了18步（假设他的步幅是不变的），已知他眼部A点高‎1.5m，则旗杆DE的高度为多少？（学生一步长为‎1m）‎ 解：由题意得△ABC∽△DEC．‎ ‎∴ ①‎ ‎∴DE=21，∴旗杆DE高度为21m． ②‎ ‎（1）上述解题过程有无错误？如有，错在第______步，错误原因是________．‎ ‎（2）请写出正确解题的过程．‎ ‎【中考连线】‎ 如图，小明要测量河内小岛B到河边公路l的距离，在A点测得，在C点测得，又测得米，则小岛B到公路l的距离为（ ）米．‎ A．25 B． C． D．‎ 答案：‎ 随堂练习 ‎1．1厘米 35° 2．20 3．B ‎4．（1）② 相似三角形对应边对应错误 ‎（2）正确解答：由题意得△ABC∽△DEC．,∴DE=12．‎ 中考连线 B 3‎