2020九年级数学上册 第二十一章实际问题与一元二次方程

2020九年级数学上册 第二十一章实际问题与一元二次方程

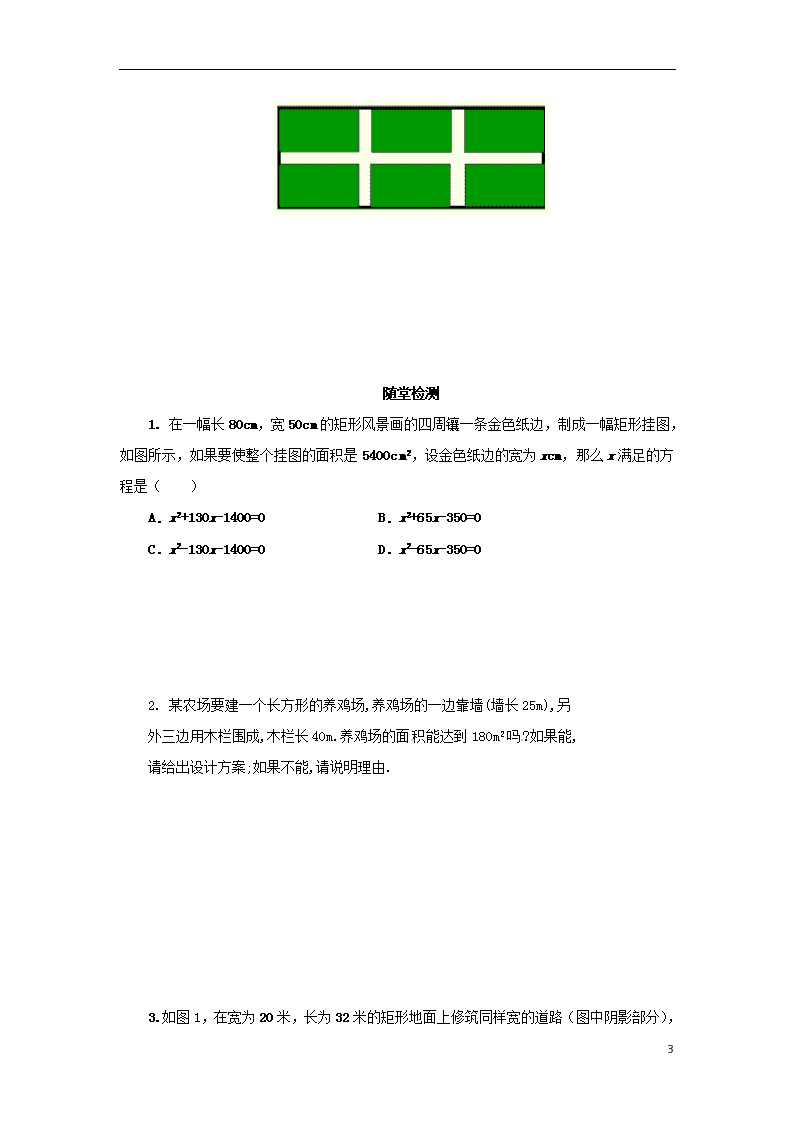
‎21.3实际问题与一元二次方程 第3课时 一、学习目标：‎ ‎1、能根据具体问题中的数量关系，列出一元二次方程，体会方程是刻画现实世界的一个有效的数学模型；‎ ‎2、能根据问题的实际意义，检验所得结果是否合理；‎ ‎3、进一步掌握列方程解应用题的步骤和关键.‎ 二、学习重难点：‎ 重点：列一元二次方程解决几何面积问题等 难点：掌握列方程解应用题的步骤和关键 探究案 三、合作探究 复习引入 某小区规划在一个长30m、宽20m的长方形土地上修建三条等宽的通道，使其中两条与AB平行，另外两条与AD平行，其余部分种花草，要使每一块花草的面积都为78m2，那么通道宽应该设计为多少？设通道宽为xm，则由题意列的方程为_______________________.‎ 活动1：‎ 问题1：要设计一本书的封面，封面长 27 cm，宽 21 cm，正中央是一个矩形，如果要使四周的彩色边衬所占面积是封面面积的四分之一，上、下、左、右边衬等宽，应如何设计四周边衬的宽度？ ‎ 思考：（1）本题中有哪些数量关系？‎ ‎（2）如何利用已知的数量关系选取未知数并列出方程？‎ 7‎ 活动2：‎ 问题2：要设计一本书的封面，封面长 27 cm，宽 21 cm，正中央是一个与整个封面长宽比例相同的矩形，如果要使四周的彩色边衬所占面积是封面面积的四分之一，上、下边衬等宽，左、右边衬等宽，应如何设计四周边衬的宽度（结果保留小数点后一位） ？‎ 思考：（1）本题中有哪些数量关系？‎ ‎（2）正中央是一个与整个封面长宽比例相同的矩形如何理解？‎ ‎（3）如何利用已知的数量关系选取未知数并列出方程？‎ 思考：如果换一种设未知数的方法，是否可以更简单地解决上面的问题？请你试一试．‎ 活动3：典例精析 例题:如图是宽为20米,长为32米的矩形耕地,要修筑同样宽的三条道路(两条纵向,一条横向,且互相垂直),把耕地分成六块大小相等的试验地,要使试验地的面积为570平方米,问:道路宽为多少米?‎ 7‎ 随堂检测 ‎1. 在一幅长‎80cm，宽‎50cm的矩形风景画的四周镶一条金色纸边，制成一幅矩形挂图，如图所示，如果要使整个挂图的面积是‎5400cm2，设金色纸边的宽为xcm，那么x满足的方程是（ ）‎ A．x2+130x-1400=0 B．x2+65x-350=0‎ C．x2-130x-1400=0 D．x2-65x-350=0‎ ‎2. 某农场要建一个长方形的养鸡场,养鸡场的一边靠墙(墙长‎25m),另 外三边用木栏围成,木栏长40m.养鸡场的面积能达到180m2吗?如果能,‎ 请给出设计方案;如果不能,请说明理由.‎ ‎3. 如图1，在宽为‎20米，长为‎32米 7‎ 的矩形地面上修筑同样宽的道路（图中阴影部分），余下的部分种上草坪．要使草坪的面积为540平方米，求道路的宽.‎ ‎4.如图，有长为‎24米的篱笆，一面利用墙（墙的最大可用长度a为‎10米），围成中间隔有一道篱笆的长方形花圃。设花圃的宽AB为x米，面积为S米2，‎ ‎（1）求S与x的函数关系式;‎ ‎（2）如果要围成面积为45米2的花圃，AB的长是多少米？‎ 7‎ ‎5. 有一张长6尺，宽3尺的长方形桌子，现用一块长方形台布铺在桌面上，如果台布的面积是桌面面积的2倍，且四周垂下的长度相同，试求这块台布的长和宽各是多少？（精确到0.1尺）‎ ‎6. 某种服装进价每件60元，据市场调查，这种服装按80元销售时，每月可卖出400件，若销售价每涨1元，就要少卖出5件，如果服装店预计在销售这种服装时每月获利12000元，那么这种服装的销售价应定为多少时，可使顾客更实惠？‎ 课堂小结 通过本节课的学习在小组内谈一谈你的收获，并记录下来：‎ 我的收获 ‎__________________________________________________________________________________________________________________________________________________________‎ 7‎ 参考答案 情境导入 ‎(30-2x)(20-x)=6×78‎ 课堂探究 问题1：解：可设四周边衬的宽度为 x cm，则中央矩形的面积可以表示为(27 - 2x)(21 - 2x)‎ 则，可列方程为：‎ 或 解得 问题2：解：设上、下边衬的宽均为 9y cm，左、右边衬的宽均为 7y cm，依题意，得 解方程，得 ‎≈‎1.8 cm， ≈‎‎1.4 cm 答：上、下边衬的宽均为1.8 cm，左、右边衬的宽均为 1.4 cm 例题解析 解:设道路宽为x米，则 化简，得 其中的 x=35超出了原矩形的宽，应舍去.‎ 答:道路的宽为1米.‎ 随堂检测 ‎1.B ‎2. 解:设养鸡场的长为xm,根据题意得: ‎ 即 x2 - 40x + 360=0.‎ 解方程,得x1 = x2= (舍去),‎ 7‎ 答：鸡场的为（）m满足条件.‎ ‎3. 解：设道路宽为x米，由平移得到图2，则宽为(20-x)米，长为（32-x)米，列方程得 ‎（20-x)(32-x)=540，‎ 整理得 x2-52x+100=0，‎ 解得 x1=50(舍去），x2=2.‎ 答：道路宽为2米.‎ ‎4. 解：(1)设宽AB为x米，则BC为(24-3x)米，这时面积 S=x(24-3x)=-3x2+24x.‎ ‎(2)由条件-3x2+24x=45‎ 化为：x2-8x+15=0.‎ 解得 x1=5，x2=3.‎ ‎∵由0＜24-3x≤10，得14/3≤x＜8，‎ ‎∴x2不合题意，AB=5，即花圃的宽AB为5米.‎ ‎5. 解：设四周垂下的宽度为x尺，则台布的长为（2x+6）尺，宽为（2x+3）尺，依题意得：（6+2x）（3+2x）=2×6×3‎ ‎ 整理方程得：2x²+9x-9=0‎ ‎ 解得：x1≈0.84，x2≈-5.3（不合题意，舍去）‎ ‎ 即这块台布的长约为7.7尺，宽约为4.7尺.‎ ‎6. 解：设销售价提高了x个1元，则每月应少卖出5x件， 依题意可列方程：（80+x-60）×（400-5x）=12000‎ ‎ 解方程得：x1=20，x2=40‎ ‎ 显然，当x=40时，销售价为120元； 当x=20时，销售价为100元，‎ ‎ 要使顾客得到实惠，则销售价越低越好，故这种服装的销售价应定为100元合适。‎ 7‎