中考数学 动态几何中的面积问题复习

中考数学 动态几何中的面积问题复习

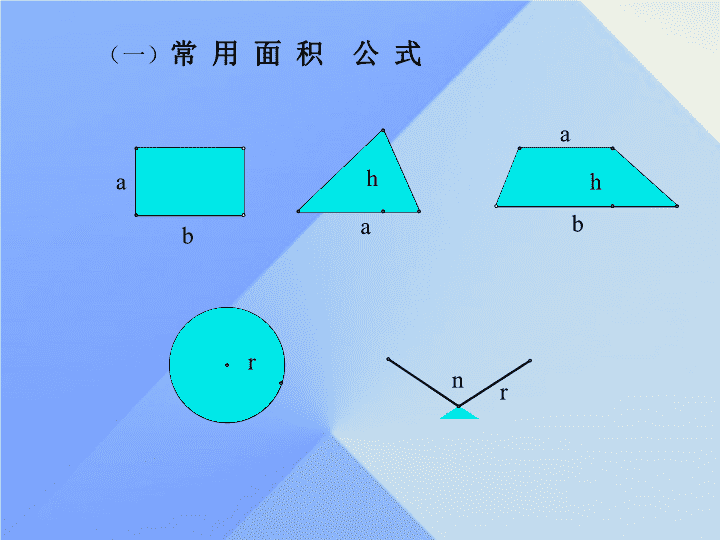
动态几何题中面积 -------- 中考 复习课 （一） 常 用 面 积 公 式 a b h a h b a r n r 例 1. 当汽车在 雨天行驶时 , 为了看清道路 , 司机要启动前方挡风玻璃上的雨刷器 , 怎样求雨刷扫过的面积呢 ? 趣味数学 • 生活在线 小明仔细观察了雨刷器的转动情况 , 量得 CD=90cm, ∠DBA=20°, 端点 C.D 与点 A 的距离分别为 115cm,35cm, 他经过思考只选用其中的 部分数据 就求得结果 , 你知道小明是怎样计算的吗 ? 也请你算一算雨刷 CD 扫过的面积 ? 生活与数学转化 在旋转问题中 , 常常把不规则图形通过 割补的方法 转化为规则图形 C D A B A B D E C B F C E D A 10 6 s (1) 折一折，算一算 探究示例 • 课堂在线 ( 一 ) 求 △ CEF 的面积 ? 例 2. 如图 , 将矩形 ABCD 沿着直线 BD 折叠 , 使点 C 落在 C / 处 , BC / 交 AD 于点 E, AD=8,AB=4,求△ BED 的面积 . 探究点拨 : （ 1 ）求重叠部分的面积先确定重叠部分的形状 (2) 翻折后的三角形与原三角形成轴对称 . ( 两个三角形全等 ), (3) 对称轴是折痕所在的直线 . (4) 列方程求边长 . 探究示例 • 课堂在线 ( 二 ) 8-x 4 x x E 8 4 例 3. 用一边长为 5 厘米的正方形 ABCD 和等腰 △ PQR, PQ=PR=5cm,QR=8cm, 点 B 、 C 、 Q 、 R 在同一直线上 , 当 C 、 Q 两点重合时 , 等腰 △ PQR 以 1 厘米 / 秒的速度沿着直线 I 向左开始平移， 直到 C 与 R 两点重合为止 . 设 t 秒后正方形 ABCD 与等腰 △ PQR 重叠部分的面积为 S 厘米 2 ，求 S 与 t 的函数关系式。 探究示例 • 课堂在线 ( 三 ) 5 5 8 5 E (1) 0≤t≤4 (2) 4 ＜ t≤5 E (3) 5 ＜ t≤8 E 在动态几何题中求面积的感想： 观察问题：全面化（ 从 表面为变化全 过程） 思考问题 ：多面化（ 从 静态一面转化为动态多面） 解决问题 ：分类化（ 要分类讨论） 有效途径 ： 动手操作 1.(2005 中考题 ) 如图所示，∠ C 为直角三角形△ ABC 中的直角， AB=5cm,BC=4cm,AC=3cm. 将三角形 折成 AC 边与 AB 边重叠，点 C 与 C / 重合，求△ B C / D 的面积。 C B A B A C D C / 热点聚焦 • 中 考 在 线 ( 一 ) 2. 如图，△ ABC 中，∠ C 是直角， AB=12cm, ∠ABC=60°, 将△ ABC 以点 B 为中心顺时针旋转， 使点 C 旋转到边 AB 的 延长线上的 D 处，求边 AC 扫过的图形（阴影部分）的面积 60° 热点聚焦 • 中 考 在 线 ( 二 ) 3. 如图 , 在 Rt △PMN 中, ∠P=90° , PM=PN, MN=8cm, 矩形 ABCD 的长和宽分别为 8cm 和 2cm,C 点和 M 点重合 ,BC 和 MN 在一条直线上 , 令 Rt △PMN 不动 , 矩形 ABCD 沿 MN 所在的直线向右以 1cm/ 每秒 的速度平移 , 直到 C 点与 N 点重合为止 , 设移动 x 秒后 , 矩形 ABCD 与 △ PMN 的重叠部分的面积为 y, 求 y 与 x 之间的函数关系式 . 热点聚焦 • 中 考 在 线 ( 三 ) 8cm 8cm 2cm 课堂聚焦 一个或几个几何图形在翻折、旋转和平移运动中面积的求法注意点： ★ 把握运动和变化的全过程； ★ 关注运动与变化中的不变量、不变关系和特殊系； ★ 综合运用方程、分类讨论、函数、三角形相似和图形结合的思想 。