相似三角形的性质和判定教案(1)

相似三角形的性质和判定教案(1)

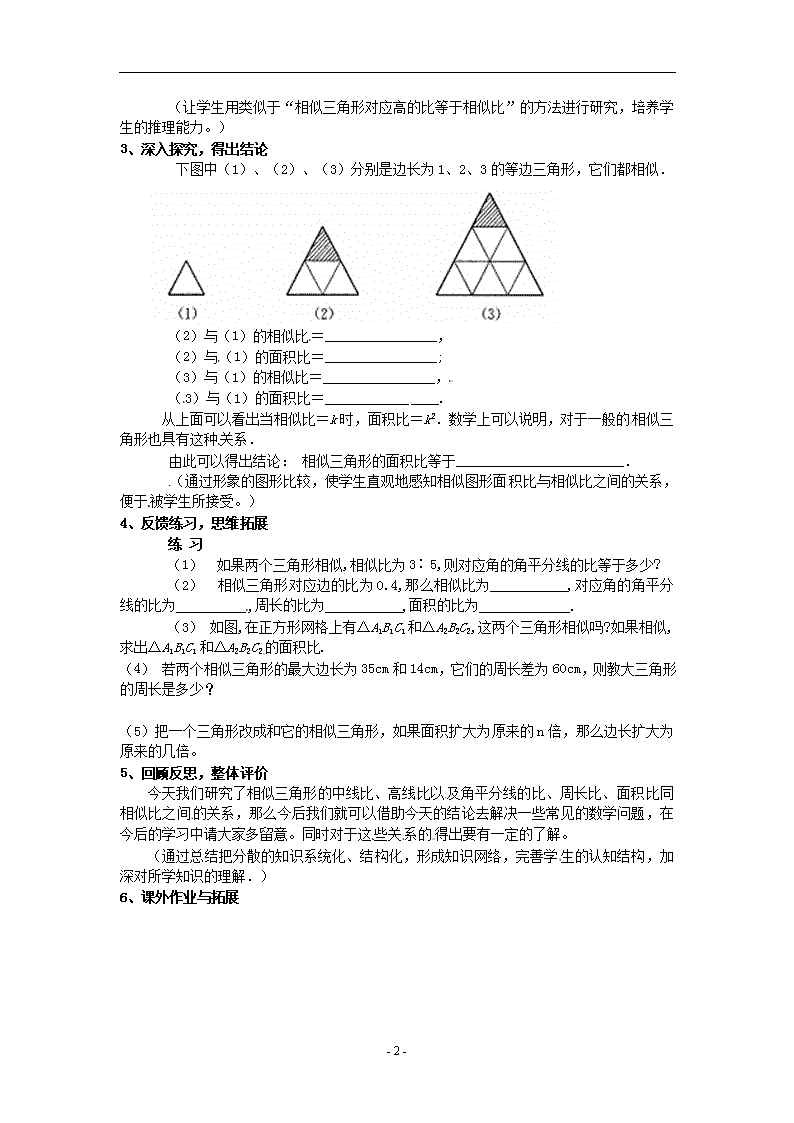
‎3.3相似三角形的性质和判定（一）‎ 一、教学目标 ‎1.利用前面几节的相关结论经过简单的推导得出相似三角形的各条性质；‎ ‎2.运用相似三角形性质解决简单的问题。‎ 二、教学重难点 教学重点：相似三角形的各条性质的掌握 教学难点：相似三角形性质中面积比的结论的得出。‎ 三、教学过程设计 ‎1、创设情境，设疑激趣 两个三角形相似，除了对应边成比例、对应角相等之外，还可以得到许多有用的结果．例如，在图1中，△ABC和△A′B′C′是两个相似三角形，相似比为k，其中AD、A′D′分别为BC、B′C′边上的高，那么AD、 A′D′之间有什么关系？‎ ‎2、探索研究，形成新知 ‎△ABD和△A′B′D′都是直角三角形，而∠B＝∠B′，因为有两个角对应相等，所以这两个三角形相似．那么 ‎ ‎ 由此可以得出结论： 相似三角形对应高的比等于相似比．‎ ‎   （通过研究讨论，让学生借助已有的知识对新问题进行研究，培养学生的思考探索能力，同时让他们自己得出结论，感受成功的喜悦。）‎ 思 考 ‎    下图中，△ABC和△A′B′C′相似，AD、A′D′分别为对应边上 的中线，BE、B′E′分别为对应角的角平分线，那么它们之间有什么关系呢？‎ ‎    可以得到的结论是_________________________________________．‎ ‎    想一想： 两个相似三角形的周长比是什么？‎ ‎    可以得到的结论是_________________________________________．‎ - 2 -‎ ‎    （让学生用类似于“相似三角形对应高的比等于相似比”的方法进行研究，培养学生的推理能力。）‎ ‎3、深入探究，得出结论 ‎ 下图中（1）、（2）、（3）分别是边长为1、2、3的等边三角形，它们都相似．‎ ‎    （2）与（1）的相似比＝________________，‎ ‎    （2）与（1）的面积比＝________________;‎ ‎    （3）与（1）的相似比＝________________，‎ ‎    （3）与（1）的面积比＝________________.‎ ‎    从上面可以看出当相似比＝k时，面积比＝k2．数学上可以说明，对于一般的相似三角形也具有这种关系．‎ ‎    由此可以得出结论： 相似三角形的面积比等于________________________．‎ ‎    （通过形象的图形比较，使学生直观地感知相似图形面积比与相似比之间的关系，便于被学生所接受。）‎ ‎4、反馈练习，思维拓展 练 习 ‎（1） 如果两个三角形相似,相似比为3∶5,则对应角的角平分线的比等于多少?‎ ‎（2） 相似三角形对应边的比为0.4,那么相似比为___________,对应角的角平分线的比为__________,周长的比为___________,面积的比为_____________.‎ ‎（3） 如图,在正方形网格上有△A1B1C1和△A2B2C2,这两个三角形相似吗?如果相似,求出△A1B1C1和△A2B2C2的面积比.‎ ‎（4） 若两个相似三角形的最大边长为35cm和14cm，它们的周长差为60cm，则教大三角形的周长是多少？‎ ‎（5）把一个三角形改成和它的相似三角形，如果面积扩大为原来的n倍，那么边长扩大为原来的几倍。‎ ‎5、回顾反思，整体评价 今天我们研究了相似三角形的中线比、高线比以及角平分线的比、周长比、面积比同相似比之间的关系，那么今后我们就可以借助今天的结论去解决一些常见的数学问题，在今后的学习中请大家多留意。同时对于这些关系的得出要有一定的了解。‎ ‎（通过总结把分散的知识系统化、结构化，形成知识网络，完善学生的认知结构，加深对所学知识的理解．）‎ ‎6、课外作业与拓展 - 2 -‎