2011年全国各地100份中考数学试卷分类汇编第22--全等三角形

2011年全国各地100份中考数学试卷分类汇编第22--全等三角形

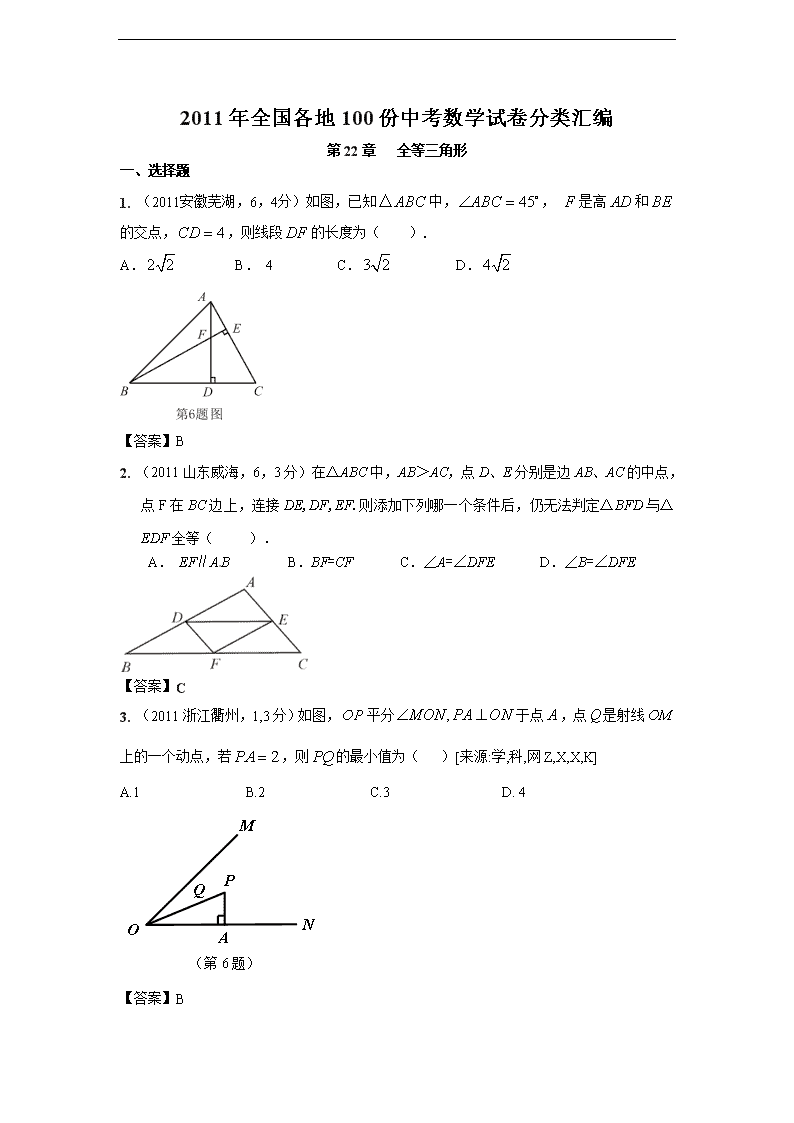
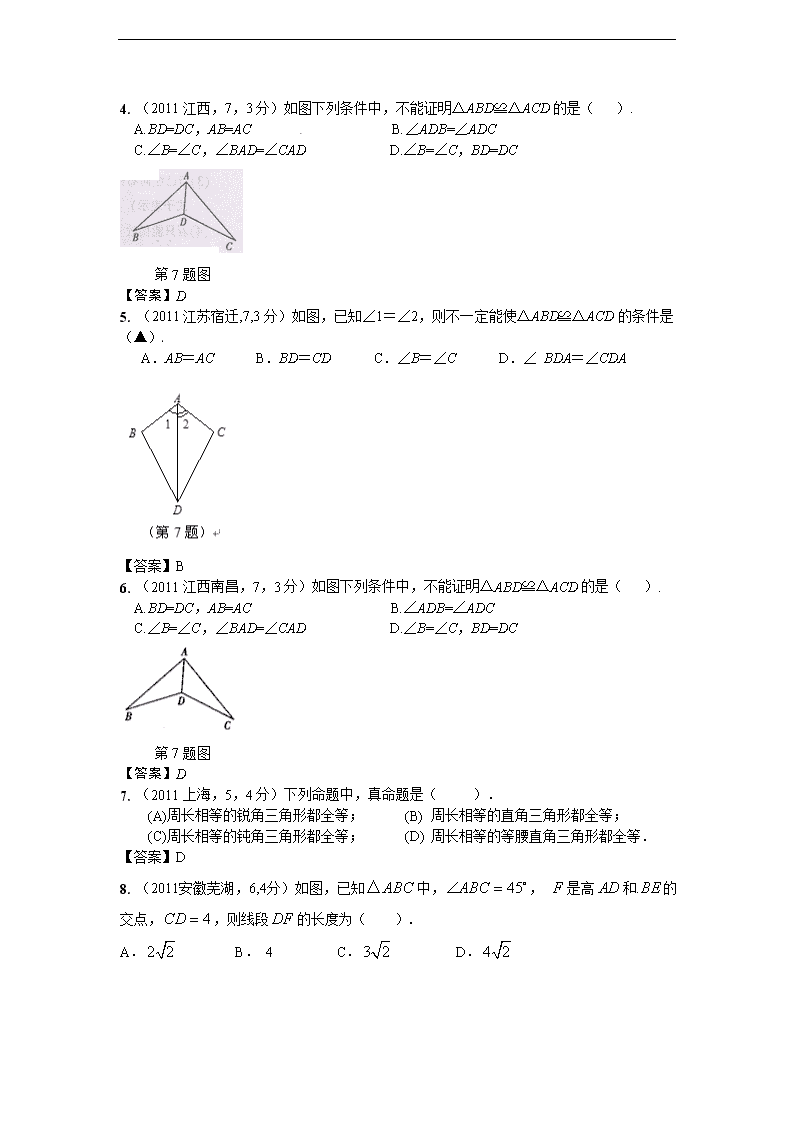
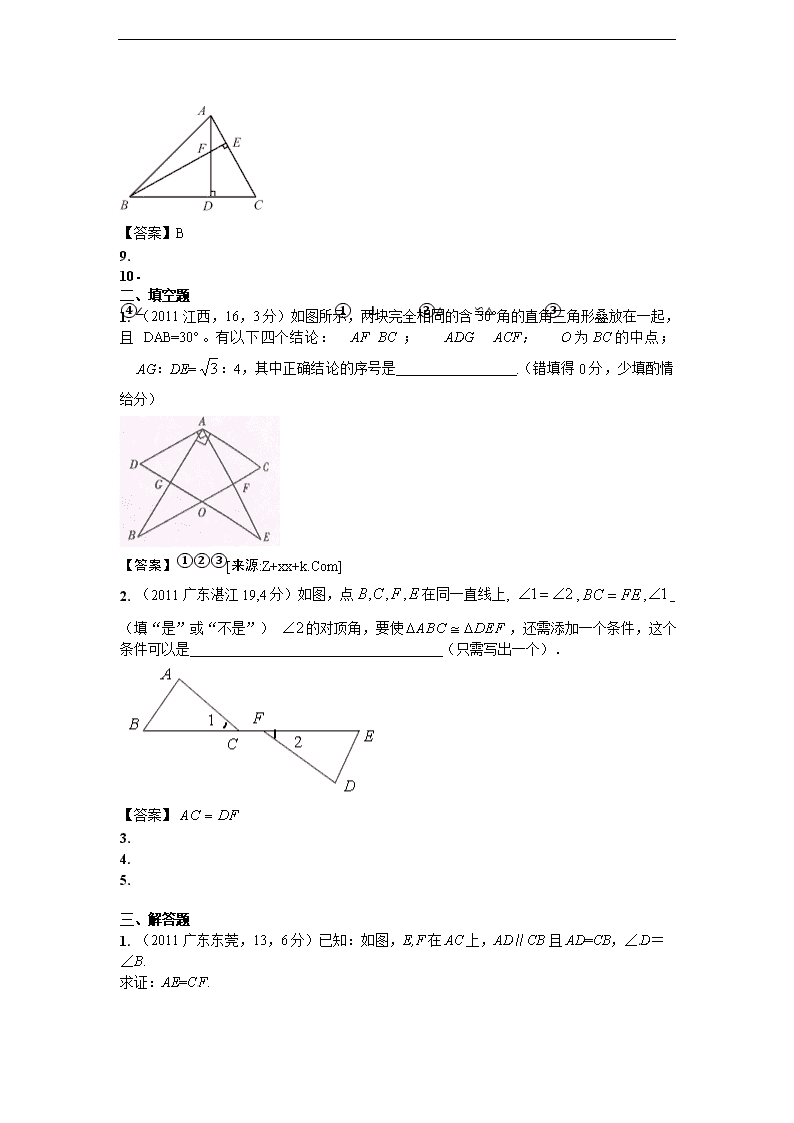
‎2011年全国各地100份中考数学试卷分类汇编 第22章 全等三角形 一、选择题 ‎1. （2011安徽芜湖，6，4分）如图，已知中，， 是高和的交点，，则线段的长度为（ ）. ‎ A． B． ‎4 ‎C． D．‎ ‎【答案】B ‎2. （2011山东威海，6，3分）在△ABC中，AB＞AC，点D、E分别是边AB、AC的中点，点F在BC边上，连接DE,DF,EF.则添加下列哪一个条件后，仍无法判定△BFD与△EDF全等（ ）．‎ A． EF∥AB B．BF=CF C．∠A=∠DFE D．∠B=∠DFE ‎ ‎【答案】C ‎3. （2011浙江衢州，1,3分）如图，平分于点，点是射线上的一个动点，若，则的最小值为（ ）[来源:学,科,网Z,X,X,K]‎ A.1 B‎.2 C.3 D. 4‎ ‎（第6题）‎ ‎【答案】B ‎4. （2011江西，7，3分）如图下列条件中，不能证明△ABD≌△ACD的是（ ）.‎ A.BD=DC，AB=AC B.∠ADB=∠ADC ‎ C.∠B=∠C，∠BAD=∠CAD D.∠B=∠C，BD=DC 第7题图 ‎【答案】D ‎5. （2011江苏宿迁,7,3分）如图，已知∠1＝∠2，则不一定能使△ABD≌△ACD的条件是（▲）‎ A．AB＝AC B．BD＝CD C．∠B＝∠C D．∠ BDA＝∠CDA ‎【答案】B ‎6. （2011江西南昌，7，3分）如图下列条件中，不能证明△ABD≌△ACD的是（ ）.‎ A.BD=DC，AB=AC B.∠ADB=∠ADC ‎ C.∠B=∠C，∠BAD=∠CAD D.∠B=∠C，BD=DC 第7题图 ‎【答案】D ‎7. （2011上海，5，4分）下列命题中，真命题是（ ）．‎ ‎(A)周长相等的锐角三角形都全等； (B) 周长相等的直角三角形都全等；‎ ‎(C)周长相等的钝角三角形都全等； (D) 周长相等的等腰直角三角形都全等．‎ ‎【答案】D ‎8. （2011安徽芜湖，6,4分）如图，已知中，， 是高和的交点，，则线段的长度为（ ）. ‎ A． B． ‎4 ‎C． D．‎ ‎【答案】B ‎9. ‎ ‎10．‎ 二、填空题 ‎1. （2011江西，16，3分）如图所示，两块完全相同的含30°角的直角三角形叠放在一起，且∠DAB=30°。有以下四个结论：①AF⊥BC ；②△ADG≌△ACF； ③O为BC的中点； ④AG：DE=：4，其中正确结论的序号是 .（错填得0分，少填酌情给分）‎ ‎【答案】①②③[来源:Z+xx+k.Com]‎ ‎2. （2011广东湛江19,4分）如图，点在同一直线上, ,, ‎ ‎（填“是”或“不是”） 的对顶角，要使，还需添加一个条件，这个条件可以是 （只需写出一个）．‎ ‎【答案】‎ ‎3. ‎ ‎4. ‎ ‎5. ‎ 三、解答题 ‎1. （2011广东东莞，13，6分）已知：如图，E,F在AC上，AD∥CB且AD=CB，∠D＝∠B.‎ 求证：AE=CF.‎ ‎【答案】∵AD∥CB ‎∴∠A=∠C 又∵AD=CB，∠D=∠B ‎∴△ADF≌△CBE ‎∴AF=CE ‎∴AF+EF=CE+EF 即AE=CF ‎2. （2011山东菏泽，15（2），6分）已知：如图，∠ABC=∠DCB，BD、CA分别是∠ABC、∠DCB的平分线．求证：AB=DC 证明：在△ABC与△DCB中 ‎ （∵AC平分∠BCD，BD平分∠ABC） ‎ ‎∴△ABC≌△DCB ‎ ‎∴AB=DC ‎ ‎3. （2011浙江省，19，8分）如图，点D，E分别在AC，AB上．‎ ‎(1) 已知，BD=CE，CD=BE，求证：AB=AC；‎ ‎(2) 分别将“BD=CE”记为①，“CD=BE” 记为②，“AB=AC”记为③．添加条件①、③，以②为结论构成命题1，添加条件②、③以①为结论构成命题2．命题1是命题2的 命题，命题2是 命题．（选择“真”或“假”填入空格）．‎ ‎【答案】(1) 连结BC，∵ BD=CE，CD=BE，BC=CB．‎ ‎∴ △DBC≌△ECB （SSS）‎ ‎∴ ∠DBC =∠ECB ‎∴ AB=AC ‎(2) 逆， 假；‎ ‎4. （2011浙江台州，19,8分）如图，在□ABCD中，分别延长BA，DC到点E，使得AE=AB，CH=CD，连接EH，分别交AD，BC于点F,G。求证：△AEF≌△CHG.‎ ‎【答案】证明： ∵ □ABCD ‎∴ AB=CD,∠BAD=∠BCD AB∥CD ‎∴ ∠EAF=∠HCG ∠E=∠H ‎∵ AE=AB，CH=CD ‎∴ AE=CH ‎∴ △AEF≌△CHG.‎ ‎5. （2011四川重庆，19，6分）如图，点A、F、C、D在同一直线上，点B和点E分别在直线AD的两侧，且AB＝DE，∠A＝∠D，AF＝DC．求证：BC∥EF．[来源:Zxxk.Com]‎ ‎【证明】∵AF＝DC，∴AC＝DF，又∠A＝∠D ，‎ AB＝DE，∴△ABC≌△DEF，‎ ‎∴∠ACB＝∠DFE，∴BC∥EF．‎ ‎6. （2011江苏连云港，20，6分）两块完全相同的三角形纸板ABC和DEF，按如图所示的方式叠放，阴影部分为重叠部分，点O为边AC和DF的交点.不重叠的两部分△AOF与△DOC是否全等？为什么？‎ ‎【答案】解：全等 .理由如下：∵两三角形纸板完全相同，∴BC=BF，AB=BD，∠A=∠D，∴AB－BF=BD－BC，即AF=DC.在△AOF和△DOC中，∵AF=DC，∠A=∠D，∠AOF=∠DOC，∴△AOF≌△DOC（AAS）.‎ ‎7. （2011广东汕头，13，6分）已知：如图，E,F在AC上，AD∥CB且AD=CB，∠D＝∠B.‎ 求证：AE=CF.‎ ‎【答案】∵AD∥CB ‎∴∠A=∠C 又∵AD=CB，∠D=∠B ‎∴△ADF≌△CBE ‎∴AF=CE ‎∴AF+EF=CE+EF 即AE=CF ‎8. （ 2011重庆江津， 22，10分）在△ABC中,AB=CB,∠ABC=90º,F为AB延长线上一点,点E在BC上,且AE=CF.‎ ‎ (1)求证:Rt△ABE≌Rt△CBF;‎ ‎(2)若∠CAE=30º,求∠ACF度数.‎ A B C E F 第22题图 ‎【答案】（1）∵∠ABC=90°,∴∠CBF=∠ABE=90°.‎ 在Rt△ABE和Rt△CBF中,‎ ‎∵AE=CF, AB=BC, ∴Rt△ABE≌Rt△CBF(HL)‎ ‎(2)∵AB=BC, ∠ABC=90°, ∴ ∠CAB=∠ACB=45°.‎ ‎∵∠BAE=∠CAB-∠CAE=45°-30°=15°.‎ 由（1）知 Rt△ABE≌Rt△CBF， ∴∠BCF=∠BAE=15°,‎ ‎∴∠ACF=∠BCF+∠ACB=45°+15°=60°.‎ ‎9. （2011福建福州，17（1），8分）如图6,于点,于点,交于点,且.‎ 求证.‎ 图6‎ ‎[来源:学&科&网Z&X&X&K]‎ ‎【答案】(1)证明:∵,‎ ‎∴‎ 在和中[来源:Zxxk.Com]‎ ‎∴≌‎ ‎∴[来源:学*科*网]‎ ‎10．（2011四川内江，18，9分）如图，在Rt△ABC中，∠BAC=90°，AC=2AB，点D是AC的中点，将一块锐角为45°的直角三角板如图放置，使三角板斜边的两个端点分别与A、D重合，连结BE、EC．‎ 试猜想线段BE和EC的数量及位置关系，并证明你的猜想．‎ A B C D E ‎【答案】BE=EC，BE⊥EC ‎∵AC=2AB，点D是AC的中点 ‎∴AB=AD=CD ‎∵∠EAD=∠EDA=45°‎ ‎∴∠EAB=∠EDC=135°‎ ‎∵EA=ED ‎∴△EAB≌△EDC ‎∴∠AEB=∠DEC，EB=EC ‎∴∠BEC=∠AED=90°‎ ‎∴BE=EC，BE⊥EC ‎11. （2011广东省，13，6分）已知：如图，E,F在AC上，AD∥CB且AD=CB，∠D＝∠B.‎ 求证：AE=CF.‎ ‎【答案】∵AD∥CB ‎∴∠A=∠C 又∵AD=CB，∠D=∠B ‎∴△ADF≌△CBE ‎∴AF=CE ‎∴AF+EF=CE+EF[来源:Zxxk.Com]‎ 即AE=CF ‎12. （2011湖北武汉市，19，6分）（本题满分6分）如图，D，E，分 别 是 AB，AC 上 的 点 ，且AB=AC，AD=AE．求证∠B=∠C．‎ ‎【答案】证明：在△ABE和△ACD中，‎ AB＝AC ∠A＝∠A AE＝AD ‎     ∴△ABE≌△ACD ‎     ∴∠B=∠C ‎13. （2011湖南衡阳，21，6分）如图，在△ABC中，AD是中线，分别过点B、C作AD及其延长线的垂线BE、CF，垂足分别为点E、F．求证：BE=CF．‎ ‎【证明】∵在△ABC中，AD是中线，[来源:学科网ZXXK]‎ ‎∴BD=CD，∵CF⊥AD，BE⊥AD，∴∠CFD＝∠BED＝90° ，在△BED与△CFD中，∵∠BED＝∠CFD，∠BDE＝∠CDF，BD＝CD，∴△BED≌△CFD，∴BE=CF．‎ ‎14. (20011江苏镇江,22,5分)已知:如图,在△ABC中,D为BC上的一点,AD平分∠EDC,且∠E=∠B,ED=DC.‎ ‎[来源:学+科+网]‎ ‎[来源:学科网ZXXK]‎ 求证:AB=AC ‎【答案】证明∵AD平分∠EDC,∴∠ADE=∠ADC,又DE=DC,AD=AD,‎ ‎∴△ADE≌△ADC, ∴∠E=∠C,‎ 又∠E=∠B, ∴∠B =∠C, ∴AB=AC.‎ ‎15. （2011湖北宜昌，18，7分）如图，在平行四边形ABCD 中，E为BC 中点，AE的延长线与DC的延长线相交于点F.‎ ‎(1)证明：∠DFA = ∠FAB；‎ ‎(2)证明: △ABE≌△FCE.‎ ‎ （第18题图）‎ ‎【答案】证明：（1）∵AB与CD是平行四边形ABCD的对边，∴AB∥CD，（1分）∴∠F=∠FAB．（3分）（2）在△ABE和△FCE中， ∠FAB=∠F （4分）∵ ∠AEB=∠FEC （5分）BE=CE （6分）∴ △ABE≌△FCE．（7分）‎