2008年中考数学分类真理练习23圆的有关计算

2008年中考数学分类真理练习23圆的有关计算

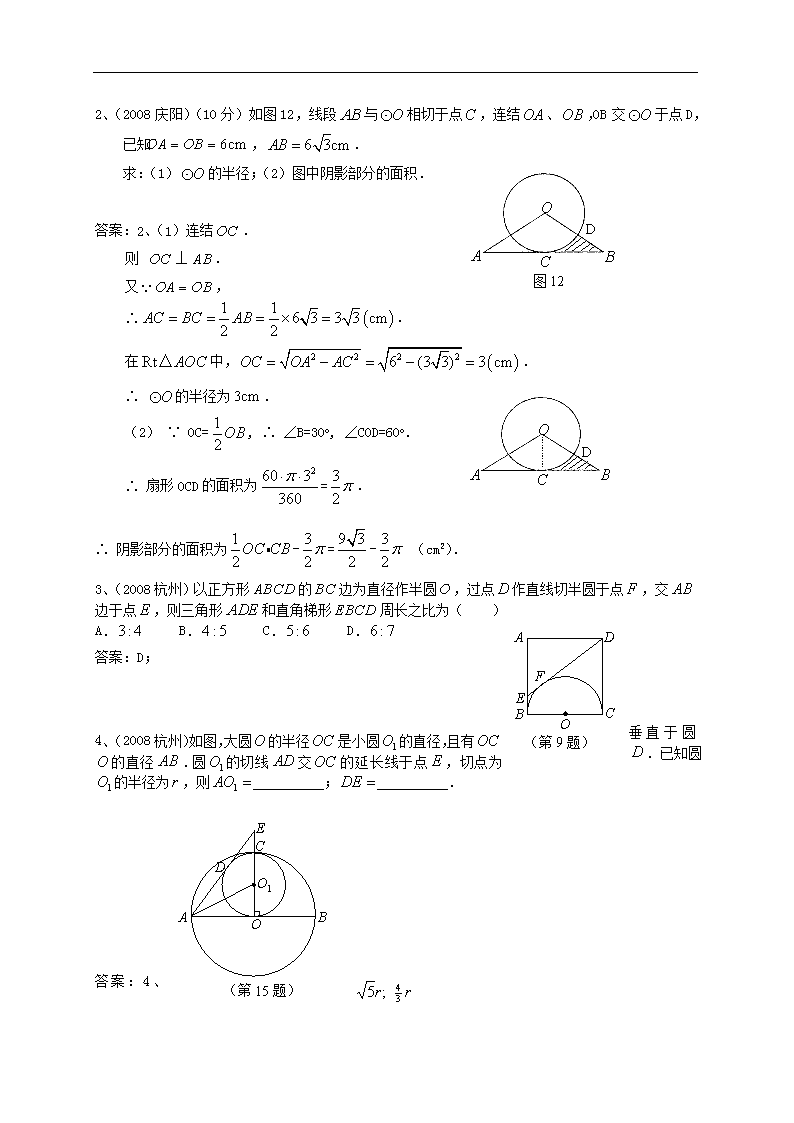
圆的有关计算 图7‎ ‎1、（2008庆阳）图7中外接圆的圆心坐标是　　　 　．‎ 答案：‎ 附加题：“图7中外接圆的圆心坐标是　　 　　．”‎ 请再求：（1) 该圆圆心到弦AC的距离；‎ ‎（2）以BC为旋转轴，将旋转一周所得几何体的全面积（所有表面面积之和）．‎ 图7‎ 答案：（1）方法1：‎ 如图，圆心为P（5，2），作PD⊥AC于D，则AD=CD．‎ D P 连结CP，∵ AC为是为6、宽为2的矩形的对角线，‎ ‎∴ AC==2．‎ 同理 CP==2．‎ ‎∴ PD==．‎ 方法2：‎ ‎∵ 圆心为P（5，2），作PD⊥AC于D，则AD=CD．‎ 由直观，发现点D的坐标为（2，3）．‎ 又∵ PD为是为3、宽为1的矩形的对角线，‎ ‎∴ PD==．‎ ‎ （2）‎ ‎∵ 旋转后得到的几何体是一个以2为底面圆半径、6为高的大圆锥，再挖掉一个以2为底面圆半径、2为高的小圆锥，‎ 又 它们的母线之长分别为小==，大==，‎ ‎∴ 所求的全面积为：大+小 ‎ =（大+小）‎ ‎=4（-）．‎ ‎2、（2008庆阳）（10分）如图12，线段与相切于点，连结、，OB交于点D，已知，． ‎ D 图12‎ 求：（1）的半径；（2）图中阴影部分的面积．‎ 答案：2、（1）连结．‎ 则 ． ‎ 又，‎ ‎∴．‎ 在中，．‎ D ‎∴ 的半径为． ‎ ‎（2） ∵ OC=, ∴ ∠B=30o, ∠COD=60o．‎ ‎∴ 扇形OCD的面积为=．‎ ‎∴ 阴影部分的面积为-=- （cm2）．‎ ‎3、（2008杭州）以正方形的边为直径作半圆，过点作直线切半圆于点，交边于点，则三角形和直角梯形周长之比为（ ）‎ A D C B O E F ‎（第9题）‎ A． B． C． D．‎ 答案：D；‎ ‎4、（2008杭州）如图，大圆的半径是小圆的直径，且有垂直于圆的直径．圆的切线交的延长线于点，切点为．已知圆的半径为，则 ； ．‎ D C E O1‎ O A B ‎（第15题）‎ 答案：4、‎ ‎（2008金华）7.如图, 已知CD为⊙O的直径，过点D的弦DE平行于半径OA,若∠D的度数是50o,则∠C的度数是（ ）‎ A.50o B. 40o C. 30o D.25o 答案D ‎（2008金华）9.某抗震蓬的顶部是圆锥形,这个圆锥的底面直径为‎10米,母线长为‎6米,为了防雨,需要在它的顶部铺上油毡,所需油毡的面积至少是（ ）‎ A‎.30米2 B‎.60米2 C.30‎米2 D‎.60‎米2‎ 答案C ‎（2008温州）O ‎（第14题图）‎ C B A 14．如图，的半径为5，弦，于，则的长等于 ．‎ 答案3‎ A B C O E D ‎（2008金华）20.如图, CD切⊙O于点D,连结OC, 交⊙O于点B,过点B作弦AB⊥OD，点E为垂足,已知⊙O的半径为10,sin∠COD=.‎ 求：（1）弦AB的长；‎ ‎（2）CD的长；‎ ‎（3）劣弧AB的长（结果保留三个有效数字, sin53.13o ≈0.8, ≈3.142）.‎ 答案 (1)∵ AB⊥OD， ∴∠OEB=900‎ 在Rt△OEB中，BE=OB×sin∠COD=10×=8 ‎ 由垂径定理得AB=2BE=16 所以弦AB的长是16 ‎ ‎(2)方法（一） ‎ 在Rt△OEB中， OE= =6.‎ ‎∵CD切⊙O于点D, ∴∠ODC=900, ∴∠OEB=∠ODC.‎ ‎∵∠BOE=∠COD, ∴△BOE∽△COD, ‎ ‎∴ , ∴ , ∴CD= . 所以CD的长是 ‎ 方法（二）由sin∠COD= 可得tan∠COD= , ‎ 在Rt△ODC中，tan∠COD= , ∴CD=OD•tan∠COD=10×= ‎ ‎(3)连结OA. 在Rt△ODC中， ∵sin53.13o ≈0.8 ∴∠DOC=53.13o ‎ ‎∴∠AOB=106.26o ， ‎ ‎∴劣弧AB的长度 ≈18.5 ‎ ‎1、（2008 绍兴）如图，量角器外缘边上有三点，它们所表示的读数分别是，，，则的大小为（ ）‎ A． B． C． D．‎ 答案：B ‎2、（2008 绍兴）如图，轮椅车的大小两车轮（在同一平面上）与地面的触点 间距离为80cm，两车轮的直径分别为136cm，16cm，则此两车轮的圆心相距 cm．‎ ‎（第2题图）‎ A B ‎ 答案：100 ‎ ‎3、（2008 绍兴）如图中的圆均为等圆，且相邻两圆外切，圆心连线构成正三角形，记各阴影部分面积从左到右依次为，，，…，，则的值等于 ．‎ ‎（第3题图）‎ ‎（n+1）个图 答案：‎ ‎4、（2008 嘉兴）如图，直角坐标系中，已知两点，点在第一象限且为正三角形，的外接圆交轴的正半轴于点，过点的圆的切线交轴于点．‎ ‎（1）求两点的坐标；‎ ‎（2）求直线的函数解析式；‎ ‎（3）设分别是线段上的两个动点，且平分四边形的周长．‎ 试探究：的最大面积？‎ ‎（第4题）‎ 解：（1），．‎ 作于，‎ ‎（第4题）‎ 为正三角形，‎ ‎，．‎ ‎．‎ 连，，，‎ ‎．‎ ‎（第4题）‎ ‎．‎ ‎（2），是圆的直径，‎ 又是圆的切线，．‎ ‎，．‎ ‎．‎ 设直线的函数解析式为，‎ 则，解得．‎ 直线的函数解析式为．‎ ‎（3），，，，‎ 四边形的周长．‎ 设，的面积为，‎ 则，．‎ ‎．‎ 当时，．‎ 点分别在线段上，‎ ‎，解得．‎ 满足，‎ 的最大面积为．‎ 图15‎ ‎(2008甘肃白银)图15是一盒刚打开的“兰州”牌香烟，图16(1)是它的横截面（矩形ABCD），已知每支香烟底面圆的直径是‎8mm．‎ ‎(1) 矩形ABCD的长AB= mm；‎ ‎（2）利用图16(2)求矩形ABCD的宽AD．‎ ‎（≈1.73，结果精确到‎0.1mm）‎ ‎ ‎ ‎(1)‎ O1‎ O2‎ O3‎ 图16‎ ‎（2）‎ O1‎ O2‎ O3‎ D 解：(1)56；‎ ‎（2）如图，△O1 O2 O3是边长为‎8mm的正三角形，‎ 作底边O2O3上的高O1 D．则 O1D=O1O3·sin60°=4≈6.92． ‎ ‎∴ AD=2(O1D+4)=2×10.92≈21.8（mm）．‎ ‎（2008甘肃兰州）如图4，现有一个圆心角为90°，半径为‎8cm的扇形纸片，用它恰好围成一个圆锥的侧面（接缝忽略不计），则该圆锥底面圆的半径为（ C ）‎ A．‎4cm B．‎3cm C．‎2cm D．‎‎1cm 图4‎ ‎1．（2008齐齐哈尔T4）如图，小明想用图中所示的扇形纸片围成一个圆锥，已知扇形的半径为‎5cm，弧长是 O B AB 第1题图 ‎5cm cm，那么围成的圆锥的高度是 cm．‎ ‎4．4‎ ‎2. （2008哈尔滨市T7）如图，圆锥形烟囱帽的底面直径为‎80cm，母线长为‎50cm，则这样的烟囱帽的侧面 积是（ ）．‎ ‎（A）4000πcm2 （B）3600πcm2‎ ‎（C）2000πcm2 （D）1000πcm2‎ ‎7．C ‎1.（2008山东济南）已知：如图2，，在射线AC上顺次截取AD=‎3cm，DB=‎10cm，以DB为直径作⊙O交射线AP于E、F两点，求圆心O到AP的距离及EF的长．‎ 第19题图2‎ O A D B C E　　　　　　　　　　　　　　‎ F P Ｇ ‎（2）解：过点O作OG⊥AP于点G 连接OF 4分 ‎ ‎∵ DB=10，∴ OD=5‎ ‎∴ AO=AD+OD=3+5=8‎ ‎∵∠PAC=30°‎ ‎∴ OG=AO=cm 5分 ‎ ‎∵ OG⊥EF，∴ EG=GF ‎∵ GF= ‎ ‎∴ EF=‎6cm 7分 ‎ ‎2．（2008山东青岛）如图是一个用来盛爆米花的圆锥形纸杯，纸杯开口圆的直径EF长为‎10cm．母线OE(OF)长为‎10cm．在母线OF上的点A处有一块爆米花残渣，且FA＝2cm，一只蚂蚁从杯口的点E处沿圆锥表面爬行到A点．则此蚂蚁爬行的最短距离为 cm．‎ Ａ Ｆ Ｅ Ｏ 第14题图 ‎【参考答案】‎ ‎【解析】将圆锥侧面沿母线OF展开可得下图：‎ 则∠EOF＝5π÷（2π×10）×360°＝90°，在Rt△AOE中，OA＝8cm，OE＝10cm，根据勾股定理可得：AE＝cm，所以蚂蚁爬行的最短距离为cm.‎ 要计算蚂蚁在一个圆锥侧面的最短距离，我们一般是先将圆锥侧面展开，利用“两点之间，线段最短”来找出最短的路线，然后根据勾股定理，在一个直角三角形中求出这个最短的距离.‎ ‎14．(2008芜湖)如果圆锥的底面半径为3cm，母线长为6cm，那么它的侧面积等于　　．‎ 答案18π ‎13．(2008安徽)如图，在中，，，则劣弧的长为 cm．‎ 答案 第13题图 A B O ‎(2008江苏省无锡) 已知：如图，边长为的正内有一边长为的内接正 ‎（第12题）‎ ‎，则的内切圆半径为 ．‎ 答案：‎ A B 第12题图 ‎（2008江苏省宿迁）用圆心角为，半径为 的扇形做成一个无底的圆锥侧面，则此圆锥的底面半径为．‎ 答案：2‎ ‎（2008青海）12．如图，有一圆柱体，它的高为‎20cm，底面半径为‎7cm．在圆柱的下底面点处有一个蜘蛛，它想吃到上底面上与点相对的点处的苍蝇，需要爬行的最短路径是 cm（结果用带根号和的式子表示）．‎ 答案：‎ ‎（2008年江苏省南通市，27T，10分）27．在一次数学探究型学习活动中，某学习小组要制作一个圆锥体模型，操作规则是：在一块边长为16cm的正方形制片上剪出一个扇形和一个圆，使得扇形围成圆锥的侧面时，圆恰好是该圆锥的底面.它们首先设计了如图所示的方案一，发现这种方案不可行，于是他们调整了扇形和圆的半径，设计了如图所示的方案二.（两个方案的图中，圆与正方形相邻两边及扇形的弧均相切.方案一中扇形的弧与正方形的两边相切）‎ ‎（1）请说明方案一不可行的理由；‎ ‎（2）判断方案二是否可行？若可行，请确定圆锥的母线长及其底面圆半径；若不可行，请说明理由.‎ ‎ 方案一 方案二 ‎27.解：（1）理由如下：‎ ‎∵扇形的弧长＝16×＝8π，圆锥底面周长＝2πr，∴圆的半径为4cm.‎ 由于所给正方形纸片的对角线长为16cm，而制作这样的圆锥实际需要正方形直劈昂的对角线长为16＋4＋4＝（20＋4）cm，20＋4＞16，‎ ‎∴方案一不可行.‎ ‎（2）方案二可行.求解过程如下：‎ 设圆锥底面圆的半径为rcm，圆锥的母线长为Rcm，则 ‎，① 2πr＝.②‎ 由①②可得，r＝.‎ 故所求圆锥的母线长为cm，底面圆的半径为cm.‎ ‎（第15题图）‎ S B A ‎45cm ‎15．（08连云港）如图，扇形彩色纸的半径为‎45cm，圆心角为 ‎，用它制作一个圆锥形火炬模型的侧面（接头忽略不计），则这个圆锥的高约为 44.7 cm．（结果精确到‎0.1cm．参考数据：，，，）‎ ‎（2008徐州）如图,AB是⊙O的直径，点C在AB的延长线上，CD与⊙O相切于点D.若，若∠C＝18°，则∠CDA＝___126°___.‎ A B C E D O ‎（2008苏州）如图，为⊙O的直径，交⊙O于点，交⊙O于点，，．现给出以下四个结论：‎ ‎①；②；③；④．‎ 其中正确结论的序号是（ C ）‎ A．①② B．②③ C．②④ D．③④‎ ‎（2008 沈阳市）21．如图所示，是的一条弦，，垂足为，交于点，点在上．‎ E B D C A O 第21题图 ‎（1）若，求的度数；‎ ‎（2）若，，求的长．‎ 答案：解：（1）， 3分 ‎ 5分 ‎（2），，为直角三角形，‎ ‎，，‎ 由勾股定理可得 8分 ‎ 10分 ‎（2008 大连市）19．如图9，PA、PB是⊙O的切线，点A、B为切点，AC是⊙O的直径，∠ACB = 70°．求∠P的度数．‎ 答案：．解：连结OB………………………………………………1分 ‎∴∠AOB=2∠ACB………………………………………………3分 ‎∵∠ACB=70°,∴∠AOB=140°………………………………………………4分 ‎∵PA、PB分别是⊙O的切线，………………………………………………5分 ‎∴PA⊥OA，PB⊥OB………………………………………………7分 即∠PAO=∠PBO=90°‎ ‎∵四边形AOBP的内角和为360°………………………………………………8分 ‎∴∠P=360°－(90°+90°+140°) ………………………………………………9分 ‎=40°．………………………………………………10分 ‎6．(08荆门)如图3，将圆沿AB折叠后，圆弧恰好经过圆心，则等于( )C ‎(A)60°． (B)90°． (C)120°． (D)150°．‎ 图3‎ 图18‎ ‎26．(08荆门) (10分)如图18，⊙O是Rt△ABC的外接圆，AB为直径，∠ABC=30°，CD是⊙O的切线，ED⊥AB于F．‎ ‎(1)判断△CDE的形状；‎ ‎(2)设⊙O的半径为1且OF=，求证：△DCE≌△OCB．‎ 解：(1)∵∠ABC=30°，∴∠BAC=60°．‎ 又∵OA=OC， ∴△AOC是正三角形．‎ 又∵CD是切线，∴∠OCD=90°，‎ ‎∴∠DCE=180°－60°－90°=30°．‎ 而ED⊥AB于F，∴∠CED=90°－∠BAC=30°．‎ 故△CDE为等腰三角形． …………………………………………………4分 ‎(2)证明：在△ABC中，∵AB=2，AC=AO=1，∴BC==．‎ OF=，∴AF=AO＋OF=．‎ 又∵∠AEF=30°，∴AE=2AF=＋1． ∴CE=AE－AC==BC．‎ 而∠OCB=∠ACB－∠ACO=90°－60°=30°=∠ABC，‎ 故△CDE≌△COB． ……………………………………………10分 ‎4．(08泰州)如图，已知以直角梯形的腰为直径的半圆与梯形上底、下底以及腰均相切，切点分别是．若半圆的半径为2，梯形的腰为5，则该梯形的周长是（ ） D A． B．10 C．12 D．14‎ A D C O B E 第4题图 ‎1、(10T)(湖北省襄樊,3分)如图5，扇形纸扇完全打开后，外侧两竹条夹角为，的长为，贴纸部分的长为，则贴纸部分的面积为（ D ）‎ A． B．‎ C． D．‎ ‎2、（4T）（2008湖北省黄冈市，3分）已知圆锥的底面直径为4cm，其母线长为3cm，‎ 则它的侧面积为 ．‎ 15．（2008内江市）如图，是由绕点顺时针旋转而得，且点在同一条直线上，在中，若，，，则斜边旋转到所扫过的扇形面积为 ．‎C B A ‎（15题图）‎ 答案：‎ O C D B F A H E 7．（2008内江市）（10分）如图，内接于，，点是的中点．边上的高相交于点．‎ 试证明：‎ ‎（1）；‎ ‎（2）四边形是菱形．‎ 证明：（1）连结．‎ 点是的中点，‎ ‎， 1分 ‎，， 2分 ‎，‎ ‎ 3分 ‎ 5分 ‎（2）过点作于， 6分 ‎，， 7分 在与中，‎ ‎，，，‎ ‎ 8分 ‎．‎ ‎， 9分 四边形为菱形． 10分 ‎8．（2008资阳市）已知矩形ABCD的边AB＝15，BC＝20，以点B为圆心作圆，使A、C、D三点至少有一点在⊙B内，且至少有一点在⊙B外，则⊙B的半径r的取值范围是 ‎ A．r＞15 B．15＜r＜‎20 ‎ C．15＜r＜25 D．20＜r＜25‎ 答案：C 1. ‎（2008黄石）如图，在中，，，点为中点，将绕点按逆时针方向旋转得到，则点在旋转过程中所经过的路程为 ．（结果保留）‎ B A C D 答案：‎ ‎（济宁市二○○八）10．如图，小红要制作一个高为‎8cm，底面圆直径是‎12cm的圆锥形小漏斗，若不计接缝，不计损耗，则她所需纸板的面积是（ ）‎ A． B． C． D．‎ 答案：A ‎（济宁市二○○八）24．（9分）‎ 如图，内接于，过点的直线交于点，交的延长线于点，．‎ ‎（1）求证：；‎ ‎（2）如果，的半径为1，且为的中点，求的长．‎ 答案：（1）证明：连接． 1分 ‎，．‎ 又，‎ ‎． 3分 ‎，，‎ ‎．‎ ‎． 4分 ‎（2）解：由（1）知．‎ ‎，为等边三角形．‎ ‎． 5分 为的中点，．‎ ‎．‎ 为直径．． 7分 ‎．．‎ ‎，‎ ‎． 9分 ‎（2008深圳）1、如图8，点D是⊙O的直径CA延长线上一点，点B在⊙O上，且AB＝AD＝AO．‎ ‎（1）求证：BD是⊙O的切线．‎ ‎（2）若点E是劣弧BC上一点，AE与BC相交于点F，‎ 且△BEF的面积为8，cos∠BFA＝，求△ACF的面积．‎ 答案: （1）证明：连接BO， ‎ 方法一：∵ AB＝AD＝AO ‎∴△ODB是直角三角形 ‎ ‎∴∠OBD＝90° 即：BD⊥BO ‎ ∴BD是⊙O的切线． ‎ 方法二：∵AB＝AD， ∴∠D＝∠ABD ‎∵AB＝AO， ∴∠ABO＝∠AOB 又∵在△OBD中，∠D+∠DOB+∠ABO+∠ABD＝180°‎ ‎ ∴∠OBD＝90° 即：BD⊥BO ‎ ∴BD是⊙O的切线 ‎ ‎（2）解：∵∠C＝∠E，∠CAF＝∠EBF ‎∴△ACF∽△BEF ‎ ‎ ∵AC是⊙O的直径 ‎ ∴∠ABC＝90°‎ 在Rt△BFA中，cos∠BFA＝‎ ‎∴ ‎ ‎ 又∵＝8‎ ‎ ∴＝18 ‎ ‎（2008广州）2、如图10，扇形OAB的半径OA=3，圆心角∠AOB=90°，点C是上异于A、B的动点，过点C作CD⊥OA于点D，作CE⊥OB于点E，连结DE，点G、H在线段DE上，且DG=GH=HE ‎（1）求证：四边形OGCH是平行四边形 ‎（2）当点C在上运动时，在CD、CG、DG中，‎ 是否存在长度不变的线段？若存在，请求出该线段 的长度 ‎（3）求证：是定值 图10‎ 答案：（1）连结OC交DE于M，由矩形得OM＝CG，EM＝DM ‎　　　　因为DG=HE所以EM－EH＝DM－DG得HM＝DG ‎（2）DG不变，在矩形ODCE中，DE＝OC＝3，所以DG＝1‎ ‎（3）设CD＝x,则CE＝，由得CG＝‎ ‎　　所以所以HG＝3－1－‎ ‎ 所以3CH2＝‎ 所以 ‎（2008年贵阳市）24．（本题满分10分）‎ 如图10，已知是的直径，点在上，且，．‎ ‎（图10）‎ A B C D O ‎（1）求的值．（3分）‎ ‎（2）如果，垂足为，求的长．（3分）‎ ‎（3）求图中阴影部分的面积（精确到0.1）．（4分）‎ ‎（1）AB是⊙O的直径，点C在⊙O上 ‎∠ACB = 90o 1分 AB＝13，BC＝5‎ ‎． 3分 ‎（2）在Rt△ABC中，‎ ‎． 1分 ‎，‎ ‎． 3分 ‎（3）（平方单位）‎ ‎(2008 河南)10.如图所示，AB为⊙0的直径，AC为弦，OD∥BC交AC于点D，若AB=20cm,,则AD= cm 答案：5‎ ‎(2008 河南)22、（本题满分10分）‎ 如图，△ABC内接于⊙O，过点B作⊙O的切线，交于CA的延长线于点E，∠EBC=2∠C.‎ ‎(1)求证：AB=AC；(2)当=时，①求tan∠ABE的值；②如果AE=，求AC的值。‎ 答案：（本小题满分10分）‎ ‎（1）证明：∵BE切⊙O于点B，‎ ‎∴∠ABE＝∠C。························1分 ‎∵∠EBC＝2∠C，‎ 即 ∠ABE＋∠ABC＝2∠C。‎ ‎∴∠ABC＝∠C。‎ ‎∴AB＝AC。····························2分 ‎（2）解①如图，连接AO，交BC于点F。‎ ‎∵AB＝AC∴‎ ‎∴AO⊥BC，且BF＝FC。·······················3分 ‎∵ ∴∴…………………….….…….4分 设,，‎ 由勾股定理，得AF==………………5分 ‎∴……………………………6分 ‎②在EBA和ECB中， ‎ ‎∵∠E=∠E, ∠EBA=∠ECB, ∴△EBA∽△ECB,‎ ‎∴= ……………………………7分 ‎∵= ‎ ‎∴(※)…………………8分 由切割线定理，得 将(※)式代入上式，得…………………………9分 ‎∵,‎ ‎∴………………………………………………10分 O B AB 第4题图 ‎5cm (2008 鸡西)4．如图，小明想用图中所示的扇形纸片围成一个圆锥，‎ 已知扇形的半径为5cm，弧长是cm，那么围成的圆锥的高度 是 cm．‎ 答案：4‎ ‎16．已知圆锥的底面半径为‎2cm，母线长为‎4cm，则圆锥的侧面积为 cm2‎ 答案：‎ ‎18．如图，是的直径，是的弦，连接，‎ C B D O A 若，则的度数为 ．‎ 答案：55°‎ ‎（5题图）‎ O A B ‎（2008年遵义市）5．如图，是的弦，半径，，则弦的长为（ D ）‎ A． B． C．4 D．‎ ‎6．（2008·上海）如图1，从圆外一点引圆的两条切线，切点分别为．如果，，那么弦的长是（ ）‎ A．4 B．‎8 ‎ C． D．‎ 答案：B ‎14、（2008·重庆）在平面内，⊙O的半径为‎5cm，点P到圆心O的距离为‎3cm，则点P与⊙O的位置关系是 .‎ 答案：点在内 AB=sin∠DEC ===（2008肇庆市）24.如图6，在Rt△ABC中，∠ABC=90°，D是AC的中点，‎ ‎⊙O经过A、B、D三点，CB的延长线交⊙O于点E.‎ (1) 求证AE=CE； ‎ (2) EF与⊙O相切于点E，交AC的延长线于点F，‎ 若CD=CF=‎2cm，求⊙O的直径；‎ ‎ （3）若 （n>0），求sin∠CAB. ‎ 答案：证明：（1）连接DE，‎ ‎∵∠ABC=90°∴∠ABE=90°，‎ ‎∴AE是⊙O直径．‎ ‎∴∠ADE=90°，∴DE⊥AC．‎ 又∵D是AC的中点，∴DE是AC的垂直平分线．‎ ‎∴AE=CE． ‎ ‎（2）在△ADE和△EFA中，‎ ‎∵∠ADE=∠AEF=90°，∠DAE=∠FAE，‎ ‎∴△ADE∽△EFA．‎ ‎∴，‎ ‎∴． ‎ ‎∴AE=‎2‎cm． ‎ ‎∵AE是⊙O直径，EF是⊙O的切线，‎ ‎∴∠ADE=∠AEF=90°，∴Rt△ADE∽Rt△EDF．　　‎ ‎　∴．∵，AD=CD，‎ ‎∴CF=nCD，∴DF=（1+n）CD， ∴DE=CD．‎ 在Rt△CDE中，CE=CD+DE=CD+（CD） =（n+2）CD．‎ ‎∴CE=CD． ‎ ‎∵∠CAB=∠DEC，∴sin∠C ‎2008肇庆市）24.如图6，在Rt△ABC中，∠ABC=90°，D是AC的中点，‎ ‎⊙O经过A、B、D三点，CB的延长线交⊙O于点E.‎ (1) 求证AE=CE； ‎ (2) EF与⊙O相切于点E，交AC的延长线于点F，‎ 若CD=CF=‎2cm，求⊙O的直径；‎ ‎ （3）若 （n>0），求sin∠CAB. ‎ 答案：证明：（1）连接DE，‎ ‎∵∠ABC=90°∴∠ABE=90°，‎ ‎∴AE是⊙O直径．‎ ‎∴∠ADE=90°，∴DE⊥AC．‎ 又∵D是AC的中点，∴DE是AC的垂直平分线．‎ ‎∴AE=CE． ‎ ‎（2）在△ADE和△EFA中，‎ ‎∵∠ADE=∠AEF=90°，∠DAE=∠FAE，‎ ‎∴△ADE∽△EFA．‎ ‎∴，‎ ‎∴． ‎ ‎∴AE=‎2‎cm． ‎ ‎∵AE是⊙O直径，EF是⊙O的切线，‎ ‎∴∠ADE=∠AEF=90°，∴Rt△ADE∽Rt△EDF．　　‎ ‎　∴．∵，AD=CD，‎ ‎∴CF=nCD，∴DF=（1+n）CD， ∴DE=CD．‎ 在Rt△CDE中，CE=CD+DE=CD+（CD） =（n+2）CD．‎ ‎∴CE=CD． ‎ ‎∵∠CAB=∠DEC，∴sin∠CAB=sin∠DEC ==‎ ‎(2008湖北宜昌14．)如图，奥运五环旗上的五个环可以近似地看成五个圆，这五个圆反映 出的圆与圆的位置关系有 或者 ．‎ 答案：相交；外离 ‎（2008湖北武汉7）.如图是一个五环图案，它由五个圆组成，下排的两个圆的位置关系是 （　　）．‎ Ａ.内含　　　　Ｂ．外切　　　Ｃ．相交　　　　　Ｄ．外离 答案：D ‎（2008湖北武汉22）．（本题8分）如图，AB是⊙O的直径，AC是弦，∠BAC的平分线AD交⊙O于点D，DE⊥AC，交AC的延长线于点E，OE交AD于点F．⑴求证：DE是⊙O的切线；⑵若，求的值。‎ F E D C B A O 解：连接OD ‎ OA=OD DAO=ADO AD平分BAC CAD=DAO CAD=ADO AC∥OD DE⊥OD，‎ ‎⑵‎ 证明：连接BC交OD与点M 由（1）知，OM∥AC.OM=AC 设AC=3k,AB=5k 则BC=4k 所以OM=AC=1.5k,，MD=OD-OM=2.5k-1.5k=k 易证，四边形CEDM为矩形，故CE=MD=k,则AE=3k+k=4k ‎(第12题)‎ ‎===‎ ‎23.圆中的计算 ‎(2008湖北宜昌12.)翔宇学中的铅球场如图所示，已知扇形AOB的面积是‎36米2，‎ 的长度为‎9米，那么半径OA＝ 米．‎ 答案：8‎ ‎(2008湖北宜昌21)．如图，⊙O的半径OD经过弦AB(不是直径)的中点C，过AB的延长线上一点P作⊙O的切线PE，E为切点，PE∥OD；延长直径AG交PE于点H；直线DG交OE于点F，交PE于点K．‎ ‎(第21题)‎ ‎（1）求证：四边形OCPE是矩形；‎ ‎（2）求证：HK＝HG；‎ ‎（3）若EF＝2，FO＝1，求KE的长．‎ 解：(1)∵AC＝BC，AB不是直径，‎ ‎∴OD⊥AB，∠PCO＝90°(1分)‎ ‎∵PE∥OD,∴∠P＝90°，‎ ‎∵PE是切线，∴∠PEO＝90°，(2分)‎ ‎∴四边形OCPE是矩形.(3分)‎ ‎(2)∵OG＝OD,∴∠OGD＝∠ODG.‎ ‎∵PE∥OD,∴∠K＝∠ODG.(4分)‎ ‎∵∠OGD＝∠HGK,∴∠K＝∠HGK,‎ ‎∴HK＝HG.(5分)‎ ‎(3)∵EF＝2，OF＝1,∴EO＝DO＝3.(6分)‎ ‎∵PE∥OD，∴∠KEO＝∠DOE，∠K＝∠ODG.‎ ‎∴△OFD∽△EFK，(7分)∴EF∶OF＝KE∶OD＝2∶1,‎ ‎∴KE＝6.(8分)‎ ‎∵∠OGD＝∠HGK,∴∠K＝∠HGK,‎ ‎∴HK＝HG.(5分)‎ ‎(3)∵EF＝2，OF＝1,∴EO＝DO＝3.(6分)‎ ‎∵PE∥OD，∴∠KEO＝∠DOE，∠K＝∠ODG.‎ ‎∴△OFD∽△EFK，(7分)∴EF∶OF＝KE∶OD＝2∶1,‎ ‎∴KE＝6.(8分)‎ ‎18．（2008·上海）在中，，（如图6）．如果圆的半径为，且经过点，那么线段的长等于 ．‎ 答案：3或5‎