中考九年级数学学练测102相似图形的应用

中考九年级数学学练测102相似图形的应用

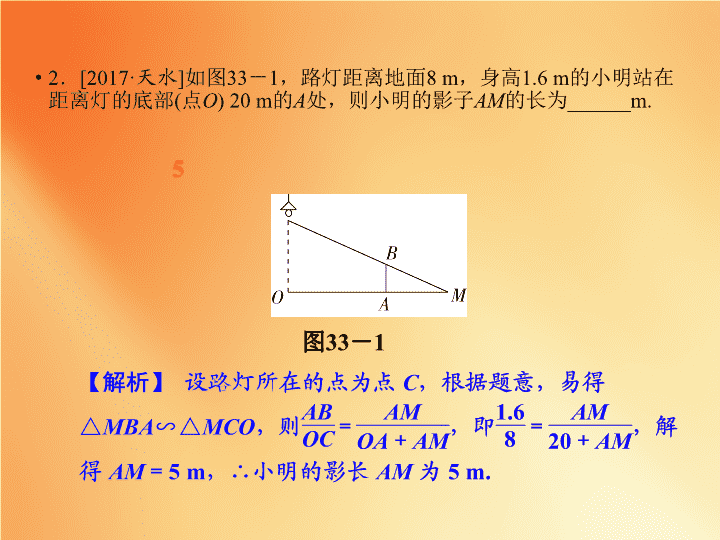
相似图形的应用 1 ．丽水市第一座横跨瓯江的单塔斜拉式大桥紫金大桥在比例尺为 1∶500 的图纸上的长度约为 1.04 m ，则大桥的实际长度约是 ( 　 　 ) A ． 104 m B ． 1 040 m C ． 5 200 m D ． 520 m 【 解析 】 设大桥的实际长度为 x ，依题意，得 1∶500 ＝ 1.04∶ x ，解得 x ＝ 1.04×500 ＝ 520(m) ． 小题热身 D 2 ． [2017· 天水 ] 如图 33 － 1 ，路灯距离地面 8 m ，身高 1.6 m 的小明站在距离灯的底部 ( 点 O ) 20 m 的 A 处，则小明的影子 AM 的长为 ______m. 图 33 － 1 5 3 ．如图 33 － 2 ，已知零件的外径为 25 mm ，现用一个交叉卡钳 ( 两条尺长 AC 和 BD 相等， OC ＝ OD ) 量零件的内孔直径 AB . 若 OC ∶ OA ＝ 1∶2 ，量得 CD ＝ 10 mm ，则零件的厚度 x ＝ _______mm. 图 33 － 2 2.5 4 ．如图 33 － 3 ，阳光通过窗口照射到室内 ( 太阳光线是平行光线 ) ，在地面上留下 2.7 m 宽的亮区，已知亮区到窗口下墙脚的距离 EC ＝ 8.7 m ，窗口高 AB ＝ 1.8 m ，求窗口底边离地面的高 BC . 图 33 － 3 一、必知 2 知识点 1 ． 相似三角形的应用 与相似三角形有关的实际应用： (1) 利用投影、平行线、标杆等构造相似三角形； (2) 测量底部可以到达的物体高度； (3) 测量底部不可到达的物体高度； (4) 测量不可到达对岸的河宽． 几何图形的证明与计算：计算线段的数量关系，求线段的长度和图形的面积大小等．解法是先根据已知条件构造相似三角形，再利用相似三角形性质求解． 考点管理 2 ． 位似图形 位似图形：如果两个图形满足以下两个条件：所有经过对应点所在的直线都相交于同一 ______ ；这个交点到两个对应点的距离之比都相等，那么这两个图形叫做位似图形，经过各对应两点的直线的交点叫做 ___________ ，位似中心到两个对应点的距离之比叫做 _________ ． 坐标系中的位似变换：当以坐标原点为位似中心时，若原图形上点的坐标为 ( x ， y ) ，位似图形与原图形的位似比为 k ，则位似图形上的对应点的坐标为 ( kx ， ky ) 或 ( － kx ，－ ky ) ． 点 位似中心 位似比 二、必会 2 方法 1 ．相似三角形的应用技巧 相似三角形的知识在实际生产和生活中有着广泛的应用，这一应用是建立在数学建模和数形结合思想的基础上，把实际问题转化为数学问题，通过求解数学问题达到解决实际问题的目的． 2 ．位似图形的识别 识别位似图形，关键是看两个相似多边形的对应顶点所在的直线是否相交于一点，相交于一点的就是位似图形，交点就是位似中心，否则就不是． 利用相似解决生活实际问题 [2016· 陕西 ] 某市为了打造森林城市，树立城市新地标，实现绿色、共享发展理念，在城南建起了 “ 望月阁 ” 及环阁公园．小亮、小芳等同学想用一些测量工具和所学的几何知识测量 “ 望月阁 ” 的高度，以此检验自己掌握知识和运用知识的能力．经过观察他们发现，观测点与 “ 望月阁 ” 底部间的距离不易测得，因此需要两次测量，于是他们首先用平面镜进行测量．方法如下：如图 33 － 4 ，小芳在小亮和 “ 望月阁 ” 之间的直线 BM 上平放一平面镜，在镜面上做了一个标记，这个 标记在直线 BM 上的对应位置为点 C ，镜子不动，小亮看着镜面上的标记来回走动，走到点 D 时，看到 “ 望月阁 ” 顶端点 A 在镜面中的像与镜面上的标记重合，这时，测得小亮眼睛与地面的高度 ED ＝ 1.5 m ，走过的距离 CD ＝ 2 m ．然后，在阳光下，他们用测影长的方法进行了第二次测量．方法如下：小亮从 D 点沿 DM 方向走了 16 m ，到达 “ 望月阁 ” 影子的末端 F 点处，此时，测得小亮身高 FG 的影长 FH ＝ 2.5 m ．已知 FG ＝ 1.65 m ， AB ⊥ BM ， ED ⊥ BM ， GF ⊥ BM ，其中，测量时所使用的平面镜的厚度忽略不计，请你根据题中提供的相关信息，求出“望月阁”的高 AB . 【 解析 】 根据镜面反射原理结合相似三角形的判定方法，得出 △ ABC ∽△ EDC ，△ ABF ∽△ GFH ，进而利用相似三角形的性质得出 AB 的长． 图 33 － 4 1 ．一天晚上，李明和张龙利用灯光下的影子长来测量一路灯 D 的高度．如图 33 － 5 ，当李明走到点 A 处时，张龙测得李明直立时身高 AM 与其影子长 AE 正好相等，接着李明沿 AC 方向继续向前走，走到点 B 处时，李明直立时身高 BN 的影子恰好是 图 33 － 5 线段 AB ，并测得 AB ＝ 1.25 m ，已知李明直立时的身高为 1.75 m ，求路灯的高 CD ( 结果精确到 0.1 m) ． 2 ． [2018· 中考预测 ] 如图 33 － 6 ，在一面与地面垂直的围墙的同侧有一根高 10 m 的旗杆 AB 和一根高度未知的电线杆 CD ，它们都与地面垂直，为了测得电线杆的高度，一个小组的同学进行了如下测量：某一时刻，在太阳光照射下，旗杆落在围墙上的影子 EF 的长度为 2 m ，落在地面上的影子 BF 的长为 10 m ，而电线杆落在围墙上的影子 GH 的长度为 3 m ，落在地面上的影子 DH 的长为 5 m ，依据这些数据，该小组的同学计算出了电线杆的高度． (1) 该小组的同学在这里利用的是 _______ 投影的有关知识进行计算的； (2) 试计算出电线杆的高度，并写出计算的过程． 图 33 － 6 平行 变式跟进 2 答图 相似三角形与其他知识的综合运用 [2016· 金华 ] 如图 33 － 7 ，在四边形 ABCD 中，∠ B ＝ 90° ， AC ＝ 4 ， AB ∥ CD ， DH 垂直平分 AC ， H 为垂足．设 AB ＝ x ， AD ＝ y ，则 y 关于 x 的函数关系用图象大致可以表示为 ( 　 　 ) 图 33 － 7 D 图 33 － 8 A 变式跟进 1 答图 2 ．如图 33 － 9 ，在矩形 ABCD 中， E 为 CD 的中点， F 为 BE 上的一点，连结 CF 并延长交 AB 于点 M ， MN ⊥ CM 交射线 AD 于点 N . (1) 当 F 为 BE 中点时，求证： AM ＝ CE ； 解 ： (1) 证明： ∵ F 为 BE 的中点， ∴ BF ＝ EF .∵ AB ∥ CD ， ∴∠ MBF ＝ ∠ CEF ，∠ BMF ＝ ∠ ECF . ∴△ BMF ≌△ ECF ( AAS ) ． ∴ MB ＝ CE . ∵ AB ＝ CD ， CE ＝ DE ， ∴ MB ＝ AM ，∴ AM ＝ CE ； 图 33 － 9 【 点悟 】 　此类问题一般涉及相似三角形的判定与性质、特殊四边形的性质以及锐角三角函数的定义等．常常用到数形结合思想、分类讨论思想等． 坐标系中的位似变换 ( 选学 ) [2017· 成都 ] 如图 33 － 10 ，四边形 ABCD 和 A ′ B ′ C ′ D ′ 是以点 O 为位似中心的位似图形，若 OA ∶ OA ′ ＝ 2∶3 ，则 四边形 ABCD 与四边形 A ′ B ′ C ′ D ′ 的面积比为 ( 　 　 ) 图 33 － 10 A 【 解析 】 由位似的性质，得四边形 ABCD 和 A ′ B ′ C ′ D ′ 的位似比为 2∶3 ，∴四边形 ABCD 与四边形 A ′ B ′ C ′ D ′ 的面积比为 4∶9. 【 点悟 】 　在平面直角坐标系中，如果位似变换是以原点为位似中心，相似比为 k ，那么位似图形对应点的坐标的比等于 k 或－ k ，解答此类问题时，一定要考虑两种情况． 1 ． [2017· 绥化 ] 如图 33 － 11 ，△ A ′ B ′ C ′ 是 △ ABC 以点 O 为位似中心经过位似变换得到的，若 △ A ′ B ′ C ′ 的面积与 △ ABC 的面积比是 4∶9 ，则 OB ′ ∶ OB 为 ( 　 　 ) A ． 2 ∶ 3 B ． 3 ∶ 2 C ． 4 ∶ 5 D ． 4 ∶ 9 图 33 － 11 A 图 33 － 12 图 33 － 1 3 图 33 － 14 (1 ， 2) 5 ． [2017· 滨州 ] 在平面直角坐标系中，点 C ， D 的坐标分别为 (2 ， 3) ， (1 ， 0) ．现以原点为位似中心，将线段 CD 放大得到线段 AB ，若点 D 的对应点 B 在 x 轴上，且 OB ＝ 2 ，则点 C 的对应点点 A 的坐标为 ____________________ ． 【 解析 】 由 “ 点 B 在 x 轴上且 OB ＝ 2” 可知 B (2 ， 0) 或 B ( － 2 ， 0) ，∴线段 CD 与线段 AB 的位似比为 1∶2 或 1∶( － 2) ，根据 “( x ， y ) 以原点为位似中心的对应点坐标为 ( kx ， ky )” 可知点 C 的对应点 A 的坐标为 (4 ， 6) 或 ( － 4 ，－ 6) ． (4 ， 6) 或 ( － 4 ，－ 6) 必明 3 易错点 1 ．位似图形是相似图形的一个特例，位似图形一定是相似图形，相似图形不一定是位似图形． 2 ．如果只说明两个三角形相似，而不是说 “ 相似于 ” ，则需要分类讨论． 3 ．已知一个图形和位似中心作位似图形时，要注意运用分类讨论思想，考虑两个图形在位似中心同侧或位似中心的两侧两种情况，避免出现漏解． 比例尺理解偏差 [ 淮安中考 ] 在比例尺为 1∶200 的地图上，测得 A ， B 两地间的图上距离为 4.5 cm ，则 A ， B 两地间的实地距离为 ________m. 【 错解 】 设 A ， B 两地间的实地距离为 x m ， ∴ 1 ∶ 200 ＝ 4.5∶ x ， ∴ x ＝ 900 m ， 即 A ， B 两地间的实地距离为 900 m. 【 错因 】 求两条线段的比例时单位要统一，解答本题时要设实际长度为 x cm ，结果的单位要化为 m ，否则容易出错． 【 正解 】 设 A ， B 两地间的实地距离为 x cm ， ∴ 1 ∶ 200 ＝ 4.5∶ x ， ∴ x ＝ 900 cm ， ∵ 900 cm ＝ 9 m ， ∴ A ， B 两地间的实地距离为 9 m. 对位似变换考虑不全 ( 选学 ) 图 33 － 15 A ． (3 ， 2) B ． ( － 2 ，－ 3) C ． (2 ， 3) 或 ( － 2 ，－ 3) D ． (3 ， 2) 或 ( － 3 ，－ 2) 【 错解 】A 【 正解 】D