30-2 第2课时 二次函数y=a(x-h)2和y=a(x-h)2+k的图像和性质 冀教版

30-2 第2课时 二次函数y=a(x-h)2和y=a(x-h)2+k的图像和性质 冀教版

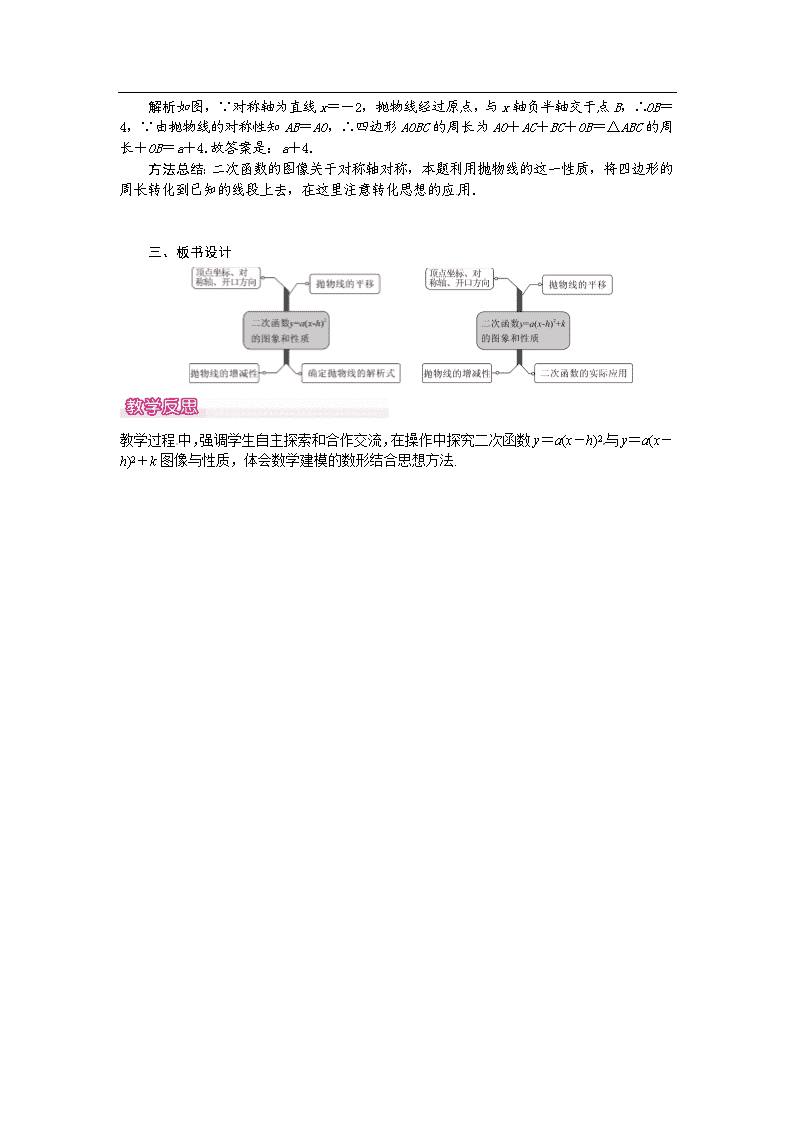
第2课时 二次函数y=a（x-h）2和y=a（x-h）2+k的图像和性质 ‎　　　　　　　　　　　　　　　　　　　‎ ‎1．会用描点法画出y＝a(x－h)2和y＝a(x－h)2＋k的图像．‎ ‎2．掌握形如y＝a(x－h)2和y＝a(x－h)2＋k二次函数图像的性质，并会应用．‎ ‎3．理解二次函数y＝a(x－h)2及y＝a(x－h)2＋k与y＝ax2之间的联系．‎ 一、情境导入 涵洞是指在公路工程建设中，为了使公路顺利通过水渠不妨碍交通，修筑于路面以下的排水孔道(过水通道)，通过这种结构可以让水从公路的下面流过．从如图所示的直角坐标系中，你能得到函数图像解析式吗？‎ 二、合作探究 探究点一：二次函数y＝a(x－h)2的图像和性质 ‎【类型一】y＝a(x－h)2的图像与性质的识别 ‎ 已知抛物线y＝a(x－h)2(a≠0)的顶点坐标是(－2，0)，且图像经过点(－4，2)，求a，h的值．‎ 解：∵抛物线y＝a(x－h)2(a≠0)的顶点坐标为(－2，0)，∴h＝－2.又∵抛物线y＝a(x＋2)2经过点(－4，2)，∴(－4＋2)2·a＝2，∴a＝.‎ 方法总结：抛物线y＝a(x－h)2的顶点坐标为(h，0)，对称轴是直线x＝h.‎ ‎【类型二】二次函数y＝a(x－h)2增减性的判断 ‎ 对于二次函数y＝9(x－1)2，下列结论正确的是(　　)‎ A．y随x的增大而增大 B．当x＞0时，y随x的增大而增大 C．当x＞－1时，y随x的增大而增大[来源:学科网]‎ D．当x＞1时，y随x的增大而增大 解析：由于a＝9＞0，抛物线开口向上，而h＝1，所以当x＞1时，y随x的增大而增大．故选D.‎ ‎【类型三】确定y＝a(x－h)2与y＝ax2的关系 ‎ 能否向左或向右平移函数y＝－x2的图像，使得到的新的图像过点(－9，－8)？若能，请求出平移的方向和距离；若不能，请说明理由．[来源:Z+xx+k.Com]‎ 解：能，设平移后的函数为y＝－(x－h)2，将x＝－9，y＝－8代入得－8＝－(－9－h)‎ ‎2，所以h＝－5或h＝－13，所以平移后的函数为y＝－(x＋5)2或y＝－(x＋13)2.即抛物线的顶点为(－5，0)或(－13，0)，所以向左平移5或13个单位．‎ 方法总结：根据抛物线平移的规律，向右平移h个单位后，a不变，括号内变“减去h”；若向左平移h个单位，括号内应“加上h”，即“左加右减”．‎ ‎【类型四】y＝a(x－h)2的图像与几何图形的综合 ‎ 把函数y＝x2的图像向右平移4个单位后，其顶点为C，并与直线y＝x分别相交于A、B两点(点A在点B的左边)，求△ABC的面积．‎ 解析：利用二次函数平移规律先确定平移后抛物线解析式，确定C点坐标，再解由得到的二次函数解析式与y＝x组成的方程组，确定A、B两点的坐标，最后求△ABC的面积．‎ 解：平移后的函数为y＝(x－4)2，顶点C的坐标为(4，0)，解方程组得或∵点A在点B的左边，∴A(2，2)，B(8，8)．∴S△ABC＝S△OBC－S△OAC＝OC×8－OC×2＝12.‎ 方法总结：两个函数交点的横纵坐标与两个解析式组成的方程组的解是一致的．‎ 探究点二：二次函数y＝a(x－h)2+k的图像和性质 ‎【类型一】利用平移确定y＝a(x－h)2＋k的解析式 ‎ 将抛物线y＝x2向右平移2个单位，再向下平移1个单位，所得的抛物线是(　　)‎ A．y＝(x－2)2－1 B．y＝(x－2)2＋1[来源:学|科|网Z|X|X|K][来源:学科网ZXXK]‎ C．y＝(x＋2)2＋1 D．y＝(x＋2)2－1‎ 解析：由“上加下减”的平移规律可知，将抛物线y＝x2向下平移1个单位所得抛物线的解析式为：y＝x2－1；由“左加右减”的平移规律可知，将抛物线y＝x2－1向右平移2个单位所得抛物线的解析式为y＝(x－2)2－1，故选A.‎ ‎【类型二】y＝a(x－h)2＋k的图像与几何图形的综合 ‎ 如图，在平面直角坐标系中，点A在第二象限，以A为顶点的抛物线经过原点，与x轴负半轴交于点B，对称轴为直线x＝－2，点C在抛物线上，且位于点A、B之间(C不与A、B重合)．若△ABC的周长为a，则四边形AOBC的周长为________．(用含a的式子表示)‎ 解析：如图，∵对称轴为直线x＝－2，抛物线经过原点，与x轴负半轴交于点B，∴OB＝4，∵由抛物线的对称性知AB＝AO，∴四边形AOBC的周长为AO＋AC＋BC＋OB＝△ABC的周长＋OB＝a＋4.故答案是：a＋4.‎ 方法总结：二次函数的图像关于对称轴对称，本题利用抛物线的这一性质，将四边形的周长转化到已知的线段上去，在这里注意转化思想的应用．‎ 三、板书设计 ‎ ‎ ‎[来源:学。科。网]‎ 教学过程中，强调学生自主探索和合作交流，在操作中探究二次函数y＝a(x－h)2与y＝a(x－h)2＋k图像与性质，体会数学建模的数形结合思想方法.‎