2009年湖南省常德市初中毕业学业考试数学试题

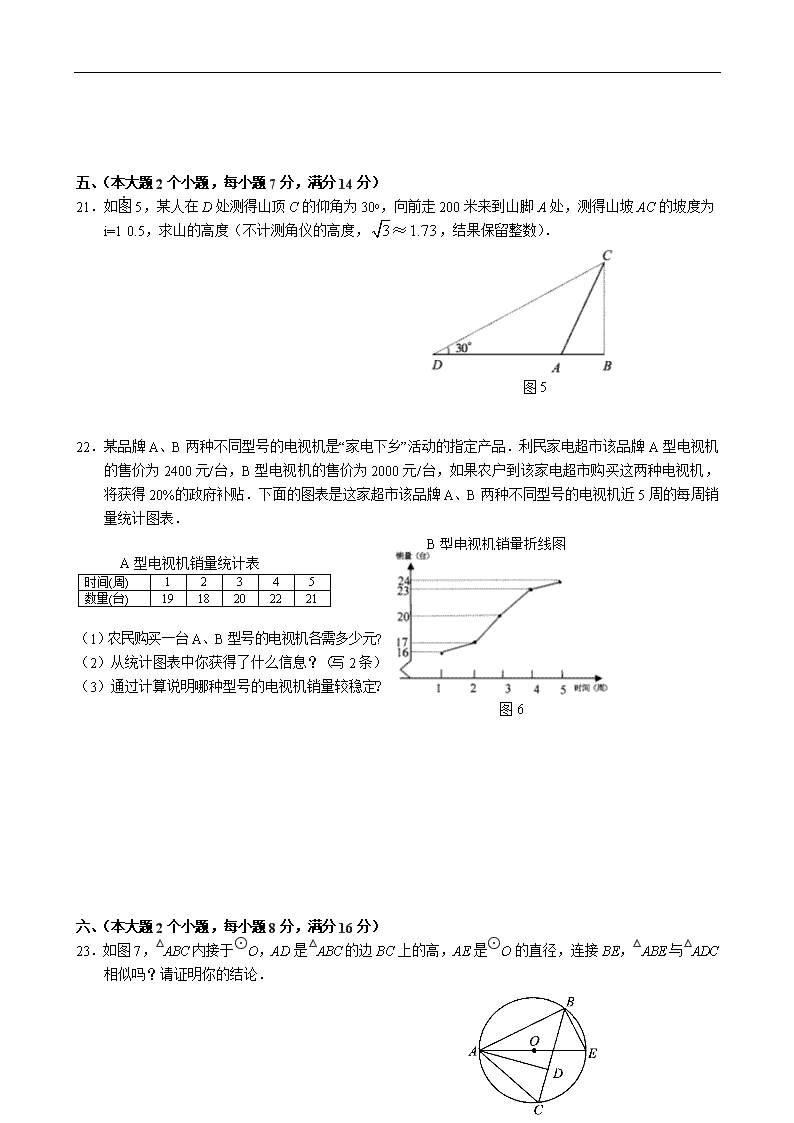
2009年湖南省常德市初中毕业学业考试数学试题

‎2009年常德市初中毕业学业考试 数学试题卷 ‎ ‎ 准考证号 姓 名_______________‎ ‎ ‎ 考生注意：1、请考生在试题卷首填写好准考证号及姓名．‎ ‎ 2、请将答案填写在答题卡上，填写在试题卷上的无效．‎ ‎ 3、本学科试题卷共 4页，七道大题，满分120 分，考试时量 120 分钟．‎ ‎ 4、考生可带科学计算器参加考试．‎ 一、填空题（本大题8个小题，每小题3分，满分24分）‎ ‎1．3的倒数等于 ．‎ ‎2．因式分解： ．‎ ‎3．已知△ABC中，BC=‎6cm，E、F分别是AB、AC的中点，那么EF长是 　　 cm．‎ 图1‎ ‎4．一个圆锥的母线长为‎5cm，底面圆半径为‎3 cm，则这个圆锥的侧面积是 cm2（结果保留）．‎ ‎5．如图1，已知点C为反比例函数上的一点，过点C向坐标轴引垂线，垂足分别为A、B，那么四边形AOBC的面积为 ．‎ ‎6．如图2，△ABC向右平移4个单位后得到△A′B′C′，则A′点的坐标是 　 ．‎ 图3‎ 图2‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎7．如图3，已知，∠1=130o，∠2=30o，则∠C= ．‎ ‎8．一个函数的图象关于轴成轴对称图形时，称该函数为偶函数． 那么在下列四个函数①；②；③；④中，偶函数是 　　 （填出所有偶函数的序号）．‎ 二、选择题（本大题8个小题，每小题3分，满分24分）‎ ‎9．的结果是（　　）‎ A． B． C． D． ‎ ‎10．要使分式有意义，则应满足的条件是（　　）‎ ‎ A． B． C． D．‎ ‎11．为了响应中央号召，今年我市加大财政支农力度，全市农业支出累计达到234 760 000元，其中234 760‎ ‎ 000元用科学记数法可表示为（　　）（保留三位有效数字）．‎ ‎ A．2.34×108元 B．2.35×108元 ‎ ‎ C．2.35×109 元 D．2.34×109元 ‎12．设，，，，则按由小到大的顺序排列正确的是（　　）‎ ‎ A． B． ‎ ‎ C． D．‎ ‎13．下面事件：①掷一枚硬币，着地时正面向上；②在标准大气压下，水加热到‎100℃‎会沸腾；③买一张福利彩票，开奖后会中奖；④明天会下雨．其中，必然事件有（　　）‎ ‎ A．1个 B．2个 C．3个 D．4个 ‎14．如图4，两个同心圆的半径分别为‎3cm和‎5cm，弦AB与小圆相切于点C，则AB的长为（　　）‎ 图4‎ A B O ‎·‎ C ‎ A．‎4cm B．‎‎5cm ‎ C．‎6cm D．‎‎8cm ‎15．下列命题中错误的是（　　）‎ A．两组对边分别相等的四边形是平行四边形 B．对角线相等的平行四边形是矩形 ‎ C．一组邻边相等的平行四边形是菱形 ‎ D．一组对边平行的四边形是梯形 ‎16．甲、乙、丙三人进行乒乓球比赛，规则是：两人比赛，另一人当裁判，输者将在下一局中担任裁判，每一局比赛没有平局．已知甲、乙各比赛了4局，丙当了3次裁判．问第2局的输者是（　　）‎ A． 甲 B． 乙 C． 丙 D．不能确定 三、（本大题2个小题，每小题5分，满分10分）‎ ‎17．解方程： 18．解不等式组: ‎ 四、（本大题2个小题，每小题6分，满分12分）‎ ‎19． 化简:‎ ‎20．“六一”儿童节期间，某儿童用品商店设置了如下促销活动：如果购买该店100元以上的商品，就能参加一次游戏，即在现场抛掷一个正方体两次（这个正方体相对的两个面上分别画有相同图案），如果两次都出现相同的图案，即可获得价值20元的礼品一份，否则没有奖励．求游戏中获得礼品的概率是多少？‎ 五、（本大题2个小题，每小题7分，满分14分）‎ ‎21．如图5，某人在D处测得山顶C的仰角为30o，向前走‎2‎‎00米来到山脚A处，测得山坡AC的坡度为i=1∶0.5，求山的高度（不计测角仪的高度，，结果保留整数）．‎ 图5‎ ‎22．某品牌A、B两种不同型号的电视机是“家电下乡”活动的指定产品．利民家电超市该品牌A型电视机的售价为2400元/台，B型电视机的售价为2000元/台，如果农户到该家电超市购买这两种电视机，将获得20%的政府补贴．下面的图表是这家超市该品牌A、B两种不同型号的电视机近5周的每周销量统计图表．‎ B型电视机销量折线图 图6‎ A型电视机销量统计表 时间(周)‎ ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ 数量(台)‎ ‎19‎ ‎18‎ ‎20‎ ‎22‎ ‎21‎ ‎（1）农民购买一台A、B型号的电视机各需多少元?‎ ‎（2）从统计图表中你获得了什么信息？（写2条）‎ ‎（3）通过计算说明哪种型号的电视机销量较稳定?‎ 六、（本大题2个小题，每小题8分，满分16分）‎ ‎23．如图7，△ABC内接于⊙O，AD是△ABC的边BC上的高，AE是⊙O的直径，连接BE，△ABE与△ADC相似吗？请证明你的结论．‎ 图7‎ ‎24．常德市工业走廊南起汉寿县太子庙镇，北至桃源县盘塘镇创元工业园．在这一走廊内的工业企业2008年完成工业总产值440亿元，如果要在2010年达到743.6亿元，那么2008年到2010年的工业总产值年平均增长率是多少？《常德工业走廊建设发展规划纲要（草案）》确定2012年走廊内工业总产值要达到1200亿元，若继续保持上面的增长率，该目标是否可以完成？‎ 七、（本大题2个小题，每小题10分，满分20分）‎ ‎25．已知二次函数过点A （0，），B（，0），C（）．‎ ‎ （1）求此二次函数的解析式；‎ ‎ （2）判断点M（1，）是否在直线AC上？‎ 图8‎ ‎ （3）过点M（1，）作一条直线与二次函数的图象交于E、F两点（不同于A，B，C三点），请自已给出E点的坐标，并证明△BEF是直角三角形．‎ ‎26．如图9，若△ABC和△ADE为等边三角形，M，N分别EB，CD的中点，易证：CD=BE，△AMN是等边三角形．‎ ‎ （1）当把△ADE绕A点旋转到图10的位置时，CD=BE是否仍然成立？若成立请证明，若不成立请说明理由；（4分）‎ ‎ （2）当△ADE绕A点旋转到图11的位置时，△AMN是否还是等边三角形？若是，请给出证明，并求出当AB=2AD时，△ADE与△ABC及△AMN的面积之比；若不是，请说明理由．（6分）‎ 图9 图10 图11‎ 图8‎ ‎2009年常德市初中毕业学业考试 数学参考答案及评分细则 ‎ 说明:‎ ‎ （一）《答案》中各行右端所注分数表示正确作完该步应得的累加分数，全卷满分120分．‎ ‎ （二）《答案》中的解法只是该题解法中的一种或几种，如果考生的解法和本《答案》不同，可参照本答案中的标准给分．‎ ‎ （三）评卷时要坚持每题评阅到底，勿因考生解答中出现错误而中断本题的评阅．如果考生的解答在某一步出现错误，影响后继部分而末改变本题的内容和难度者，视影响程度决定后面部分的得分，但原则上不超过后面部分应得分数的一半，如有严重的概念错误，就不给分．‎ 一、填空题（本大题8个小题，每小题3分，满分24分）‎ ‎1． 2． 3．3 4．15‎ ‎5． 6 6．（1，2） 7． 20o 8．④ ‎ 二、选择题（本大题8个小题，每小题3分，满分24分）‎ ‎9．C 10．B 11． B 12．A 13． A 14． D 15．D 16．C ‎ 三、（本大题2个小题，每小题5分，满分10分）‎ ‎17．原方程变形得 2分 ‎∴ 4分 经检验是原方程的根 5分 ‎18．解不等式（1）得 2分 ‎ 解不等式（2）得 4分 原不等式组的解集为 5分 四、（本大题2个小题，每小题6分，满分12分）‎ ‎19． 原式= 2分 ‎ = 4分 ‎ = 6分 说明：通分；作差并整理；约分各2分．‎ ‎20．解法一：设这三种图案分别用A、B、C表示，则列表得 第一次 第二次 A B C A ‎（A，A）‎ ‎（A，B）‎ ‎（A，C）‎ B ‎（B，A）‎ ‎（B，B）‎ ‎（B，C）‎ C ‎（C，A）‎ ‎（C，B）‎ ‎（C，C）‎ ‎ 4分 ‎∴ 6分 解法二：正确列出树状图 （略） 4分 ‎∴ 6分 五、（本大题2个小题，每小题7分，满分14分）‎ ‎21． 设山高BC =，则AB=， 2分 由，得 4分 ‎， 5分 解得米 7分 ‎22．（1）2400×（1-20%）=1920（元），2000×（1-20%）=1600（元） 2分 所以农民购买一台A型电视机需1920元，购买一台B型电视机需1600元．‎ ‎ （2）答案不唯一．‎ 如：B型电视机的销量呈逐渐增长趋势；A、B两种型号的电视机的销量较为接近，‎ 且第3周的销量相同；B型第2周的销量为17台等等． 4分 ‎（3），‎ 由计算器计算得：， ∵，‎ ‎∴A型号的电视机销量较稳定． 7分 注：（3）中没有计算直接下结论的给1分．‎ 六、（本大题2个小题，每小题8分，满分16分）‎ ‎23．△ABE 与△ADC相似．理由如下：‎ 在△ABE与△ADC中 ‎∵AE是⊙O的直径， ∴∠ABE=90o， 2分 ‎∵AD是△ABC的边BC上的高，‎ ‎∴∠ADC=90o， ∴∠ABE=∠ADC． 4分 又∵同弧所对的圆周角相等， ∴∠BEA=∠DCA． 6分 ‎∴△ABE ～△ADC． 8分 ‎24．设2008年到2010年的年平均增长率为 x ，则 3分 ‎ 化简得 ： ， （舍去） 6分 ‎ 8分 答：2008年到2010年的工业总产值年平均增长率为 30%，若继续保持上面的增长率，‎ 在2012年将达到1200亿元的目标．‎ 七、（本大题2个小题，每小题10分，满分20分）‎ 图8‎ ‎25．（1）设二次函数的解析式为（）， ‎ 把A （0，），B（，0），C（）代入得 解得 a=2 ， b=0 ， c=－2，‎ ‎∴ 3分 ‎（2）设直线AC的解析式为 ，‎ 把A （0，－2），C（）代入得 ‎， 解得 ，∴‎ 当x=1时， ∴M（1，）在直线AC上 5分 ‎（3）设E点坐标为（），则直线EM的解析式为 由 化简得，即，‎ ‎ ∴F点的坐标为（）． 6分 过E点作EH⊥x轴于H，则H的坐标为（）．‎ ‎∴ ∴，‎ 类似地可得 ，‎ ‎， 9分 ‎ ∴，∴△BEF是直角三角形． 10分 图10‎ C N D A M E B ‎26．解：（1）CD=BE．理由如下:　 1分 ‎ ∵△ABC和△ADE为等边三角形 ‎ ‎∴AB=AC，AE=AD，∠BAC=∠EAD=60o ‎ ∵∠BAE =∠BAC－∠EAC =60o－∠EAC，‎ ‎∠DAC =∠DAE－∠EAC =60o－∠EAC， ‎ ‎∴∠BAE=∠DAC， ∴△ABE ≌ △ACD 3分 ‎ ∴CD=BE 4分 ‎ （2）△AMN是等边三角形．理由如下： 5分 图11‎ C N D A B M E ‎ ∵△ABE ≌ △ACD， ∴∠ABE=∠ACD．‎ ‎ ∵M、N分别是BE、CD的中点，‎ ‎ ∴BM=‎ ‎ ∵AB=AC，∠ABE=∠ACD， ∴△ABM ≌ △ACN．‎ ‎ ∴AM=AN，∠MAB=∠NAC． 6分 ‎ ∴∠NAM=∠NAC+∠CAM=∠MAB+∠CAM=∠BAC=60o ‎ ∴△AMN是等边三角形． 7分 ‎ 设AD=a，则AB=‎2a．‎ ‎ ∵AD=AE=DE，AB=AC， ∴CE=DE．‎ ‎ ∵△ADE为等边三角形， ∴∠DEC=120 o， ∠ADE=60o，‎ ‎ ∴∠EDC=∠ECD=30o ， ∴∠ADC=90o． 8分 ‎ ∴在Rt△ADC中，AD=a，∠ACD=30 o ， ∴ CD=．‎ ‎∵N为DC中点， ‎ ‎∴， ∴． 9分 ‎∵△ADE，△ABC，△AMN为等边三角形，‎ ‎∴S△ADE∶S△ABC∶ S△AMN 10分 解法二：△AMN是等边三角形．理由如下： 5分 ‎∵△ABE ≌ △ACD，M、N分别是BE、CN的中点，∴AM=AN，NC=MB．‎ ‎∵AB=AC，∴△ABM ≌ △ACN，∴∠MAB=∠NAC ，‎ ‎∴∠NAM=∠NAC+∠CAM=∠MAB+∠CAM=∠BAC=60o ‎∴△AMN是等边三角形 7分 设AD=a，则AD=AE=DE= a，AB=BC=AC=‎‎2a 易证BE⊥AC，∴BE=，‎ ‎∴ ∴‎ ‎∵△ADE，△ABC，△AMN为等边三角形 ‎ ∴S△ADE∶S△ABC∶ S△AMN 10分