2017-2018学年黑龙江省哈尔滨市南岗区九年级上期末考试数学试题含答案

2017-2018学年黑龙江省哈尔滨市南岗区九年级上期末考试数学试题含答案

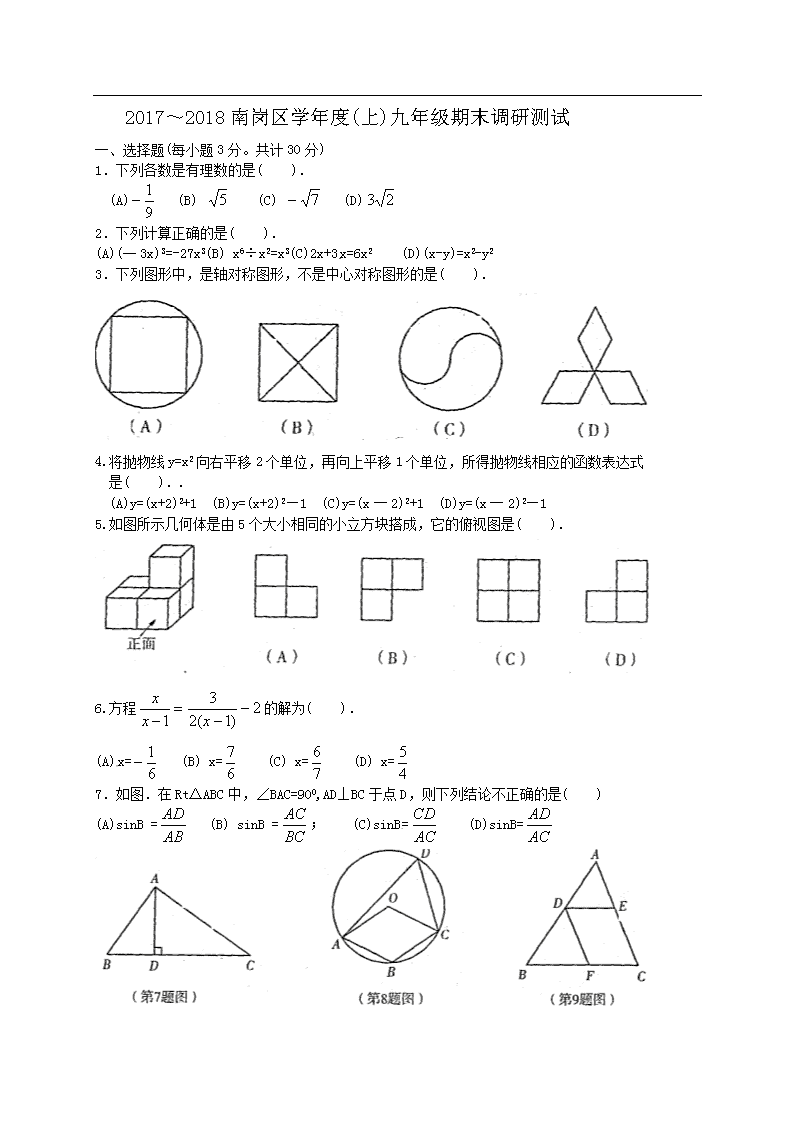
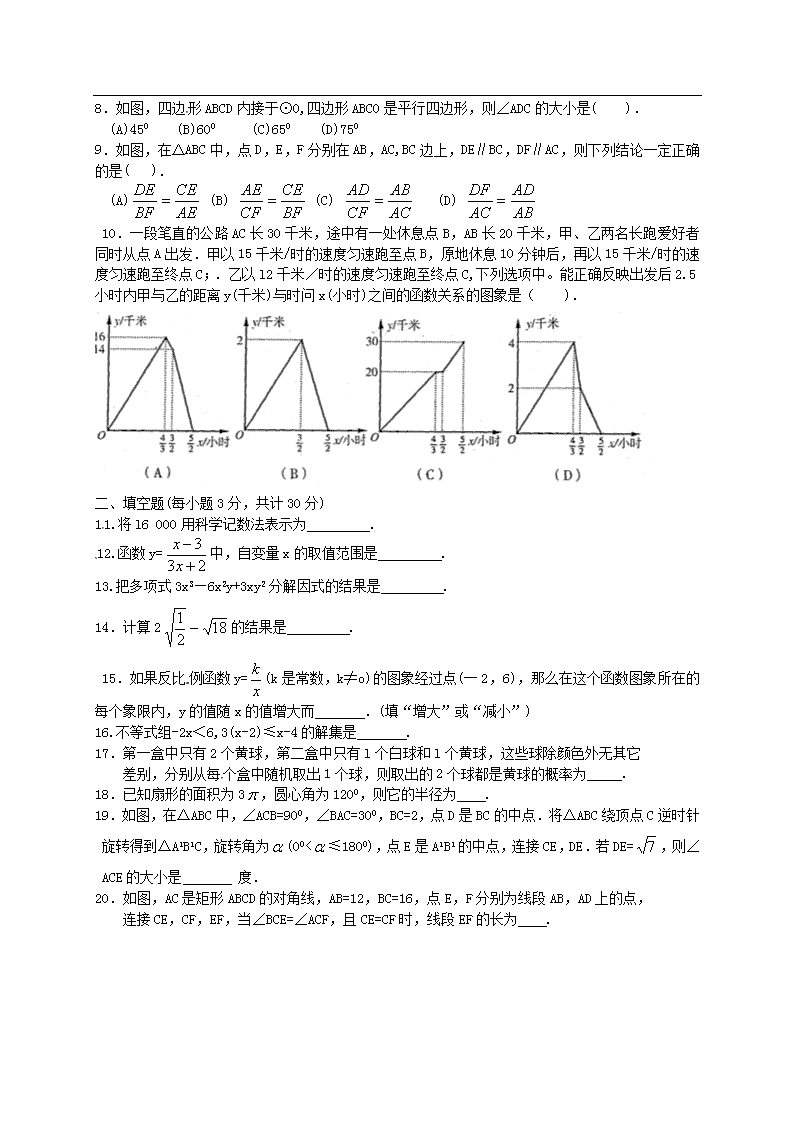
‎2017～2018南岗区学年度(上)九年级期末调研测试 一、选择题(每小题3分。共计30分)‎ ‎1．下列各数是有理数的是( )．‎ ‎ (A) (B) (C) (D)‎ ‎2．下列计算正确的是( )． ‎ ‎(A)(一3x)3=-27x3(B) x6÷x2=x3(C)2x+3x=6x2 (D)(x-y)=x2-y2‎ ‎3．下列图形中，是轴对称图形，不是中心对称图形的是( )．‎ ‎4.将抛物线y=x2向右平移2个单位，再向上平移1个单位，所得抛物线相应的函数表达式 ‎ 是( )．.[来源:Z_xx_k.Com]‎ ‎ (A)y=(x+2)2+1 (B)y=(x+2)2—1 (C)y=(x一2)2+1 (D)y=(x一2)2—1‎ ‎5.如图所示几何体是由5个大小相同的小立方块搭成，它的俯视图是( )．‎ ‎6.方程的解为( )．‎ ‎(A)x= (B) x= (C) x= (D) x=‎ ‎7．如图．在Rt△ABC中，∠BAC=900,AD⊥BC于点D，则下列结论不正确的是( )‎ ‎(A)sinB = (B) sinB =； (C)sinB= (D)sinB=‎ ‎8．如图，四边形ABCD内接于⊙O,四边形ABC0是平行四边形，则∠ADC的大小是( )．‎ ‎ (A)450 (B)600 (C)650 (D)750‎ ‎9．如图，在△ABC中，点D，E，F分别在AB，AC,BC边上，DE∥BC，DF∥AC，则下列结论一定正确的是( )．‎ ‎ (A) (B) (C) (D) ‎ ‎ 10．一段笔直的公路AC长30千米，途中有一处休息点B，AB长20千米，甲、乙两名长跑爱好者同时从点A出发．甲以15千米/时的速度匀速跑至点B，原地休息10分钟后，再以15千米/时的速度匀速跑至终点C；．乙以l2千米／时的速度匀速跑至终点C,下列选项中。能正确反映出发后2.5小时内甲与乙的距离y(千米)与时问x(小时)之间的函数关系的图象是（ )．‎ 二、填空题(每小题3分，共计30分)‎ ‎11.将l6 000用科学记数法表示为 .‎ ‎12.函数y=中，自变量x的取值范围是 .‎ ‎13.把多项式3x3—6x2y+3xy2分解因式的结果是 .‎ ‎14．计算2的结果是 .‎ ‎ 15．如果反比例函数y=(k是常数，k≠o)的图象经过点(一2，6)，那么在这个函数图象所在的每个象限内，y的值随x的值增大而 ．(填“增大”或“减小”)‎ ‎16.不等式组-2x＜6,3(x-2)≤x-4的解集是 .‎ ‎17．第一盒中只有2个黄球，第二盒中只有l个白球和l个黄球，这些球除颜色外无其它 ‎ 差别，分别从每个盒中随机取出1个球，则取出的2个球都是黄球的概率为 .‎ ‎18．已知扇形的面积为3，圆心角为1200，则它的半径为 .‎ ‎19．如图，在△ABC中，∠ACB=900，∠BAC=300，BC=2，点D是BC的中点．将△ABC绕顶点C逆时针旋转得到△A1B1C，旋转角为(00<≤1800)，点E是A1B1的中点，连接CE，DE．若DE=，则∠ACE的大小是 度．‎ ‎20．如图，AC是矩形ABCD的对角线，AB=12，BC=16，点E，F分别为线段AB，AD上的点，‎ ‎ 连接CE，CF，EF，当∠BCE=∠ACF，且CE=CF时，线段EF的长为 .‎ 三、解答题(第21—22题各7分，第23—24题各8分，第25—27题各l0分，共计60分)‎ ‎21．(本题7分)先化简，再求代数式的值，其中x=3tan300‎ ‎22．(本题7分) ‎ ‎ 如图，在平面直角坐标系中，点0为坐标原点，已知△ABC三个顶点的坐标分别为 A(-4，O)，b(-3，-3)，C(一l，一3) ‎ ‎ (1)画出△ABC 关于x轴对称的△ADE(其中点B，C的对称点分别为点D、E)；‎ ‎ (2)画出△ABC 关于原点成中心对称的△FGH(其中A、B、C的对称点分别为点F，G，)，‎ 连接EF,并直接写出线段EF的长．‎ ‎23．(本题8分) ‎ ‎ 为了解某校学生的课余兴趣爱好情况，某调查小组设计了“阅读”、“打球”、“书法”和“其他”四个选项，用随机抽样的方法调查了该校部分学生的课余兴趣爱好情况(每个学生必须选一项且只能选一项)，并根据调查结果绘制了如下统计图：‎ ‎ 根据统计图所提供的信息，解答下列问题：‎ ‎ (1)本次调查共抽取了多少名学生?‎ ‎ (2)补全条形统计图；‎ ‎ (3)该校共有l 800名学生，请根据统计结果估计该校课余兴趣爱好为“打球”的学生多少名．‎ ‎24．(本题8分)‎ ‎ 已知：在平行四边形ABCD中，点0是边BC的中点，连接D0并延长交AB延长线于 点E，连接BD，EC．‎ ‎ (1)如图l，求证：四边形BECD是平行四边形；‎ ‎ (2)如图2，四边形BECD是矩形，请探究∠BOD与∠A的数量关系，写出你的探究结论，‎ 并加以证明．‎ ‎25．(本题l0分】‎ 为了迎接十一国庆节，现要求甲、乙两队赶制小红旗：已知甲队的工作效率是乙队工作 效率的2倍，若两队各单独赶制600面小红旗，则甲队比乙队少用6天完成．[来源:Z.xx.k.Com][来源:Z.xx.k.Com]‎ ‎ (1)问甲、乙两队每天各能制作多少面小红旗?‎ ‎ (2)已知甲队、乙队每天的制作费用分别是400元、260元，若要求赶制小红旗的总数量为2 200面，且总费用不超过10 000元，问至少应安排甲队制作多少天？‎ ‎26.(本题l0分)‎ 已知：AB是⊙O的直径，弦CD⊥AB，垂足为点E(E在线段A0上)，点F是弧BD上的一个 动点，连接AF交CD于点G，过点F作⊙O 的切线交CD延长线于点H。[来源:学§科§网]‎ ‎(1)如图l，求证：∠H=2∠A；‎ ‎(2)如网2，若AE=2，DE=4，求线段0A的长；‎ ‎(3)如图3，存(2)的条件下，连接EF，若∠BEF=∠HEF，求线段EH的长．‎ ‎27．(本题l0分)‎ ‎ 如图，在平面直角坐标系中，点0为坐标原点，直线y=与x轴交于点A，与y轴交于点B，抛物线经过A，B两点．[来源:Zxxk.Com]‎ ‎ (1)求抛物线的解析式；‎ ‎ (2)点C为第三象限内抛物线上一点．连接AC，BC，设点C的横坐标为t．△ABC的面积为S，求S与t之间的函数关系式(不要求写出自变量t的取值范围)；‎ ‎ (3)在(2)的条件下，点D在直线AB上，点E在y轴上且位于点B的下方，若以点B，C，D，E为顶点的四边形是菱形，求△ABC的面积．‎