二次函数小结与复习（2）　　教案

二次函数小结与复习（2）　　教案

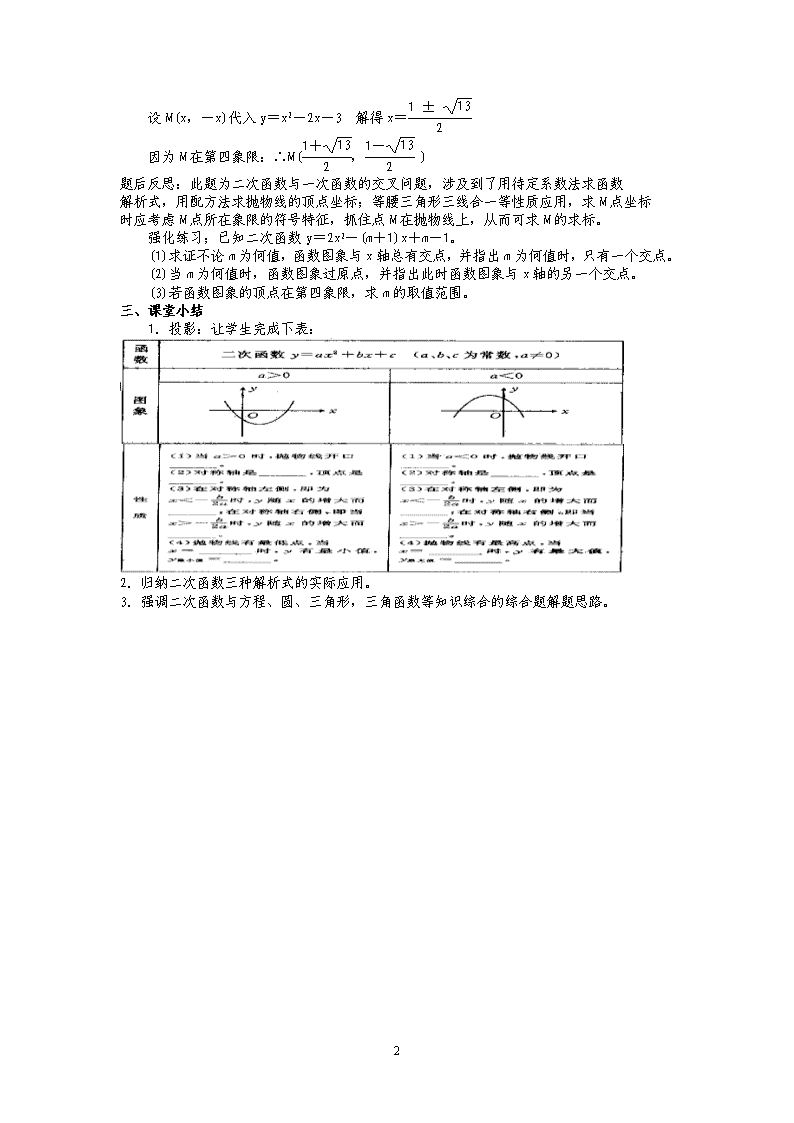
教学时间 课题 ‎《二次函数》小结与复习（2）‎ 课型 新授课 教 学 目 标 知　识 和 能　力 会用待定系数法求二次函数的解析式，能结合二次函数的图象掌握二次函数的性质，能较熟练地利用函数的性质解决函数与圆、三角形、四边形以及方程等知识相结合的综合题。‎ 过　程 和 方　法 情　感 态　度 价值观 教学重点 用待定系数法求函数的解析式、运用配方法确定二次函数的特征。‎ 教学难点 会运用二次函数知识解决有关综合问题。‎ 教学准备 教师 多媒体课件 学生 ‎“五个一”‎ 课堂教学程序设计 一、例题精析，强化练习，剖析知识点 ‎ 用待定系数法确定二次函数解析式．‎ ‎ 例：根据下列条件，求出二次函数的解析式。‎ ‎ (1)抛物线y＝ax2＋bx＋c经过点(0，1)，(1，3)，(－1，1)三点。‎ ‎ (2)抛物线顶点P(－1，－8)，且过点A(0，－6)。‎ ‎ (3)已知二次函数y＝ax2＋bx＋c的图象过(3，0)，(2，－3)两点，并且以x＝1为对称轴。‎ ‎ (4)已知二次函数y＝ax2＋bx＋c的图象经过一次函数y＝－3/2x＋3的图象与x轴、y轴的交点；且过(1，1)，求这个二次函数解析式，并把它化为y＝a(x－h)2＋k的形式。学生活动：学生小组讨论，并让学生阐述解题方法。‎ 教师归纳：二次函数解析式常用的有三种形式： (1)一般式：y＝ax2＋bx＋c (a≠0)‎ ‎ (2)顶点式：y＝a(x－h)2＋k (a≠0) (3)两根式：y＝a(x－x1)(x－x2) (a≠0)‎ ‎ 当已知抛物线上任意三点时，通常设为一般式y＝ax2＋bx＋c形式。‎ ‎ 当已知抛物线的顶点与抛物线上另一点时，通常设为顶点式y＝a(x－h)2＋k形式。‎ ‎ 当已知抛物线与x轴的交点或交点横坐标时，通常设为两根式y＝a(x－x1)(x－x2)‎ ‎ 强化练习：已知二次函数的图象过点A(1，0)和B(2，1)，且与y轴交点纵坐标为m。‎ ‎ (1)若m为定值，求此二次函数的解析式；‎ ‎ (2)若二次函数的图象与x轴还有异于点A的另一个交点，求m的取值范围。‎ 二、知识点串联，综合应用 ‎ 例：如图，抛物线y＝ax2＋bx＋c过点A(－1，0)，且经过直线y＝x－3与坐标轴的两个交点B、C。‎ ‎ (1)求抛物线的解析式；‎ ‎ (2)求抛物线的顶点坐标，‎ ‎ (3)若点M在第四象限内的抛物线上，且OM⊥BC，垂足为D，求点M的坐标。‎ ‎ 学生活动：学生先自主分析，然后小组讨论交流。教师归纳：‎ ‎ (1)求抛物线解析式，只要求出A、B，C三点坐标即可，设y＝x2－2x－3。‎ ‎ (2)抛物线的顶点可用配方法求出，顶点为(1，－4)。‎ ‎ (3)由|0B|＝|OC|＝3 又OM⊥BC。‎ ‎ 所以，OM平分∠BOC 2‎ ‎ 设M(x，－x)代入y＝x2－2x－3 解得x＝ ‎ 因为M在第四象限：∴M(， )‎ 题后反思：此题为二次函数与一次函数的交叉问题，涉及到了用待定系数法求函数 解析式，用配方法求抛物线的顶点坐标；等腰三角形三线合一等性质应用，求M点坐标 时应考虑M点所在象限的符号特征，抓住点M在抛物线上，从而可求M的求标。‎ ‎ 强化练习；已知二次函数y＝2x2－(m＋1)x＋m－1。‎ ‎(1)求证不论m为何值，函数图象与x轴总有交点，并指出m为何值时，只有一个交点。‎ ‎ (2)当m为何值时，函数图象过原点，并指出此时函数图象与x轴的另一个交点。‎ ‎ (3)若函数图象的顶点在第四象限，求m的取值范围。‎ 三、课堂小结 ‎ 1．投影：让学生完成下表：‎ ‎2．归纳二次函数三种解析式的实际应用。‎ ‎3．强调二次函数与方程、圆、三角形，三角函数等知识综合的综合题解题思路。‎ 2‎