- 2021-11-11 发布 |
- 37.5 KB |
- 6页

申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2019九年级数学上册 第二十四章 圆 24圆心角
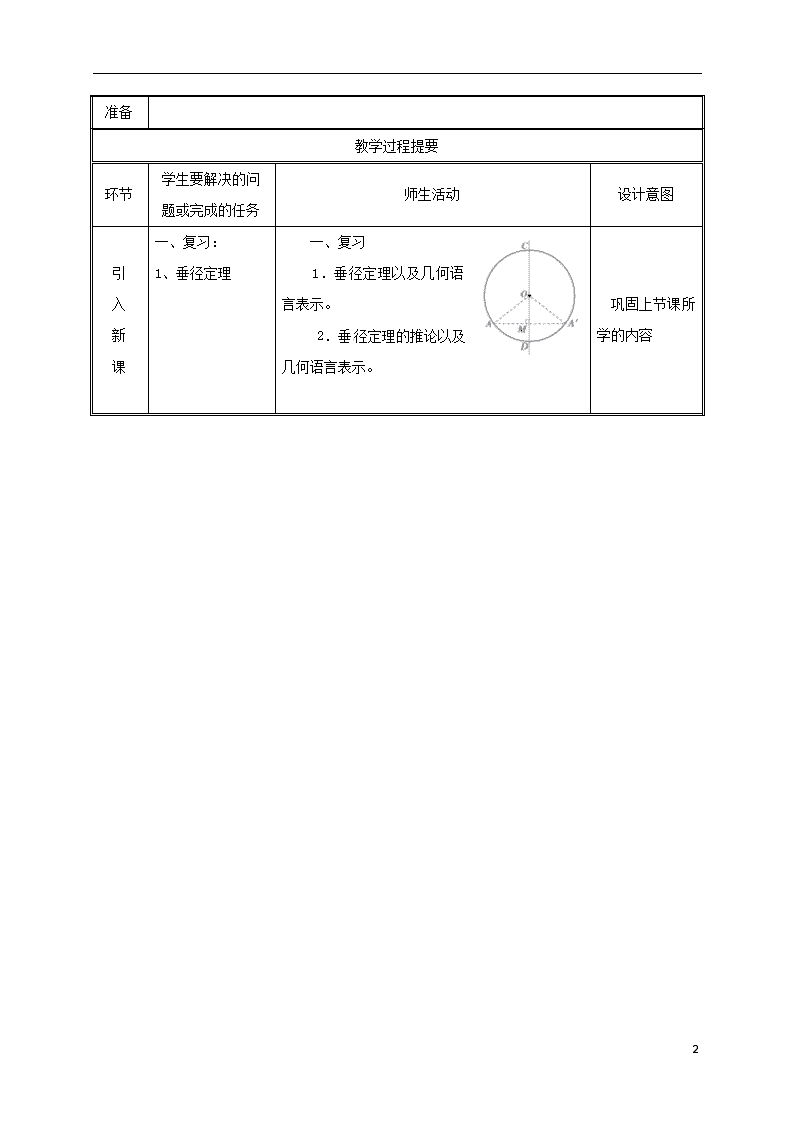
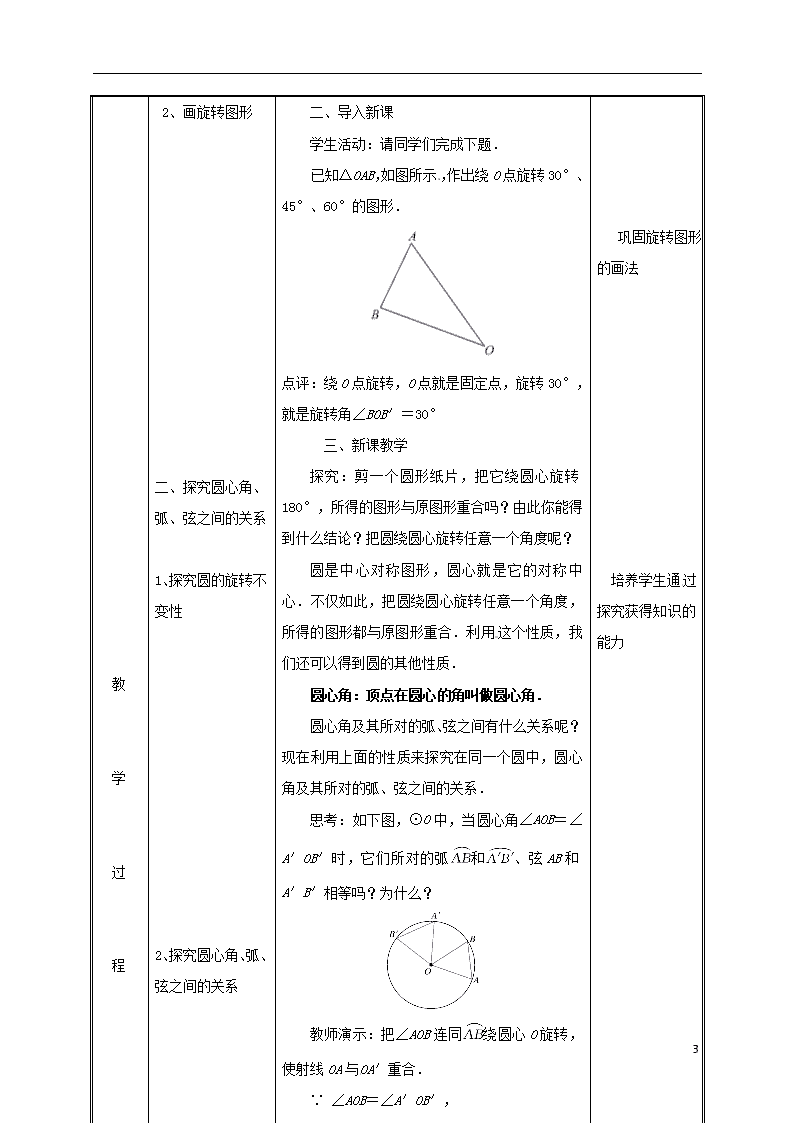
弧、弦、圆心角 课题:24.1.3 弧、弦、圆心角 课时 1 课 时 教学设计 课 标 要 求 理解圆心角的概念,圆心角、弧、弦之间的关系 教 材 及 学 情 分 析 1、 教材分析: 圆是平面几何中最重要的图形之一,它不仅在几何中有重要地位,而是进一步学习数学以及其他学科的重要基础。圆的许多性质,比较集中的反映了事物内部两边变和质变的关系,一般和特殊的关系、矛盾对立统一的关系。所以本章教学在初中数学教学中有重要地位。 2、 学情分析 学生在学习本章之前,已通过折叠、对称、平移、旋转、推理证明等方式认识了许多图形的性质,积累了大量的空间与图形的经验.本章是在学习了这些直线型图形的有关性质的基础上,进一步来探索一种特殊的曲线──圆的有关性质.通过本章的学习,对学生今后继续学习数学,尤其是逐步树立分类讨论的数学思想、归纳的数学思想起着良好的铺垫作用.本章的学习是高中的数学学习,尤其是圆锥曲线的学习的基础性工程. 课 时 教 学 目 标 1.了解圆的旋转对称性,掌握圆心角的概念. 2.掌握弧、弦、圆心角之间的关系,并能运用这些关系解决有关证明和计算的问题. 重点 弧、弦、圆心角之间的关系 难点 探索定理和推导及其应用 教法学法 指导 探究法 归纳法 练习法 教具 课件 6 准备 教学过程提要 环节 学生要解决的问 题或完成的任务 师生活动 设计意图 引 入 新 课 一、 复习: 1、垂径定理 一、复习 1.垂径定理以及几何语言表示。 2.垂径定理的推论以及几何语言表示。 巩固上节课所学的内容 6 教 学 过 程 2、画旋转图形 二、探究圆心角、弧、弦之间的关系 1、探究圆的旋转不变性 2、探究圆心角、弧、弦之间的关系 二、导入新课 学生活动:请同学们完成下题. 已知△OAB,如图所示,作出绕O点旋转30°、45°、60°的图形. 点评:绕O点旋转,O点就是固定点,旋转30°,就是旋转角∠BOB′=30° 三、新课教学 探究:剪一个圆形纸片,把它绕圆心旋转180°,所得的图形与原图形重合吗?由此你能得到什么结论?把圆绕圆心旋转任意一个角度呢? 圆是中心对称图形,圆心就是它的对称中心.不仅如此,把圆绕圆心旋转任意一个角度,所得的图形都与原图形重合.利用这个性质,我们还可以得到圆的其他性质. 圆心角:顶点在圆心的角叫做圆心角. 圆心角及其所对的弧、弦之间有什么关系呢?现在利用上面的性质来探究在同一个圆中,圆心角及其所对的弧、弦之间的关系. 思考:如下图,⊙O中,当圆心角∠AOB=∠A′OB′时,它们所对的弧和、弦AB和A′B′相等吗?为什么? 教师演示:把∠AOB连同绕圆心O旋转,使射线OA与OA′重合. ∵ ∠AOB=∠A′OB′, ∴ 射线OB与OB′重合. 又 OA=OA′、OB=OB′, ∴ 点A与A′重合,点B与B′重合. 因此,与重合,AB与A′B′重合.即=,AB=A′B′. 这样,我们就得到下面的定理: 在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦也相等. 同样,还可以得到: 在同圆或等圆中,如果两条弧相等,那么它们所对的圆心角相等,所对的弦相等; 在同圆或等圆中,如果两条弦相等,那么它们所对的圆心角相等,所对的弧相等. 巩固旋转图形的画法 培养学生通过探究获得知识的能力 6 教 学 过 程 四、用知识解决问题 五、练习: 四、实例探究 例 如图,在⊙O中,=,∠ACB=60°. 求证:∠AOB=∠BOC=∠AOC. 证明:∵ =, ∴ AB=AC,△ABC是等腰三角形. 又 ∠ACB=60°, ∴ △ABC是等边三角形,AB=BC=CA. ∴ ∠AOB=∠BOC=∠AOC. 五、 练习: 1. 如图,AB、CD是⊙O的两条弦. (1)如果AB=CD,那么___________,_________________. (2)如果弧AB=弧CD,那么____________,______________. (3)如果∠AOB=∠COD,那么_____________,____________. C A B D E F O (4)如果AB=CD,OE⊥AB于E,OF⊥CD于F,OE与OF相等吗?为什么? A B C D E 2. 如图,AB是⊙O的直径,弧BC=弧CD=弧DE, ∠COD=35°,求∠AOE的度数. 巩固所学知识 通过本题知道弦和弦心距之间的关系:弦相等,弦心距也相等。 6 小 结 这节课你学到了什么? 板 书 设 计 24.1.3 弧、弦、圆心角 1.圆心角概念. 2.在同圆或等圆中,如果两个圆心角、两条弧、两条弦中有一组量相等,那么它们所对应的其余各组量都部分相等,及其它们的应用. 作 业 设 计 绩优学案 1、必做题:1——8题 2、选做题:9题 6 教 学 反 思 6查看更多