2020九年级数学上册 第3章 圆的基本性质 3

2020九年级数学上册 第3章 圆的基本性质 3

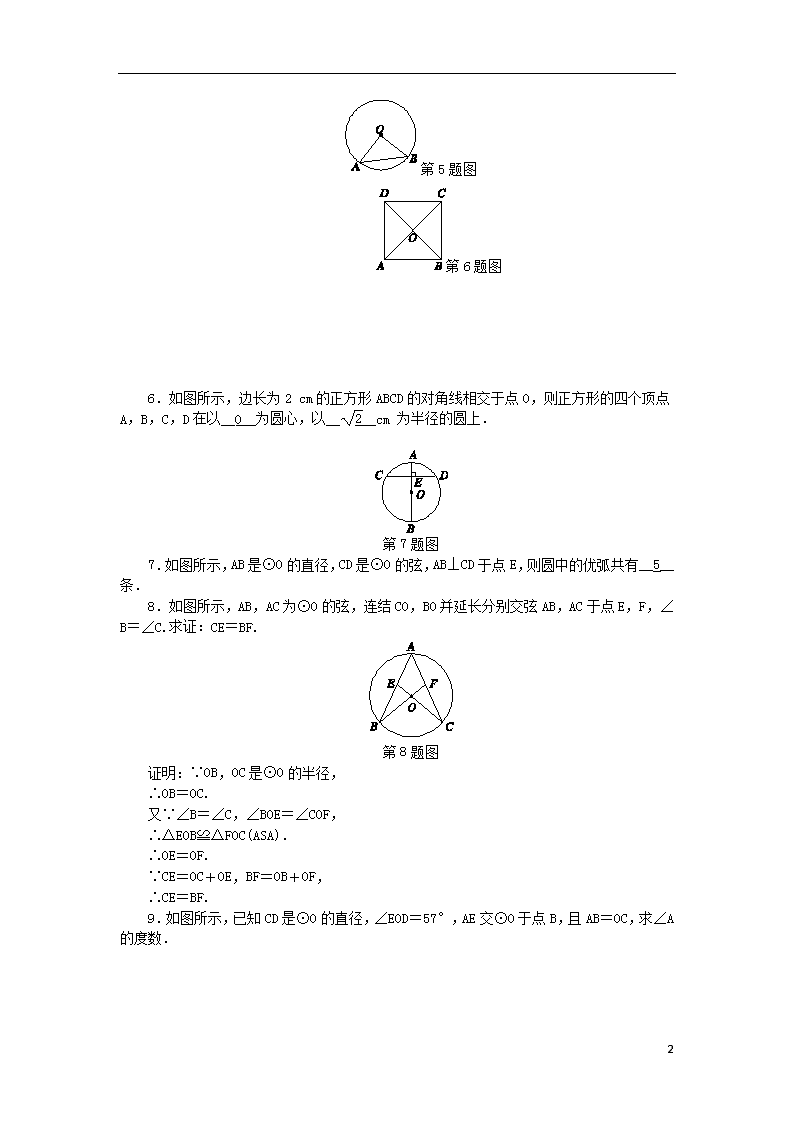
第3章　圆的基本性质 ‎3.1　圆(1)(见A本21页)‎ A　练就好基础　基础达标 ‎1．下列语句中，不正确的是(　C　)‎ A．直径是弦 B．经过圆内一定点可以作无数条弦 C．半圆不是弧 D．等弧所在的圆为同圆或等圆 ‎2．已知⊙O的半径是5，点A到圆心O的距离是7，则点A与⊙O的位置关系是(　C　)‎ A．点A在⊙O上 B．点A在⊙O内 C．点A在⊙O外 D．点A与圆心O重合 第3题图 ‎3．如图所示，点A，O，D以及点B，O，C分别在一条直线上，则圆中弦的条数是(　B　)‎ A．2 B．‎3 ‎ C．4 D．5‎ ‎4．在数轴上，点A所表示的实数为3，点B所表示的实数为a，⊙A的半径为2，下列说法中不正确的是(　A　)‎ A．当a＜5时，点B在⊙A内 B．当1＜a＜5时，点B在⊙A内 C．当a＜1时，点B在⊙A外 D．当a＞5时，点B在⊙A外 ‎5．如图所示，OA，OB是圆的两条半径，∠OAB＝45°，AO＝5，则AB＝__5__．‎ 4‎ 第5题图 ‎　　　　第6题图 ‎6．如图所示，边长为‎2 cm的正方形ABCD的对角线相交于点O，则正方形的四个顶点A，B，C，D在以__O__为圆心，以____cm 为半径的圆上．‎ 第7题图 ‎7．如图所示，AB是⊙O的直径，CD是⊙O的弦，AB⊥CD于点E，则圆中的优弧共有__5__条．‎ ‎8．如图所示，AB，AC为⊙O的弦，连结CO，BO并延长分别交弦AB，AC于点E，F，∠B＝∠C.求证：CE＝BF.‎ 第8题图 证明：∵OB，OC是⊙O的半径，‎ ‎∴OB＝OC.‎ 又∵∠B＝∠C，∠BOE＝∠COF，‎ ‎∴△EOB≌△FOC(ASA)．‎ ‎∴OE＝OF.‎ ‎∵CE＝OC＋OE，BF＝OB＋OF，‎ ‎∴CE＝BF.‎ ‎9．如图所示，已知CD是⊙O的直径，∠EOD＝57°，AE交⊙O于点B，且AB＝OC，求∠A的度数．‎ 4‎ 第9题图 解：连结OB，∵AB＝OC，∴AB＝OB，‎ ‎∴∠BOA＝∠BAO，‎ ‎∴∠OEA＝∠OBE＝2∠A，‎ ‎∴∠EOD＝3∠A.‎ ‎∵∠EOD＝57°，‎ ‎∴∠A＝19°.‎ ‎10．如图所示，已知两个同心圆，大圆的弦AB交小圆于C，D两点．‎ 求证：AD＝BC.‎ 第10题图 证明：由题意得OC＝OD，OA＝OB，∴∠A＝∠B，‎ ‎∠OCD＝∠ODC，‎ ‎∴△OAD≌△OBC(AAS)，‎ ‎∴AD＝BC.‎ B　更上一层楼　能力提升 ‎11．点P与定圆上最近点的距离为‎4 cm，与最远点的距离为‎9 cm，则圆的半径为(　C　)‎ A．‎2.5 cm 　　 B．‎‎6.5 cm C．‎2.5 cm 或 ‎6.5 cm 　　 D．‎‎13 cm ‎12．如图所示，AB，MN是⊙O的互相垂直的直径，点P在上且不与A，M重合，过点P作AB，MN的垂线，垂足分别是D，C，当P点在上移动时，矩形PCOD的形状、大小随之变化，则PC2＋PD2的值(　C　)‎ A．逐渐变大 B．逐渐变小 C．不变 D．不能确定 第12题图 ‎　　　　　第13题图 ‎13．如图所示，⊙O的半径OA＝6，以A为圆心，OA为半径的弧交⊙O于点B，C，‎ 4‎ 则BC的长是__6__．‎ ‎14．如图所示，已知△ABC，AC＝3，BC＝4，∠C＝90°，以点C为圆心作⊙C，半径为r.‎ ‎(1)点A，B在⊙C外，则r满足__0＜r＜3__；‎ ‎(2)点A在⊙C内，点B在⊙C外，则r满足 __3＜r＜4__．‎ 第14题图 ‎15．如图所示，AC，BD是⊙O的两条直径．‎ 求证：四边形ABCD为矩形．‎ 第15题图 证明：∵OA＝OC，OB＝OD，∴四边形ABCD为平行四边形．‎ 又∵AC＝AD＋OC，BD＝BO＋OD，‎ ‎∴AC＝BD，∴四边形ABCD为矩形．‎ C　开拓新思路　拓展创新 ‎16．如图所示，点A，B和点C，D分别在同心圆上，且∠AOB＝∠COD，BC与AD相等吗？为什么？‎ 第16题图 解：BC与AD相等．‎ 证明△AOD≌△BOC可得．‎ ‎17．如图所示，已知矩形ABCD的边AB＝5，AD＝12.‎ ‎(1)若以点A为圆心、12为半径作圆，试判断点B，C，D与⊙A的位置关系；‎ ‎(2)若以C点为圆心，使A，B，D三点中至少有一个点在圆内，且至少有一个点在圆外，求⊙C的半径r的取值范围；‎ ‎(3)试猜想：矩形的四个顶点能在同一个圆上吗？如果在同一个圆上，是在怎样的圆上呢？‎ 第17题图 解：(1)点B在⊙A内，点C在⊙A外，点D在⊙A上．‎ ‎(2)5

查看更多