- 2021-11-11 发布 |
- 37.5 KB |
- 7页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
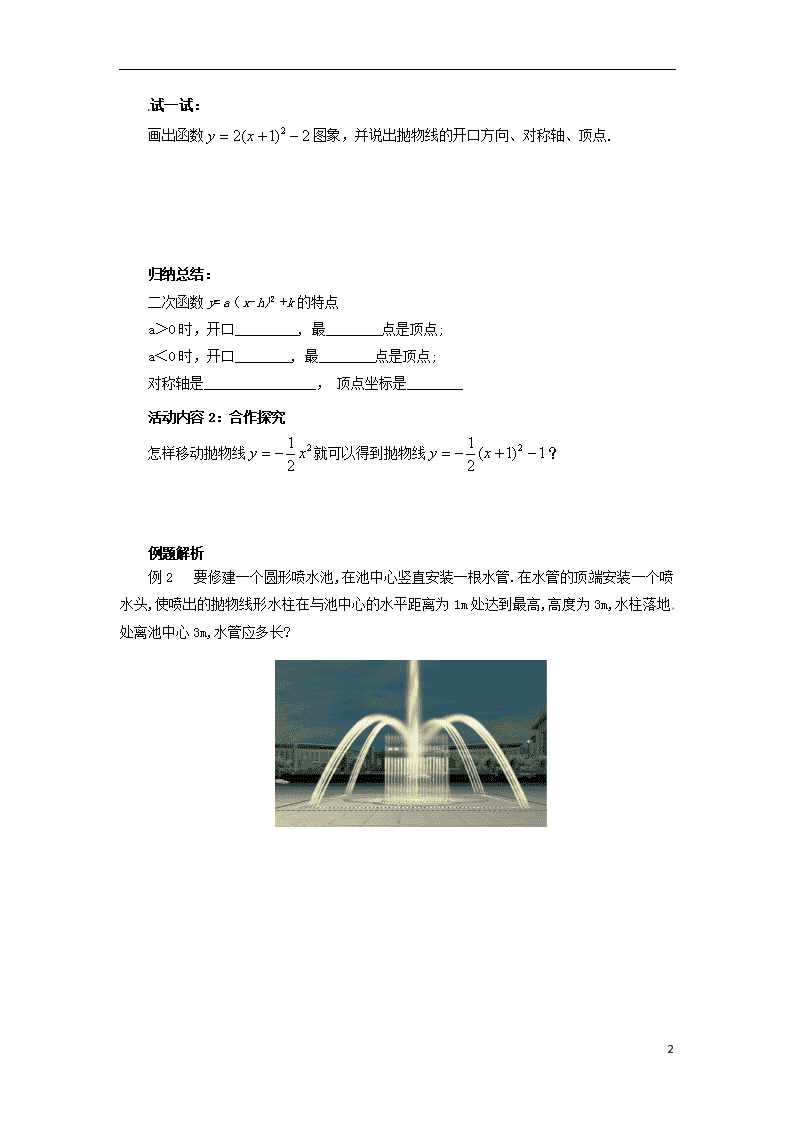
2020九年级数学上册 第二十二章 二次函数y=a(x-h)2+k的图象和性质(第3课时)导学案
22.1.3 二次函数y=a(x-h)²+k的图象和性质 第3课时 一、学习目标: 1、会用描点法画出y=a(x-h)2+k (a ≠0)的图象; 2、掌握二次函数y=a(x-h)2+k (a ≠0)的图象的性质并会应用; 3、理解y=a(x-h)2+k (a ≠0)与y=ax2 (a ≠0)之间的联系. 二、学习重难点: 重点:会用描点法画出y=a(x-h)2+k (a ≠0)的图象; 难点:掌握二次函数y=a(x-h)2+k (a ≠0)的图象的性质并会应用. 探究案 三、教学过程 活动1:小组合作 例1 画出函数的图像.指出它的开口方向、顶点与对称轴. 7 试一试: 画出函数图象,并说出抛物线的开口方向、对称轴、顶点. 归纳总结: 二次函数y=a(x-h)2 +k的特点 a>0时,开口_________, 最________点是顶点; a<0时,开口________, 最________点是顶点; 对称轴是________________, 顶点坐标是________ 活动内容2:合作探究 怎样移动抛物线就可以得到抛物线? 例题解析 例2 要修建一个圆形喷水池,在池中心竖直安装一根水管.在水管的顶端安装一个喷水头,使喷出的抛物线形水柱在与池中心的水平距离为1m处达到最高,高度为3m,水柱落地处离池中心3m,水管应多长? 7 练一练 1、请回答抛物线y = 4(x-3)2+7由抛物线y=4x2怎样平移得到? 2、如果一条抛物线的形状与形状相同,且顶点坐标是(4,-2),试求这个函数关系式. 随堂检测 1.完成下列表格: 二次函数 开口方向 对称轴 顶点坐标 y=2(x+3)2+5 y=-3(x-1)2-2 y = 4(x-3)2+7 y=-5(2-x)2-6 2.如图是二次函数y=ax2+bx+c(a≠0)图象的一部分,x=-1是对称轴,有下列判断:①b-2a=0;②4a-2b+c<0;③a-b+c= -9a;④若(-3,y1),(,y2)是抛物线上两点,则y1>y2.其中正确的是( ) A.①②③ B.①③④ C.①②④ D.②③④ 7 3.求二次函数y=x2- 2x-1的顶点坐标、对称轴及其最值. 4、如图,在△ABC中,∠B=90°,AB=12mm,BC=24mm,动点P以2mm/s的速度从A向B移动,(不与B重合),动点Q以4mm/s的速度从B向C移动,(不与C重合),若P、Q同时出发,试问经过几秒后,四边形APQC的面积最小?并求出最小值. 课堂小结 通过本节课的学习在小组内谈一谈你的收获,并记录下来: 我的收获 ____________________________________________________________________________________________________________________________________________________ 7 参考答案 例1 解: 先列表, 再描点、连线 开口方向向下;对称轴是直线x=-1;顶点坐标是(-1,-1) 试一试: y= 2(x+1)2-2开口方向向上;对称轴是直线x=-1;顶点坐标是(-1,-2) 归纳总结 向上 低 向下 高 直线x=h (h,k) 合作探究 平移方法1: 向下平移1个单位向左平移1个单位 平移方法2 向左平移1个单位向下平移1个单位 7 例2 解:如图建立直角坐标系,点(1,3)是图中这段抛物线的顶点. 因此可设这段抛物线对应的函数是y = a( x - 1 )2 + 3(0≤x≤3). ∵这段抛物线经过点(3,0), ∴ 0= a( 3 - 1 )2 + 3. 解得: a =- 因此抛物线的解析式为: y = - ( x - 1 )2 +3 (0≤x≤3) 当x=0时,y=2.25. 答:水管长应为2.25m. 练一练 1. 答:由抛物线向上平移7个单位再向右平移3个单位得到的. 2. 随堂检测 1. 2. B 3. 解:y=x2-2x-1=x2-2x+1-1=(x-1)2-2, ∴ 顶点坐标为(1,-2),对称轴是直线x=1.当x=1,时,y最小值=-2. 4. 解:设运动那个时间为t秒,则 7 根据二次函数的性质,当秒时,函数有最小值为 S最小值=4×32-24×3+144=144-36=108mm2 7查看更多