2020-2021学年初三数学上册同步练习：圆周角

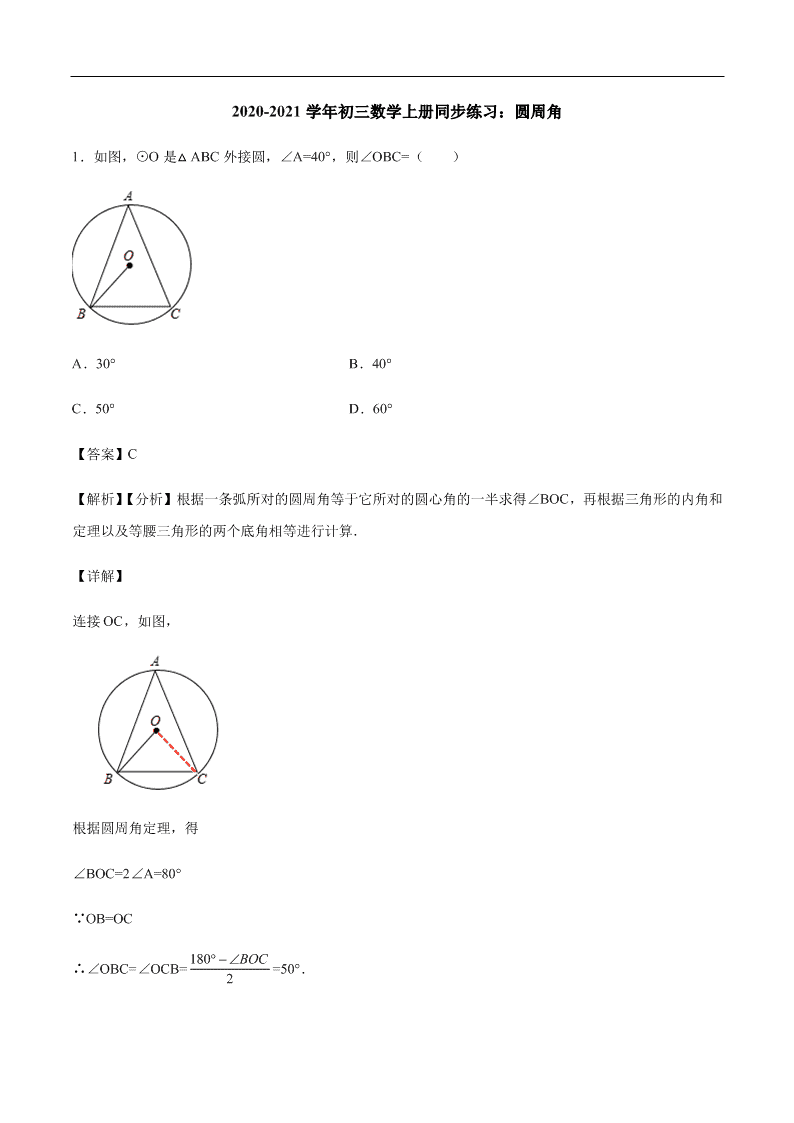
2020-2021学年初三数学上册同步练习：圆周角

2020-2021 学年初三数学上册同步练习：圆周角 1．如图，⊙O 是△ ABC 外接圆，∠A=40°，则∠OBC=（ ） A．30° B．40° C．50° D．60° 【答案】C 【解析】【分析】根据一条弧所对的圆周角等于它所对的圆心角的一半求得∠BOC，再根据三角形的内角和 定理以及等腰三角形的两个底角相等进行计算． 【详解】 连接 OC，如图， 根据圆周角定理，得 ∠BOC=2∠A=80° ∵OB=OC ∴∠OBC=∠OCB= 180 2 BOC   =50°． 故选 C． 【点评】本题考查了圆周角定理：一条弧所对的圆周角是它所对的圆心角的一半；也考查了等腰三角形的 性质以及三角形的内角和定理． 2．如图，AB 为⊙O 的直径，AC=2，BC=4，CD=BD=DE，则 CE=（ ） A．3﹣ B． 3 2 10 2  C． 3 1 0 2  D． 3 2 1 0 【答案】D 【解析】【分析】先根据勾股定理计算直径 AB= 2224 =2 5 ，作垂线 DP 和 DQ，根据角平分线的性质 得：DP=DQ，由全等可得 AP=AQ，设未知数列等式，可得 PC 和 BQ 的长，再根据等腰三角形的性质得： ∠DEC=∠DCE，根据外角性质得：∠ACE=∠ECB，则∠ACE=∠ECB=45°，作辅助线后可得：△ EFC 是等 腰直角三角形，设 EF=FC=a，则 CE= 2 a，AF=2-a，根据△ AFE∽△APD，列比例式可得 a 的值，求 CE 的长． 【详解】 ∵AB 是⊙O 的直径， ∴∠ACB=90°， ∵AC=2，BC=4， ∴AB= =2 ， ∵CD=BD， ∴ C D B D ， ∴∠CAD=∠BAD， 过 D 作 DP⊥AC 于 P，DQ⊥AB 于 Q，连接 OD， ∴PD=DQ， ∴Rt△ DPC≌Rt△ DQB（HL）， ∴CP=BQ， 易得△ APD≌△AQD， ∴AP=AQ， 设 PC=x，则 AP=2+x，AQ=AB-BQ=2 5 -x， ∴2+x=2 -x， x= -1， ∴BQ=CP= -1，OQ=1， Rt△ ODQ 中，DQ=PD= 22( 5) 1 =2， ∵DE=DC， ∴∠DEC=∠DCE， ∵∠DEC=∠CAD+∠ACE，∠DCE=∠ECB+∠ACE， ∴∠CAD+∠ACE=∠ECB+∠DCB， ∵ D C B C ， ∴∠CAD=∠DCB， ∴∠ACE=∠ECB， ∵∠ACB=90°， ∴∠ACE=∠ECB=45°， 过 E 作 EF⊥AP 于 F， ∴△EFC 是等腰直角三角形， 设 EF=FC=a，则 CE= 2 a，AF=2-a， ∵EF∥PD， ∴△AFE∽△APD， ∴ EFAF PDAP ＝ ， ∴ 2 2 251 aa  ＝ ， ∴a=3- 5 ， ∴CE= a= （3- ）=3 - 10 . 故选 D． 【点评】 本题是有关圆的计算问题，题意虽然简单，但有难度，考查了圆周角定理、勾股定理、三角形相似的判定 和性质，作辅助线构建等腰直角△ EFC 是关键． 3．如图，⊙O 的内接四边形 ABCD 两组对边的延长线分别交于点 E，F． （1）若∠E+∠F=α，求∠A 的度数（用含 α 的式子表示）； （2）若∠E+∠F=60°，求∠A 的度数． 【答案】（1）∠A=90°﹣ 1 2 α；（ 2）∠A=60°． 【解析】【分析】（1）根据圆内接四边形的性质得到∠A=∠BCF，再利用三角形外角性质得∠EBF=∠A+∠E， 由三角形内角和定理得∠EBF=180°-∠BCF-∠F，所以∠A+∠E=180-∠A-∠F，然后利用∠E+∠F=α 可得 ∠A=90°- α； （2）利用（1）中的结论进行计算． 【详解】 （1）∵四边形 ABCD 为⊙O 的内接四边形， ∴∠A=∠BCF， ∵∠EBF=∠A+∠E， 而∠EBF=180°﹣∠BCF﹣∠F， ∴∠A+∠E=180°﹣∠BCF﹣∠F， ∴∠A+∠E=180﹣∠A﹣∠F， 即 2∠A=180°﹣（∠E+∠F）， ∵∠E+∠F=α， ∴∠A=90°﹣ 1 2 α； （2）当 α=60°时，∠A=90°﹣ ×60°=60°． 【点评】本题考查了圆内接四边形的性质：圆内接四边形的对角互补；圆内接四边形的任意一个外角等于 它的内对角． 4．已知：如图，⊙O 的两条半径 OA⊥OB，C，D 是 AB 的三等分点，OC，OD 分别与 AB 相交于点 E，F． 求证：CD＝AE＝BF． 【答案】见解析 【解析】【分析】连接 AC、BD，由 C，D 是 的三等分点，可得 AC=CD=BD，∠AOC=∠COD=∠DOB=30°， 利用 SAS 可证明△ AOC≌△COD，即可得出∠ACO=∠OCD，根据等腰三角形的性质可得∠OEF＝∠OCD， 可证明 CD//AB，可得∠AEC＝∠OCD，即可证明∠ACO＝∠AEC．可得 AC=AE，同理可证 BD=BF，进而 可证明 CD＝AE＝BF． 【详解】 连接 AC、BD， ∵OA⊥OB， ∴∠AOB=90°， ∵OA=OB， ∴∠OAB=∠OBA=45°， ∵C，D 是 的三等分点， ∴AC=CD=BD，∠AOC=∠COD=∠DOB=30°， ∵∠AOC=∠COD，OA=OC=OD， ∴△AOC≌△COD， ∴∠ACO=∠OCD， ∵∠OEF＝∠OAE+∠AOE＝45°+30°＝75°，∠OCD= 2 80 01 3   =75°， ∴∠OEF＝∠OCD， ∴CD∥AB， ∴∠AEC＝∠OCD， ∴∠ACO＝∠AEC． 故 AC＝AE， 同理，BF＝BD． 又∵AC＝CD＝BD ∴CD＝AE＝BF． 【点评】本题主要考查了全等三角形的判定和性质、圆周角定理、等腰三角形的性质，在同圆或等圆中， ①圆心角相等，②所对的弧相等，③所对的弦相等，三项“知一推二”，一项相等，其余二项皆相等． 5．如图，在△ ABC 中，AB＝AC，AC 是⊙O 的弦，BC 交⊙O 于点 D，作∠BAC 的外角平分线 AE 交⊙O 于点 E，连接 DE．求证：DE＝AB． 【答案】见解析. 【解析】【分析】求出∠FAE=∠B=∠C，推出 AE∥BC，求出∠E=∠C=∠EDC=∠B，推出 AB∥ED，根据 平行四边形的性质和判定推出即可． 【详解】 ∵AB＝AC， ∴∠B＝∠C， ∴ 2FACBCB  ， ∵AE 平分∠FAC， ∴ 22FACFAEEAC ， ∴∠FAE＝∠B， ∴ AEBC∥ ， ∴ E EDC   ， ∵ E C B     ， ∴ EDAB∥ ， ∵AE∥BC， ∴四边形 ABDE 是平行四边形， ∴DE＝AB． 【点评】本题考查了圆周角定理，等腰三角形的性质，平行四边形的性质和判定，平行线的性质和判定的 应用，熟练掌握和灵活运用相关知识是解题的关键. 6．如图，已知 AB 是⊙O 的直径，弦 CD⊥AB 于点 E，点 M 在⊙O 上， MD   ． （1）判断 BC、MD 的位置关系，并说明理由； （2）若 AE＝16，BE＝4，求线段 CD 的长． 【答案】（1）BC∥MD，见解析；（2）CD 的长是 16． 【解析】【分析】（1）根据圆周角定理可得出∠M=∠D=∠CBM，由此即可得出结论； （2）先根据 AE=16，BE=4 得出 AB 的长，进而得出 OE 的长，连接 OC，根据勾股定理得出 CE 的长，进 而得出结论. 【详解】 （1）BC、MD 的位置关系是平行， 理由：∵∠M＝∠D， ∴ BD MC ， ∴∠M＝∠MBC， ∴BC∥MD； （2）连接 OC， ∵AB 是⊙O 的直径，弦 CD⊥AB 于点 E，AE＝16，BE＝4， ∴ 9020OECECEDABAEBE ， ， ， ∴ 10,6OCOBOEOBBE ， ∴ 228CEOCOE ， ∴ 2 1 6C D C E， 即线段 CD 的长是 16． 【点评】本题考查了圆周角定理、垂径定理、勾股定理，解题此类问题的关键是明确题意，根据所要证明 或求解的问题找出相应的条件，利用圆周角定理、垂径定理和勾股定理的相关知识解答． 7．如图，△ ABC 的三个顶点都在⊙O 上，AD 为⊙O 的直径，AE⊥BC 于点 E，交 ⊙O 于点 F．求证： 12 ． 【答案】见解析. 【解析】【分析】根据 AD 是⊙O 的直径，得出∠D+∠1=90°，再根据 AE⊥BC，得出∠2+∠ACB=90°，最 后根据同弧所对的圆周角相等得出∠C=∠D，即可得出答案． 【详解】 连接 BD， ∵AD 为⊙O 的直径， ∴∠ABD＝90°， ∴ 1 9 0D    ， ∵AE⊥BC， ∴∠AEC＝90°， ∴ 2 9 0 C     ， 由圆周角定理得，∠C＝∠D， ∴∠1＝∠2． 【点评】本题考查的是圆周角定理的应用，掌握在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于 这条弧所对的圆心角的一半．推论：半圆（或直径）所对的圆周角是直角是解题的关键． 8．如图，⊙O 是△ ABC 的外接圆，AD 是△ ABC 的高，AE 是⊙O 的直径，求证： BAE CAD   ． 【答案】见解析. 【解析】【分析】连接 BE，由直径所对的圆周角是直角以及直角三角形的性质可得∠BAE+∠E=90°， 90CAD ACB    ，由圆周角定理可得∠E=∠ACB，继而可得∠BAE=∠CAD． 【详解】 连接 BE， ∵AE 是⊙O 的直径， ∴∠ABE＝90°， ∴ 90BAE E   ， ∵ AD 是 ABC△ 边上的高， ∴ 90ADC ， ∴ 90CADACB  ， ∵∠E＝∠ACB， ∴∠BAE＝∠CAD． 【点评】本题考查的是圆周角定理及直角三角形的性质，熟知“在同圆或等圆中，同弧或等弧所对的圆周角 相等”是解答此题的关键．