相似三角形判定定理的证明学案1

相似三角形判定定理的证明学案1

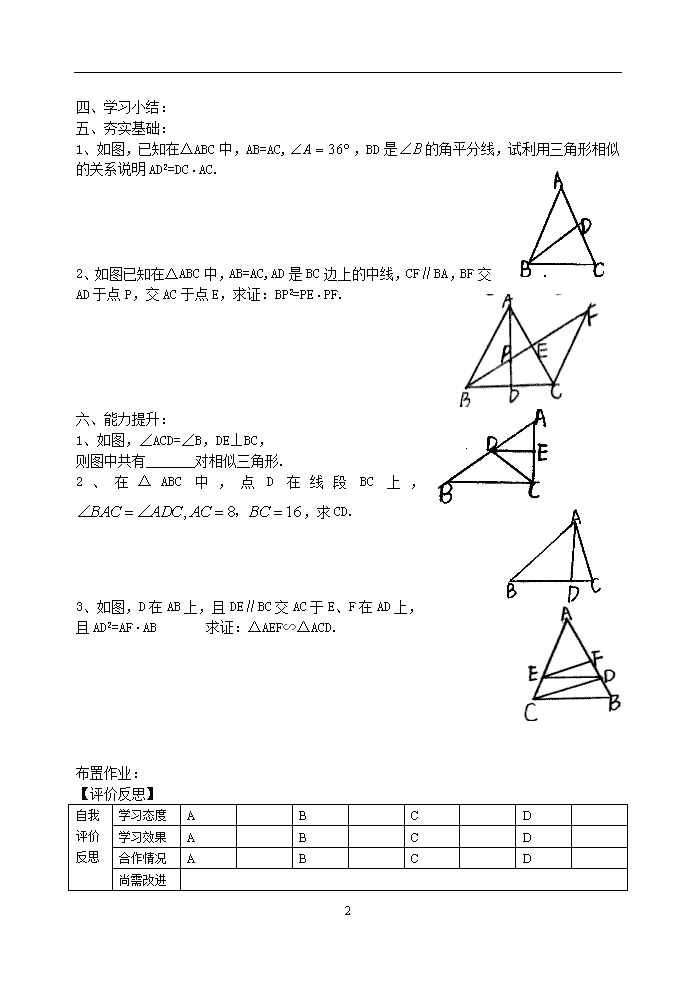
‎4.5 相似三角形判定定理的证明 主备：曹玉辉 副备：孙芬 李春贺 审核： ‎ 一、 学习准备：‎ 判定定理1：两角 的两三角形相似；‎ 判定定理2：两边 两个三角形相似；‎ 判定定理3： 的两三角形相似.‎ 二、学习目标：‎ ‎1、相似三角形的判定定理；‎ ‎2、相似三角形的判定定理的证明；‎ 三、自学提示：‎ 自主学习：‎ 独立证明三个判定定理。‎ 见书P99页。‎ 例题：‎ 例1、如图，在平行四边形，过点B作，垂足为E，连接AE,F为AE上一点，且.‎ ‎（1）求证：△ABF∽△EAD；‎ ‎（2）若AB=4，求AE的长；‎ ‎（3）在（1）（2）的条件下，若AD=3，求BF的长.‎ 变式演练：如图四边形ABCD是平行四边形，点F在BA的延长线上连结CF角AD于点E.‎ ‎（1）求证：△CDE∽△FAE；‎ ‎（2）当E是AD的中点，且BC=2CD时，求证：.‎ 例2、已知DE⊥AB，EF⊥BC求证：△DEF∽△ABC.‎ 3‎ 四、学习小结：‎ 五、夯实基础：‎ ‎1、如图，已知在△ABC中，AB=AC, ，BD是的角平分线，试利用三角形相似的关系说明AD2=DC·AC.‎ ‎2、如图已知在△ABC中，AB=AC,AD是BC边上的中线，CF∥BA，BF交AD于点P，交AC于点E，求证：BP2=PE·PF.‎ 六、能力提升：‎ ‎1、如图，∠ACD=∠B，DE⊥BC，‎ 则图中共有 对相似三角形.‎ ‎2、在△ABC中，点D在线段BC上，，求CD.‎ ‎3、如图，D在AB上，且DE∥BC交AC于E、F在AD上， ‎ 且AD2=AF·AB 求证：△AEF∽△ACD.‎ 布置作业：‎ ‎【评价反思】‎ 自我 评价 反思 学习态度 A B C D 学习效果 A B C D 合作情况 A B C D 尚需改进 3‎ 3‎