人教版中考数学二轮复习专题练习上函数与相似全等综合

人教版中考数学二轮复习专题练习上函数与相似全等综合

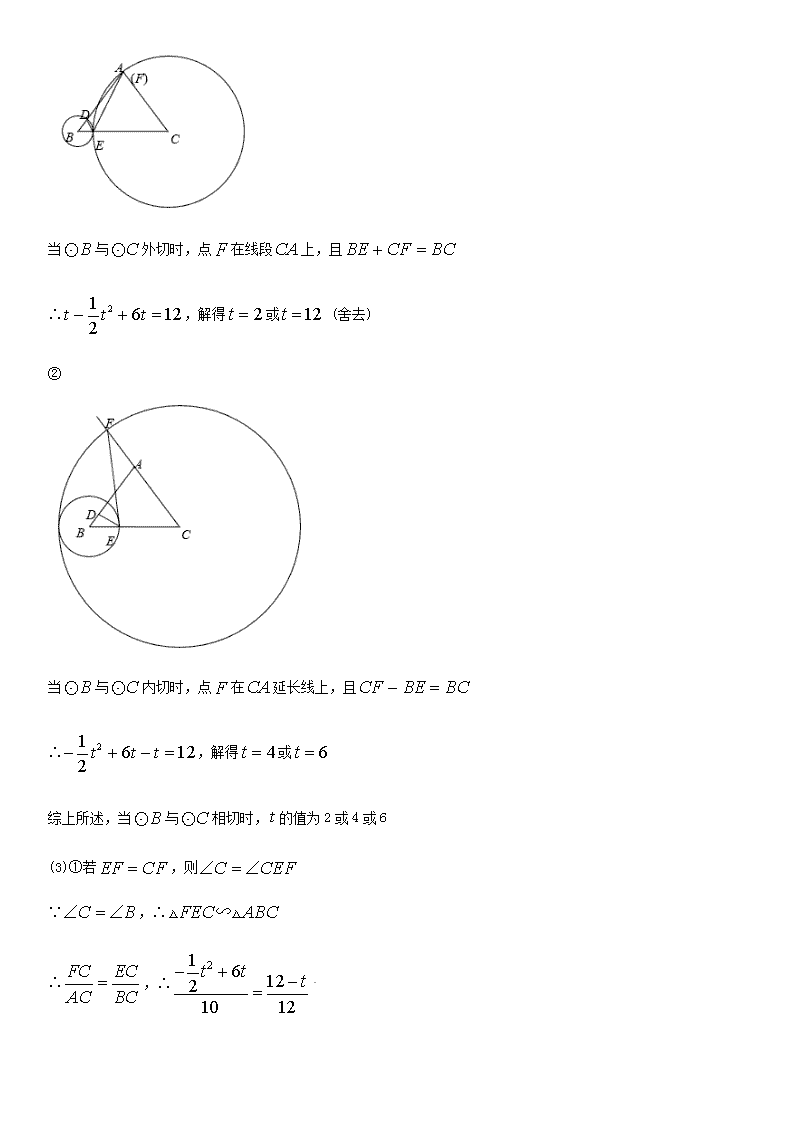
函数与相似全等综合 ‎1.如图，在 中， ， ，点 为 边上一点，且 ．动点 从点 出发，以 的速度沿线段 向终点 运动， 是射线 上的动点，且．设运动时间为，的长为．‎ ‎(1)求与之间的函数关系式及点运动路线的长；‎ ‎(2)当以点为圆心，长为半径的与以点为圆心，长为半径的相切时，求的值；‎ ‎(3)当为等腰三角形时，求的值．‎ 解析：(1)∵，∴‎ ‎∵，，‎ ‎∴，∴‎ ‎∴，∴‎ ‎∴‎ ‎∵‎ ‎∴的最大值为 ‎∴点运动路线的长为 ‎(2)‎ ‎①‎ 当与外切时，点在线段上，且 ‎∴，解得或 (舍去)‎ ‎②‎ 当与内切时，点在延长线上，且 ‎∴，解得或 综上所述，当与相切时，的值为2或4或6‎ ‎(3)①若，则 ‎∵，∴‎ ‎∴，∴‎ 解得或 (舍去)‎ ‎②若，则 ‎∵，∴‎ ‎∴，∴‎ 解得或 (舍去)‎ ‎③若，则 解得或 (舍去)‎ 综上所述，当为等腰三角形时，的值为 或2或 ‎ ‎2.如图，矩形中，点在边上，且与点、不重合，过点作的垂线与的延长线相交于点，连接，的中点为．‎ ‎(1)求证：；‎ ‎(2)若，，点在边上运动，设，，求与的函数关系式，并求线段长的最小值；‎ ‎(3)若，，，随着的大小的变化，点的位置也在变化．当点落在矩形内部时，求的取值范围．‎ 解析：‎ ‎(1)证明：∵四边形为矩形，∴‎ ‎∴‎ ‎∵，∴‎ ‎∴‎ ‎∴‎ 又∵‎ ‎∴‎ ‎(2)解：‎ ‎∵， ‎ 即，∴‎ ‎∴‎ 过点作于 ‎∵为的中点，∴为的中位线 ‎∴‎ ‎∴‎ 在中，‎ 即 ‎∵‎ ‎∴当时，有最小值 ‎∴线段长的最小值为 ‎(3)‎ 设与交于点，过点作于 ‎∵点落在矩形内部，∴‎ 由(2)知，为的中位线 ‎∴‎ ‎∴‎ ‎∵，∴‎ 即 ，∴‎ ‎∵，∴‎ ‎，即 ‎ ‎∴‎ ‎∴‎ ‎∵，∴‎ 解得 ‎3.已知中，，点是边上的一个动点，连接，过点作，垂足为点.‎ ‎(1)如图1，当经过的重心时，求证：； ‎ ‎(2)如图2，若厘米，，点从点向点运动(不与点、重合)，点的速度是厘米/秒，设点运动的时间为秒，的面积为平方厘米，求关于的函数解析式，并写出自变量的取值范围；‎ ‎(3)在(2)的条件下，若是以为腰的等腰三角形，求的面积．‎ 解析：‎ ‎(1)证明：∵经过的重心，∴为的中线 ‎∴，∴‎ 又∵，‎ ‎∴，又 ‎∴ ‎ ‎(2)解：‎ ‎∵ ， ，∴ ‎ 过点 作 于 ，则， ， ‎ ‎ ，‎ 由 ，得 ‎ ‎∴，即 ‎ ‎∴‎ ‎(3)①当 时，有 解得 ‎ 当时， (平方厘米)‎ ‎②当 时，有 ‎ 解得， (不合题意，舍去)‎ 当时， (平方厘米)‎ 综上所述，当 时， 的面积为 平方厘米；当 时， 的面积为 平方厘米 ‎4.如图，已知线段 长为12，点 、 在线段 上，且 ．动点 从点 出发沿线段 向点 移动(移动到点 停止)，分别以 、 为斜边在线段 同侧作等腰 和等腰 ，连接 ，设 ．‎ ‎(1)求线段 长的最小值；‎ ‎(2)当 为何值时， 的外接圆与 相切；‎ ‎(3)求四边形 的面积与的函数关系式；‎ ‎(4)设的中点为，直接写出整个运动过程中点移动的路径的长．‎ 解析：(1)‎ 作于，于，于 ‎∵，∴‎ ‎，‎ ‎∴‎ ‎∴‎ 当时，有最小值36‎ ‎∴线段长的最小值是6‎ ‎(2)作于， ‎ 可见在点由点向点移动过程中，点到的距离始终为3，而由(1)知线段的长随的变化而变化，当，即点运动到中点时，，而由题意可得，是直角三角形，所以点是外接圆的圆心，只有此时的外接圆才与相切 ‎∴当时，的外接圆与相切 ‎(3)延长、交于点 易知是等腰直角三角形，四边形是矩形 即 ‎(4)由(2)知点到的距离始终为3，所以随着点的移动，点的移动路径是一条平行于的线段 ‎∵，，∴‎ ‎∵点在线段上，∴‎ ‎∵‎ ‎∴当时，；当时，‎ ‎∴点移动的路径长为 ‎5.在中，, , ,点 在 上，并且 ,现有两个动点、 分别从 和点 同时出发，其中点 以 的速度，沿 向终点 移动；点以 的速度沿 向终点 移动.过点 作 交 于点 ，连结 .设动点运动时间为 秒.‎ ‎(1)用含 的代数式表示 、 的长度；‎ ‎(2)当点在 (不包括点 、 )上移动时，设 的面积为，求与的函数关系式，并写出自变量的取值范围；‎ ‎(3)当为何值时， 为直角三角形.‎ 解析：‎ ‎(1)‎ 在 中，∵ ， ，‎ ‎∴ ，‎ ‎∵ ，‎ ‎∴ 　‎ ‎∴，即，∴， ‎ ‎(2)∵ ， ,∴ ‎ ‎ 当点 在 上运动 秒后， ,‎ 则 即与的函数解析式为：，‎ 其中自变量的取值范围是： ‎ ‎(3)分两种情况讨论：‎ ‎①当 时，‎ ‎∴ ，‎ ‎∵ ‎ ‎∴ ‎ ‎∴,‎ 即，解得 解得 ‎ ‎②当 时，‎ ‎∵ ， ‎ ‎∴ ‎ ‎∴‎ 即 解得： ‎ 综上所述，当 为 秒或 秒时， 为直角三角形.‎ ‎6.如图，在梯形 中，，，，，点由 出发沿 方向匀速运动，速度为 ；同时，线段 由 出发沿 方向匀速运动，速度为 ，交于 ，连接 ．若设运动时间为 ．解答下列问题：‎ ‎(1)过作，交于．当为何值时，四边形是平行四边形？‎ ‎(2)设，求与之间的函数关系式，并求为何值时，有最大值，最大值是多少；‎ ‎(3)连接，在上述运动过程中，五边形的面积是否发生变化？说明理由．‎ 解析：(1)∵四边形是平行四边形．‎ ‎∴∴． ‎ 而，‎ ‎∴，‎ ‎∴．‎ ‎∴当，四边形是平行四边形 ‎(2)∵平行且等于，∴．‎ ‎∵，∴．‎ ‎∴．‎ ‎∴即．‎ ‎∴ ‎ ‎∵，∴．‎ ‎∴ ‎ ‎∴当时，有最大值5． ‎ ‎(3)在和中，‎ ‎ ‎ ‎∴‎ ‎ ‎ ‎ ．‎ ‎∴在运动过程中，五边形的面积不变．‎ ‎7.如图， 中， ， ，点 、 分别在边 、 上，且 ．直线 过点且 ，点 是射线 上一动点， 的延长线与直线 相交于点 ， 的延长线与射线 相交于点 ， 与 相 交于点 ，设 ．‎ ‎(1)求 的面积 关于 的函数关系式；‎ ‎(2)当 为何值时， ？‎ ‎(3)当 为等腰三角形时，直接写出 的长．‎ 解析：‎ ‎(1)‎ 过 作 于 ‎ ‎∵ ， ，∴‎ ‎∴‎ ‎∵ ，∴ ‎ ‎∵ ， ，∴ ‎ ‎∵ ，∴，‎ ‎∴ ， ，‎ 过 作 ，分别交 、 于点 、 ‎ 则，∴ ‎ ‎∴‎ ‎∴‎ ‎(2)‎ 过 作 于 ‎ ‎∵ ，∴ ‎ ‎∴ ，∴‎ ‎∴，∴ ， ‎ ‎∵ ，∴ ‎ ‎∵ ，∴ ‎ ‎∵ ，∴ ‎ ‎∴ ，∴‎ ‎∴，∴，∴‎ ‎∴‎ 即当时， ‎ ‎(3) 或 或 ‎ ‎7.如图，在 中， ， ， 为 的中点．‎ ‎(1)若 、 分别是 、 上的点，且 ，求证： ；‎ ‎(2)当点 、 分别从 、 两点同时出发，以每秒1个单位长度的速度沿 、 运动，到点 、 时停止；设 的面积为 ， 点运动的时间为 ，求与的函数关系式；‎ ‎(3)在(2)的条件下，点 、分别沿 、 的延长线继续运动，求此时与的函数关系式．‎ 解析：(1)证明：∵ ， ， 为 的中点 ‎∴ ‎ ‎∴ ‎ ‎∵ ，∴ ‎ ‎(2)解：依题意有： ‎ ‎∵ ‎ ‎∴ ‎ ‎∴‎ ‎∴‎ ‎(3)依题意有： ， ， ‎ ‎∴ ‎ ‎∴ ，∴ ‎ ‎∴‎ ‎∴‎ ‎8.如图1，在 中，， ， ，另有一直角梯形 的底边 落在 上，腰 落在 上，且 ， ， ．‎ ‎(1)延长 交 于 ，求 的面积；‎ ‎(2)操作：固定 ，将直角梯形 以每秒1个单位的速度沿 方向向右移动，直到点 与点 重合时停止，设运动的时间为 秒，运动后的直角梯形为 (如图2)．‎ 探究1：在运动过程中，四边形 能否为正方形？若能，请求出此时 的值；若不能，请说明理由；‎ 探究2：在运动过程中， 与直角梯形 重叠部分的面积为 ，求 与 的函数关系式．‎ 解析：‎ ‎(1)∵ ， ，∴．‎ 又∵ ，∴ ，∴ ‎ ‎∴，即，∴．‎ ‎∴．‎ ‎(2)‎ 探究1：能为正方形．‎ ‎ ， ，∴四边形 为平行四边形．‎ 又 ，∴四边形 为矩形．‎ 又 ‎ ‎∴当 ，即 秒时，四边形 为正方形．‎ 探究2：‎ ‎∵ ，∴ ．‎ ‎∴当 秒时，直角梯形的腰 与 重合．‎ ‎①当 时，重叠部分的面积为直角梯形 的面积，如图2． ‎ 过 作 于 ，则．‎ ‎∴，．‎ ‎∴直角梯形 的面积为．‎ ‎∴．‎ ‎②‎ 当时，重叠部分的面积为梯形 的面积-矩形的面积，如图3．‎ 即 ‎ ‎∴．‎ ‎③‎ 当时，重叠部分的面积为△PDB的面积，如图4．‎ ‎∵ ，∴ ．‎ ‎∴ ‎ 即 综合①②③，与的函数关系式如下：‎ ‎9.如图，已知直角梯形 中，，，，，动点从点出发，沿线段向点作匀速运动；动点从点出发，沿线段向点作匀速运动．过点垂直于的射线交于点，交于点、、两点同时出发，速度都为每秒1个单位长度，当点运动到点，、两点同时停止运动．设点运动的时间为秒．‎ ‎(1)求、的长(用含的代数式表示)；‎ ‎(2)当为何值时，四边形构成平行四边形？‎ ‎(3)是否存在某一时刻，使射线恰好将的面积和周长同时平分？若存在，求出此时的值；若不存在，请说明理由；‎ ‎(4)探究：为何值时，为等腰三角形？‎ 解析：(1)由题意知，四边形为矩形，∴‎ ‎∴ ‎ 在中，，∴‎ 在中，‎ ‎∴‎ ‎(2)∵ ，∴当 时，四边形构成平行四边形 ‎∴，∴‎ ‎∴当时，四边形构成平行四边形 ‎(3)若射线将的周长平分，则有 即 解得 ‎ 而 ‎∴‎ 当时， .‎ 而，∴‎ ‎∴不存在某一时刻，使射线恰好将的面积和周长同时平分 ‎(4)‎ 若为等腰三角形，则：‎ ‎①当时(如图1)，则有：‎ 即，∴‎ 解得． ‎ ‎②‎ 当时(如图2)，则有：‎ 解得 ‎ ‎③‎ 当时(如图3)，则有：‎ 在中，‎ 又 ‎∴‎ 解得， (不合题意，舍去)‎ 综上所述，当或或时，‎ 为等腰三角形．‎