2020九年级数学上册二次函数与一元二次方程
21.3 二次函数与一元二次方程
知识点 1 二次函数与一元二次方程的联系
1.抛物线y=-3x2-x+4与x轴的交点个数是( )
A.3 B.2 C.1 D.0
2.一元二次方程3x2+2x+c=0的Δ<0,则抛物线y=3x2+2x+c与x轴的交点个数为( )
A.2 B.1 C.0 D.无法确定
3.已知抛物线y=3x2-4x+n与x轴有交点,则n的取值范围是( )
A.n> B.n≥ C.n< D.n≤
4.已知方程3x2+6x+k=0的两根分别为1和-3,则抛物线y=3x2+6x+k与x轴有________个交点,其坐标分别为____________.
5.[教材习题21.3第5题变式]已知抛物线y=(k-8)x2-6x+k的顶点在x轴上,则k=________.
6.已知抛物线y=x2-5x-6与x轴交于A,B两点(点B在点A的右侧),与y轴交于点C,求△ABC的面积.
知识点 2 用图象法求一元二次方程的近似解
7.观察下表:
x
1.2
1.3
1.4
1.5
1.6
1.7
1.8
y=x2-
x-1
-0.76
-0.61
-0.44
-0.25
-0.04
0.19
0.44
结合表格,你认为一元二次方程x2-x-1=0的一个近似解是( )
A.1.2 B.1.4 C.1.6 D.1.8
8.利用函数图象求方程-x2+2x+2=0的实数根(精确到0.1),要先作函数__________________的图象,如图21-3-1所示,它与x轴的公共点的横坐标大约是-0.7,2.7,所以方程-x2+2x+2=0的实数根为x1≈________,x2≈________.
6
图21-3-1
知识点 3 二次函数与不等式
9.二次函数y=ax2+bx+c的图象如图21-3-2所示,则函数值y>0时,x的取值范围是( )
A.x<-1 B.x>3 C.-1
3
图21-3-2
10.如图21-3-3,若抛物线y1=-x2+2x+3与直线y2=ax+b(a≠0)相交于A(-,m),B(2,n)两点,当y1>y2时,x的取值范围是__________.
图21-3-3
11.[教材习题21.3第9题变式]已知函数y=x2-2x-3的图象如图21-3-4所示,利用图象法求不等式x2-2x-3<5的解集.
图21-3-4
6
12.若一元二次方程x2+px-q=0无实数根,则抛物线y=-x2-px+q位于( )
A.x轴的下方 B.x轴的上方
C.第二、三、四象限 D.第一、二、三象限
13.二次函数y=ax2+bx+c和正比例函数y=x的图象如图21-3-5所示,则方程ax2+(b-)x+c=0(a≠0)的两根和( )
A.大于0 B.等于0 C.小于0 D.不能确定
图21-3-5
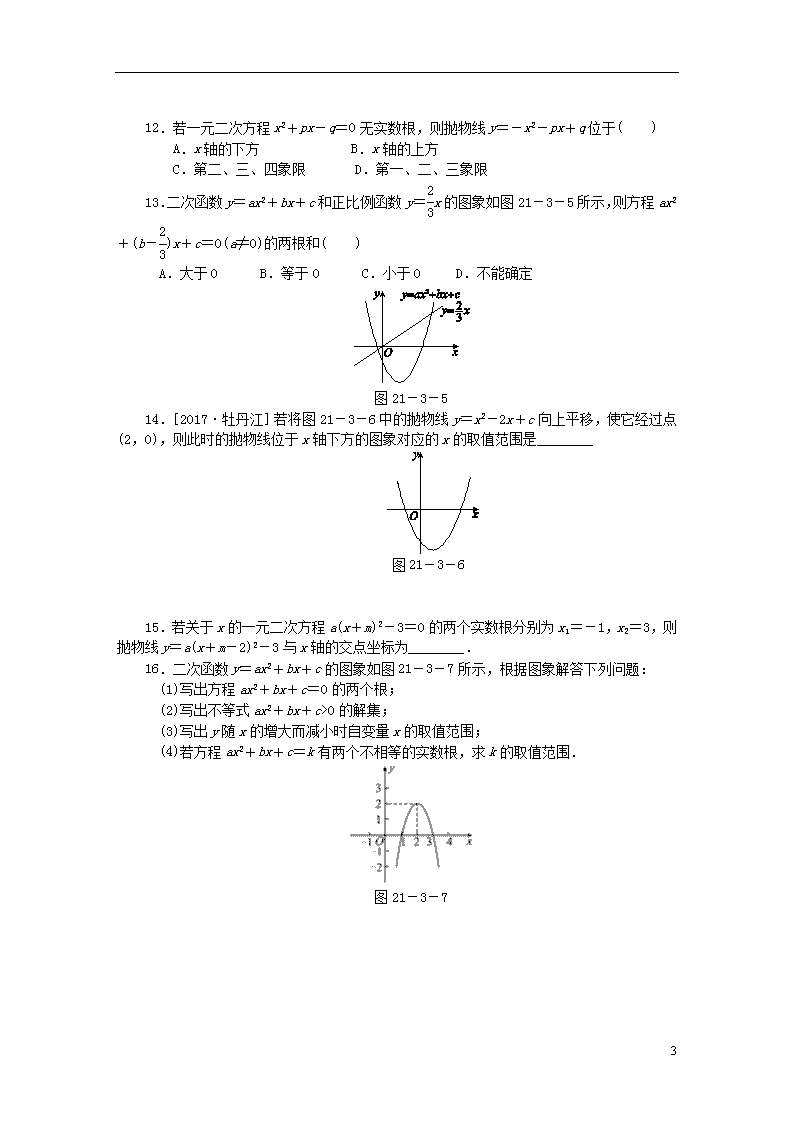
14.[2017·牡丹江]若将图21-3-6中的抛物线y=x2-2x+c向上平移,使它经过点(2,0),则此时的抛物线位于x轴下方的图象对应的x的取值范围是________
图21-3-6
15.若关于x的一元二次方程a(x+m)2-3=0的两个实数根分别为x1=-1,x2=3,则抛物线y=a(x+m-2)2-3与x轴的交点坐标为________.
16.二次函数y=ax2+bx+c的图象如图21-3-7所示,根据图象解答下列问题:
(1)写出方程ax2+bx+c=0的两个根;
(2)写出不等式ax2+bx+c>0的解集;
(3)写出y随x的增大而减小时自变量x的取值范围;
(4)若方程ax2+bx+c=k有两个不相等的实数根,求k的取值范围.
图21-3-7
6
17.已知抛物线y=x2-2(m+1)x+2(m-1).
(1)求证:不论m取何值,抛物线必与x轴相交于两点;
(2)试探究:不论m取何值,抛物线必经过一个定点.
18.阅读下面的材料:
上课时李老师提出一个问题:对于任意实数x,关于x的不等式x2-2x-1-a>0恒成立,求a的取值范围.
小捷的思路是原不等式等价于x2-2x-1>a,设函数y1=x2-2x-1,y2=a,画出两个函数的图象的示意图,于是原问题转化为函数y1的图象在y2的图象上方时a的取值范围.
(1)请结合小捷的思路回答:
对于任意实数x,关于x的不等式x2-2x-1-a>0恒成立,则a的取值范围是________.
(2)参考小捷思考问题的方法,解决问题:
关于x的方程x-4=在0<x<4范围内有两个解,求a的取值范围.
6
图21-3-8
1.B [解析] 抛物线与x轴的交点坐标分别为(-,0),(1,0),也可用判别式判断方程-3x2-x+4=0有两个不相等的实数根.总之,抛物线与x轴的交点个数为2.
2.C
3.D [解析] 抛物线y=3x2-4x+n与x轴有交点,则Δ≥0,即16-12n≥0,∴n≤.故选D.
4.两 (1,0),(-3,0) [解析] 方法一:利用方程的根,把x=1代入求出k=-9,然后求抛物线与x轴的交点.方法二:直接根据二次函数与x轴的交点情况与对应的一元二次方程之间的关系,直接得出两个交点的坐标为(1,0),(-3,0).
5.9或-1 [解析] 抛物线的顶点在x轴上,则Δ=0,∴62-4k(k-8)=0,解得k1=9,k2=-1.故答案为9或-1.
6.[解析] 欲求△ABC的面积,必须先求出A,B,C三点的坐标.
解:令y=0,得一元二次方程x2-5x-6=0,解方程,得x1=6,x2=-1,
∴抛物线y=x2-5x-6与x轴的交点B,A的坐标分别为(6,0),(-1,0).
把x=0代入y=x2-5x-6,得y=-6,
∴点C的坐标为(0,-6).
∴S△ABC=AB·OC=(6+1)×6×=21.
7.C 8.y=-x2+2x+2 -0.7 2.7
9.D 10.-<x<2
11.解:如图,在平面直角坐标系中作出直线y=5,观察直线y=5与抛物线y=x2-2x-3的两个交点坐标为(-2,5)和(4,5),在直线y=5的下方,y=x2-2x-3的函数值都小于5,故不等式x2-2x-3<5的解集为-2<x<4.
12.A
[解析] ∵a=-1<0,∴抛物线开口向下.∵一元二次方程x2+px-q=0无实数根,∴函数y=-x2-px+q的图象与x轴无交点,∴抛物线y=-x2-px+q位于x轴的下方.故选A.
6
13.A [解析] 方程ax2+(b-)x+c=0可转化为ax2+bx+c=x,得到二次函数与正比例函数图象的两个交点的横坐标即为该方程的两根.不妨设这两根分别为x1,x2且x10的解集为1
查看更多