- 2021-11-11 发布 |
- 37.5 KB |
- 11页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
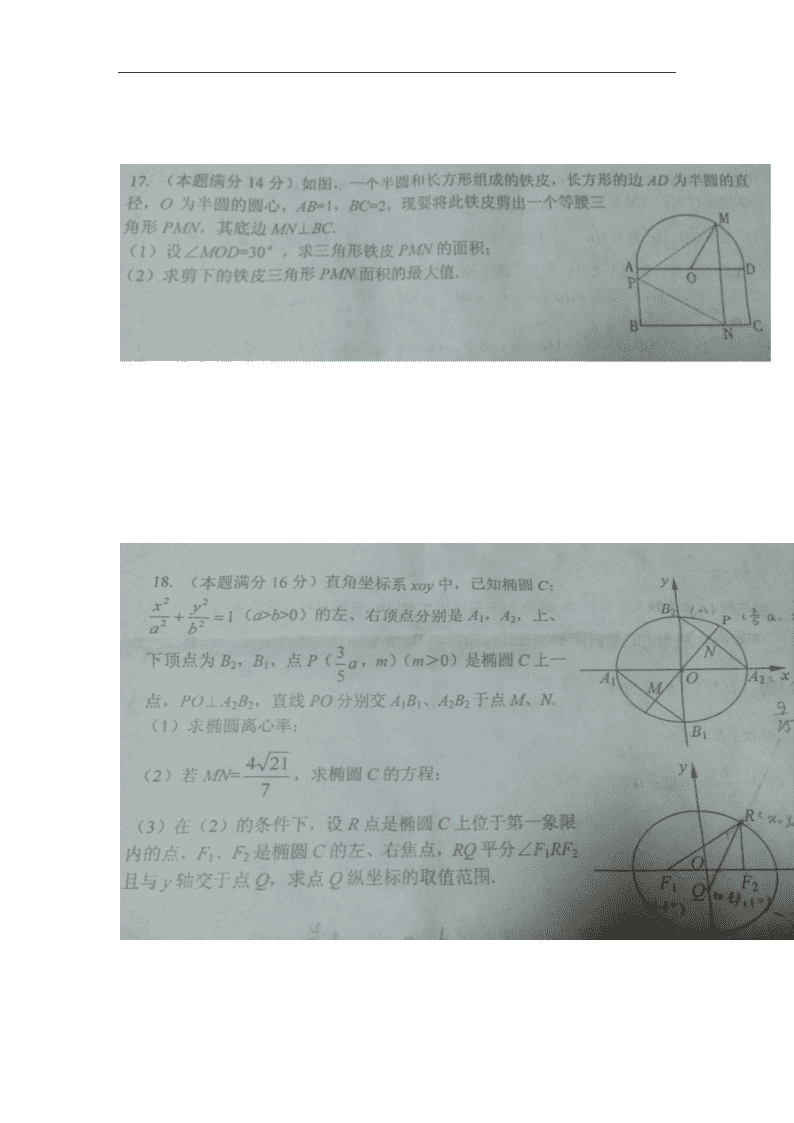
江苏省泰州市2012-2013学年度第一学期期末考试高三数学试题
泰州市2012-2013学年度第一学期期末考试 高三数学试题 命题人:朱占奎 杨鹤云 肖彬 审题人:孟泰 石志群 一、 填空题 1. 已知集合,,则= 2. 设复数,,则= 3. 若数据,3的平均数是3,则数据的平均数是 4. 设双曲线的左、右焦点分别为,,点P为双曲线上位于第一象限内一点,且的面积为6,则点P的坐标为 5.曲线y=2lnx在点(e,2)处的切线与y轴交点的坐标为 6.如图,ABCD是45的方格纸,向此四边形ABCD内抛撒一粒豆子,则豆子恰好落在阴影部分内的概率为 7.设函数f(x)是定义在R上的奇函数,且f(a)>f(b), 则f(-a) f(-b)(填“>”或:“<”) 8.在空间中,用a,b,c表示三条不同的直线,表示平面,给出下列四个命题: (1)若,则(2)若,则 (3) 若,,则(4)若,,则 9.右图是一个算法流程图,则输出p= 10.已知点P(t,2t)( )是圆C:内一点,直线 tx+2ty=m圆C相切,则直线x+y+m=0与圆C的关系是 11.设a,s: 数列是递增数列;t:a,则s是t的 条件 12.各项均为正数的等比数列中,若,,,则的取值范围是 13.已知六个点,,,,, (,)都在函数f(x)=sin(x+)的图象C上,如果这六个点中不同两点的连线的中点仍在曲线C上,则称此两点为“好点组”,则上述六点中好点组的个数为 (两点不计顺序) 14.已知f(x)= ,.若,则的取值范围是 二.解答题 15.已知向量a=(cos,cos(),b=(,sin), (1)求的值 (2)若,求 (3),求证: 16.在三棱锥S-ABC中,SA平面ABC,SA=AB=AC=,点D是BC边的中点,点E是线段AD上一点,且AE=4DE,点M是线段SD上一点, (1)求证:BCAM (2)若AM平面SBC,求证:EM平面ABS 19.(本题满分16分)已知数列,,其中 (1)求满足=的所有正整数n的集合 (2)n16,求数列的最大值和最小值 (3)记数列的前 n项和为,求所有满足(m查看更多