中考数学复习冲刺专项训练精讲：三角形全等教学课件（初三数学章节复习课件）

中考数学复习冲刺专项训练精讲：三角形全等教学课件（初三数学章节复习课件）

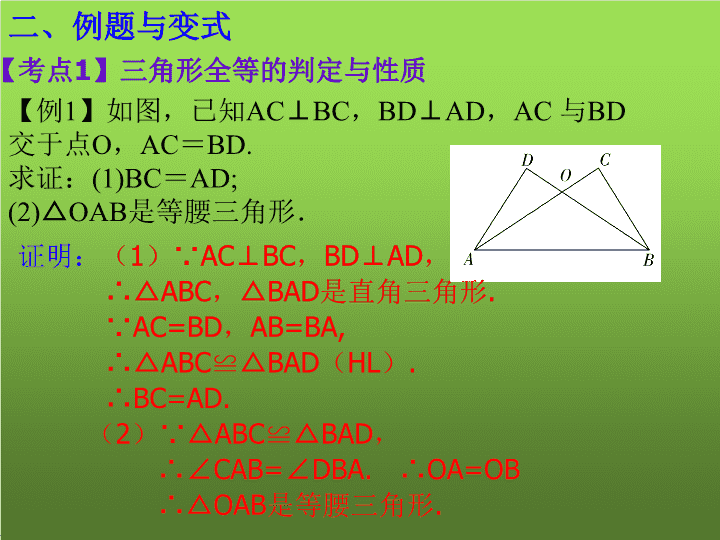
第四章 三角形 三角形全等 中考数学复习冲刺专项训练精讲 1．三角形全等的判定方法有：__________、 __________、__________、__________，直角三角形 全等的判定除以上的方法外还有__________． 一、考点知识 ， 2．全等三角形的性质：对应边__________，对应角 __________，周长________，面积__________． SSS AASASASAS HL 相等 相等 相等相等 【例1】如图，已知AC⊥BC，BD⊥AD，AC 与BD 交于点O，AC＝BD. 求证：(1)BC＝AD; (2)△OAB是等腰三角形． 【考点1】三角形全等的判定与性质 二、例题与变式 证明：（1）∵AC⊥BC，BD⊥AD， ∴△ABC，△BAD是直角三角形. ∵AC=BD，AB=BA, ∴△ABC≌△BAD（HL）. ∴BC=AD. （2）∵△ABC≌△BAD， ∴∠CAB=∠DBA. ∴OA=OB ∴△OAB是等腰三角形. 【变式1】如图，在正方形ABCD中，E，F分别是AB， BC上的点，且AE＝BF.求证：CE＝DF. 证明：在正方形ABCD中，AB=BC=CD， ∠B=∠BCD=90°，∵AE=BF， ∴AB－AE=BC－BF，即BE=CF. 在△BCE和△CDF中，BC＝CD， ∠B＝∠FCD＝90°，BE＝CF， ∴△BCE≌△CDF（SAS）. ∴CE=DF. 【考点2】三角形全等的判定与性质 【例2】如图，BD是菱形ABCD的对角线，点E，F分别在 边CD，DA上，且∠DFB＝∠DEB. 求证：CE＝AF. 证明：∵BD是菱形ABCD的对角线， ∴∠ADB=∠CDB，AD=CD. 又∵∠DFB=∠DEB, BD=BD, ∴△DFB≌△DEB. ∴DF=DE. ∴AD－DF=CD－DE. ∴CE=AF. 【变式2】如图，已知菱形ABCD中，E，F分别是 CB，CD上的点，且BE＝DF. 求证：(1)△ABE≌△ADF； (2)∠AEF＝∠AFE. 证明：（1）∵四边形ABCD是菱形， ∴AB=AD，∠B=∠D. 又∵BE=DF， ∴△ABE≌△ADF. （2）∵△ABE≌△ADF， ∴AE=AF. ∴∠AEF=∠AFE. 【考点3】三角形全等的判定与性质 【例3】如图，在Rt△ABC中，∠ACB＝90°，AC＝BC， 点D为AB边上一点，且不与A，B两点重合，AE⊥AB， AE＝BD，连接DE，DC. (1)求证：△ACE≌△BCD； (2)求证：△DCE是等腰直角三角形． 证明：如图，（1）∵∠ACB=90°，AC=BC， ∴∠B=∠2=45°. ∵AE⊥AB，∴∠1+∠2=90°． ∴∠1=45°．∴∠1=∠B． 在△ACE和△BCD中，AE＝BD，∠1＝∠B，AC＝BC， ∴△ACE≌△BCD（SAS）. （2）∵△ACE≌△BCD，∴CE=CD，∠3=∠4． ∵∠4+∠5=90°，∴∠3+∠5=90°.即∠ECD=90°. ∴△DCE是等腰直角三角形. 【变式3】如图，△ABC和△ADE都是等腰直角三角形， ∠BAC＝∠DAE＝90°，四边形ACDE是平行四边形，连 接CE交AD于点F，连接BD交CE于点G，连接BE. 求证：(1)CE＝BD； (2)∠ADB＝∠AEB . 证明：（1）∵∠BAC=∠DAE=90°， ∴∠BAC+∠DAC=∠DAE+∠DAC， 即∠BAD=∠CAE. ∵△ABC和△ADE都是等腰直角三角形， ∴AB=AC，AE=AD， ∴△BAD≌△CAE（SAS）. ∴CE=BD. （2）∵四边形ACDE是平行四边形， ∴AE∥CD. ∴∠ADC=∠DAE=90°，AE=CD， ∵△ADE是等腰直角三角形，∴AE=AD. ∴AD=CD. ∴△ADC是等腰直角三角形. ∴∠CAD=45°. ∴∠BAD=90°+45°=135°. ∵∠DAE=∠BAC=90°，∠CAD=45°， ∴∠BAE=360°－90°－90°－45°=135°. 又∵AB=AB，AD=AE，∴△BAE≌△BAD（SAS）， ∴∠ADB=∠AEB. A组 1．如图，在四边形ABCD中，AB＝AD， CB＝CD，若连接AC，BD相交于点O，则 图中全等三角形共有________对． 三、过关训练 2．已知：如图，点C为AB中点，CD＝BE，CD∥BE. 求证：△ACD≌△CBE. 3 证明：∵C是AB的中点（已知），∴AC=CB． ∵CD∥BE（已知），∴∠ACD=∠B． 在△ACD和△CBE中，AC＝CB, ∠ACD＝∠CBE , CD＝BE , ∴△ACD≌△CBE（SAS）. 3．如图，点A，B，C，D在一条直线上，AB＝CD， AE∥BF，CE∥DF. 求证：AE＝BF. 证明：∵AE∥BF， ∴∠A=∠FBD. ∵CE∥DF， ∴∠D=∠ACE. ∵AB=CD，∴AB+BC=CD+BC，即AC=BD. 在△ACE和△BDF中， ∠A=∠FBD, AC=BD，∠D=∠ACE， ∴△ACE≌△BDF（ASA）. ∴AE=BF． B组 4．如图，▱ ABCD的对角线AC，BD相交于点O， EF过点O且与AB，CD分别相交于点E，F. 求证：△AOE≌△COF. 证明：∵四边形ABCD是平行四边形， ∴OA=OC，AB∥CD. ∴∠EAO=∠FCO. 在△AOE和△COF中， ∠EAO＝∠FCO. AO＝CO，∠EOA＝∠FOC， ∴△AOE≌△COF（ASA） 5．如图，在△ABC中，∠ACB＝90°， AC＝BC，BE⊥CE 于点E，AD⊥CE于点D. 求证：△BEC≌△CDA. 证明：∵BE⊥CE于点E, AD⊥CE于点D, ∴∠BEC=∠CDA=90°. 在Rt△BEC中,∠BCE+∠CBE=90°, 在Rt△BCA中,∠BCE+∠ACD=90°. ∴∠CBE=∠ACD. 在△BEC和△CDA中,∠BEC=∠CDA, ∠CBE=∠ACD, BC=AC, ∴△BEC≌△CDA（AAS） 6．如图，在菱形ABCD中，E，F分别是CB，CD 上的点，且BE＝DF，求证：EF⊥AC . 证明：分别连接AE,AF， ∵菱形ABCD， ∴AB=AD=BC=CD，∠B=∠D， 又∵BE=DF，∴△ABE≌△ADF. ∴AE=AF.∴点A在EF的垂直平分线上， ∵BE=DF，BC=CD，∴CE=CF. ∴点C在EF的垂直平分线上，∴EF⊥AC C组 7．如图1，等边三角形ABC中，D是AB上一点，以CD为边 向上作等边三角形CDE，连接AE. (1)求证：AE∥BC; (2)如图2，若点D在AB的延长线上，其余条件均不变， (1)中结论是否成立？请说明理由． 证明：（1）∵△ABC和△DCE是等边三角形， ∴BC=AC，DC=EC，∠BCA=∠DCE=∠B=∠BAC=60°， ∴∠BCA－∠ACD=∠DCE－∠ACD，即∠BCD=∠ACE. ∴△BCD≌△ACE（SAS）. ∴∠B=∠CAE，∴∠B=∠CAE=∠BAC=60°. ∴∠CAE+∠BAC=∠BAE=120°. ∴∠B+∠BAE=180°. ∴AE∥BC. （2）成立，证明如下： 由（1）,得 ∵△DBC≌△AEC，∴∠DBC=∠EAC. ∵△ABC是等边三角形，∴∠ABC =∠BAC=60°. ∴∠DBC= 180°－60°=120°. ∴∠EAC=∠DBC=120°. ∴∠EAD=∠EAC－∠BAC=60°. ∴∠EAD =∠ABC=60°. ∴AE∥BC. (2)如图2，若点D在AB的延长线上，其余条件均不变， (1)中结论是否成立？请说明理由．