中考数学复习冲刺专项训练精讲：几种重要的线段教学课件（初三数学章节复习课件）

中考数学复习冲刺专项训练精讲：几种重要的线段教学课件（初三数学章节复习课件）

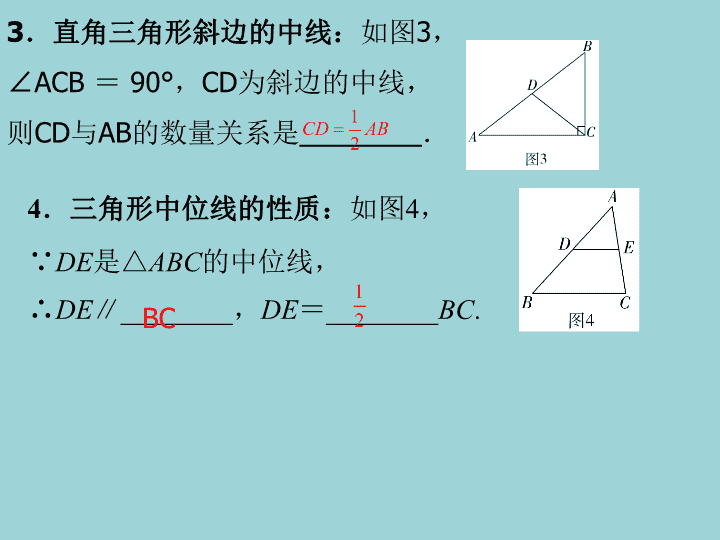
第四章 三角形 几种重要的线(段) 中考数学复习冲刺专项训练精讲 1．角平分线：如图1， (1)∵OC是∠AOB的平分线，PD⊥OA，PE⊥OB， ∴PD＝__________． (2)∵PD＝__________，PD⊥OA，PE⊥OB， ∴点P在∠AOB的平分线上． 一、考点知识 ， 2．线段的垂直平分线：如图2， (1)∵直线PO是线段AB的垂直平分线， ∴PA＝________． (2)∵PA＝________， ∴点P在线段AB的垂直平分线上． PE PE PB PB 3．直角三角形斜边的中线：如图3， ∠ACB ＝ 90°，CD为斜边的中线， 则CD与AB的数量关系是________． 4．三角形中位线的性质：如图4， ∵DE是△ABC的中位线， ∴DE∥________，DE＝________BC.BC 1 2 CD AB 1 2 【例1】如图，在Rt△ABC中，∠ACB ＝ 90°，D， E，F分别是AB，BC，CA的中点，若CD ＝ 5cm， 求EF的长． 【考点1】中位线的性质，直角三角形斜边的中线 二、例题与变式 解：∵CD是Rt△ABC斜边上的中线，CD = 5 cm， ∴AB=2CD=10 cm. ∵E，F分别是BC，CA的中点， ∴EF= AB=5.1 2 【变式1】如图，在Rt△ABC中，∠BAC＝90°， D，E分别是AB，BC的中点，F在CA的延长线上， ∠FDA＝∠B，AC＝6，AB＝8，求四边形AEDF的 周长． 解：在Rt△ABC中，AC=6，AB=8， 根据勾股定理求出BC=10. 再根据三角形中位线定理和直角三角形斜边上的中线性质 求出DE= AC=3和AE= BC=5. 由已知可判定四边形AEDF是平行四边形， 从而求得四边形AEDF的周长=2×（3+5）=16. 1 2 1 2 【考点2】角平分线的性质 【例2】如图，Rt△ABC中，∠C＝90°，AD平分 ∠CAB，DE⊥AB于点E,若AC＝6，BC＝8，CD＝3. (1)求DE的长； (2)求△ADB的面积． 解：（1）∵AD平分∠CAB，DE⊥AB， ∠C=90°，∴CD=DE. ∵CD=3， ∴DE=3. （2）在Rt△ABC中，由勾股定理, 得AB= . ∴△ADB的面积为S= AB×DE= ×10×3=15. 2 2 2 26 8 10AC BC    1 2 1 2 【变式2】如图，在△ABC中，CD是AB边上的高， BE平分∠ABC，交CD于点E，BC＝5，DE＝2，求 △BCE的面积． 解：过点E作EF⊥BC交BC于点F, 根据角平分线的性质可得DE=EF=2. 所以△BCE的面积等于 ×BC×EF= ×5×2=5. 1 2 1 2 【考点3】直角三角形斜边的中线，垂直平分线 【例3】如图，在△ABC中，点D在AB上，且CD＝CB，点 E为BD的中点，点F为AC的中点，连接EF交CD于点M，连接 AM. (1)求证：EF＝ AC. (2)若∠BAC＝45°，求线段AM，DM，BC之间的数量关系． 解：（1）证明：∵CD=CB，点E为BD的中点， ∴CE⊥BD，∠AEC=90°. 又∵点F为AC的中点，∴EF= AC. （2）解：∵∠BAC=45°，CE⊥BD， ∴△AEC是等腰直角三角形. ∵点F为AC的中点，∴EF垂直平分AC，∴AM=CM. ∵CD=CM+DM=AM+DM，CD=CB，∴BC=AM+DM. 1 2 1 2 【变式3】如图，在△ABC中，∠ABC＝45°，CD⊥AB 于点D，BE⊥AC于点E，且BE平分∠ABC，F为BC中点， BE与DF，CD分别交于点G，H. 求证：(1)BH＝AC； (2)BG2－ GE2＝EA2. 证明： (1)∵CD⊥AB，∴∠BDC=∠CDA=90°. ∵∠ABC=45°，∴∠BCD=∠ABC=45°.∴BD=CD， ∵∠ABE+∠A =∠ACD+∠A =90°，∴∠ABE=∠ACD. ∴△DBH≌ △DCA. ∴BH=AC. （2）连接GC，在Rt△CGE中，∴CG2－ GE2 =EC2， ∵F为BC中点，BD=CD，∴DF垂直平分BC.∴BG=CG. 由BE平分∠ABC，BE⊥AC ，易证EC=EA， ∴BG2－ GE2 =EA2. A组 1．如图，等腰三角形ABC的周长为21，底边BC＝5， AB的垂直平分线DE交AB于点D，交AC于点E，则 △BEC的周长为________． 三、过关训练 3．如图，在四边形ABCD中，E，F，G，H分别是边 AB，BC，CD，DA的中点，依次连接各边中点得到中 点四边形EFGH. (1)这个中点四边形EFGH的形状是__________； (2)请证明(1)的结论． 2．如图，∠ABC＝50°，AD垂直平分线段BC于点D， ∠ABC的平分线BE交AD于点E，连接EC，则∠AEC的 度数是__________． 13 115° 平行四边形 证明：连接AC，∵E是AB的中点，F是BC的中点， ∴EF∥AC，EF= AC，同理HG∥AC，HG= AC. 综上所述，EF∥HG.故四边形EFGH是平行四边形. 1 2 1 2 B组 4．如图：已知△ABC中，AB＝AC，∠A＝36°， AC的垂直平分线交AB点于点E，点D为垂足，连接 EC. (1)求∠ECD的度数； (2)若CE＝8，求BC长． 解：（1）∵DE是AC的垂直平分线， ∴EC=EA，∴∠ECD=∠A=36°. （2）∵AB=AC，∴∠B=∠ACB= (180°－36°)=72°， ∵∠BEC是△AEC的外角，∴∠BEC=36°+36°=72°. ∴∠BEC=∠B. ∴BC=CE=8. 1 2 5．已知正方形ABCD中，E为对角线BD上一点， 过E点作EF⊥BD交BC于点F，连接DF，G为DF中点， 连接EG，CG.求证：EG＝CG. 证明：∵EF⊥BD，∴△DEF为直角三角形. ∵G为DF中点，∴EG= DF， （直角三角形斜边上的中线等于斜边的一半）， 在正方形ABCD中，∠BCD=90°， 又G为DF中点， ∴CG= DF. ∴EG=CG. 1 2 1 2 6．如图，在△ABC中，AD平分∠BAC，BD⊥AD， 垂足为点D，过点D作DE∥AC，交AB于点E，若AB ＝5，求线段DE的长． 解：∵AD平分∠BAC，∴∠BAD＝∠CAD. ∵DE∥AC，∴∠CAD＝∠ADE. ∴∠BAD＝∠ADE.∴AE＝DE. ∵AD⊥DB，∴∠ADB＝90°.∴∠BAD＋∠ABD＝90°. ∵∠ADE＋∠BDE＝∠ADB＝90°.∴∠ABD＝∠BDE. ∴DE＝BE， ∵AB＝5，∴DE＝BE＝AE＝ AB＝2.5.1 2