九年级下册数学人教版课件28-1 锐角三角函数（第2课时）

九年级下册数学人教版课件28-1 锐角三角函数（第2课时）

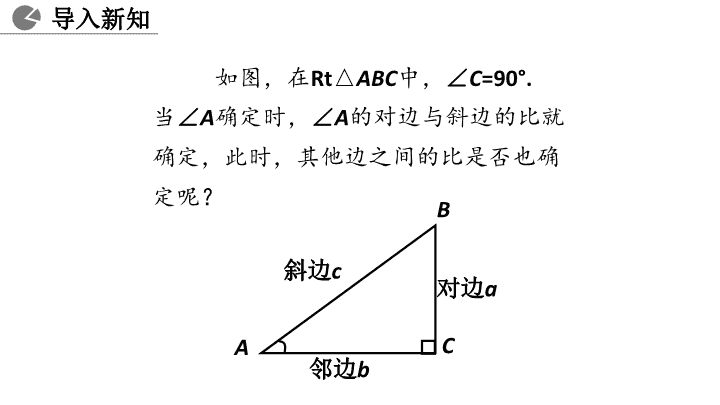
人教版 数学 九年级 下册 如图，在Rt△ABC中，∠C=90°. A C B 对边a 邻边b 斜边c 当∠A确定时，∠A的对边与斜边的比就 确定，此时，其他边之间的比是否也确 定呢？ 导入新知 2. 能灵活运用锐角三角函数进行相关运算. 1. 通过类比正弦函数，理解余弦函数、正切函 数的定义，进而得到锐角三角函数的概念 . 素养目标 3. 通过锐角三角函数的学习，培养学生类比 学习的能力. 如图， △ABC 和 △DEF 都是直角三角形， 其中∠A =∠D，∠C =∠F = 90°，则 成立吗？为什么？ DE DF AB AC  A B C D E F 探究新知 知识点 1 余弦的定义 我们来试着证明前面的问题： ∵∠A=∠D，∠C=∠F=90°， ∴ ∠B=∠E. 从而 sinB = sinE， 因此 .AC DF AB DE  A B C D E F 探究新知 在有一个锐角相等的所有直角三角形中，这个锐 角的邻边与斜边的比值是一个常数，与直角三角形的 大小无关． 如下图所示，在直角三角形中，我们把锐角A的邻 边与斜边的比叫做∠A的余弦，记作cosA，即 归纳： A B C 斜边c 邻边b 探究新知 ∠A的邻边 斜边 cos A = b c  探究新知 归纳总结 从上述探究和证明过程，可以得到互余两角的三 角函数之间的关系： 对于任意锐角α，有 cos α = sin (90°－ α), 或sin α = cos(90°－ α). 1. sinA、cosA是在直角三角形中定义的，∠A是锐角(注 意数形结合，构造直角三角形). 2. sinA、 cosA是一个比值（数值）. 3. sinA、 cosA的大小只与∠A的大小有关，而与直角三 角形的边长无关. 如图：在Rt △ABC中，∠C＝90°， 正弦: 余弦: sin 的对边 = 斜边 A aA c   cos 的邻边 = 斜边 A bA c   探究新知 注意： A B C 斜边c ∠A的邻边b ∠A的对边a Rt△ABC中，∠C=90°，如果AB=2，BC=1，那么 cosB的值为（ ） A. B. C. D. 2 3 3 3 3 2 1 A 巩固练习 Rt△ABC中，∠C=90°，如果AC=4，BC=3， 那么cosB的值为_______. 3 5 如图， △ABC 和 △DEF 都是直角三角形， 其中∠A =∠D，∠C =∠F = 90°，则 成立吗？为什么？ DF EF AC BC  A B C D E F 探究新知 知识点 2 正切的定义 证明：∵∠C=∠F=90°， ∠A=∠D， ∴Rt△ABC ∽ Rt△DEF. 探究新知 A B C D E F ， DF AC EF BC ∴ 即 . DF EF AC BC  当直角三角形的一个 锐角的大小确定时，其 对边与邻边比值也是唯 一确定的吗？ 探究新知 A B C 斜边c ∠A的邻边b ∠A的对边a 如图：在Rt △ABC中，∠C＝90°， 我们把锐角A的对边与邻边的比叫做 ∠A的 正切，记作 tanA. 探究新知 在直角三角形中，当锐角A的度数一定时，不管三角 形的大小如何，∠A的对边与邻边的比是一个固定值. A B C 斜边c ∠A的邻边b ∠A的对边a 1.如果两个角互余，那么这两个角的正切值有什么关系？ 【想一想】 探究新知 2.锐角A的正切值可以等于1吗？为什么？ 可以大于1吗？ 5 3 4 5 4 3 3 4A. B. C. D. 在Rt∆ABC中，∠C＝90°，如果 那么tanB的值为（ ）D 巩固练习 ， 5 4cos A 在Rt∆ABC中，∠C＝90°，如果 那么tanA的值为_______. ， 13 5sin A 5 12 锐角A的正弦、余弦、和正切统称∠A的锐角三角函数. sin A= cos A= tan A= 脑中有“图”，心中有 “式” 探究新知 知识点 3 锐角三角函数的定义 A B C 斜边c ∠A的邻边b ∠A的对边a ∠A的邻边 斜边 ∠A的对边 斜边 ∠A的对边 ∠A的邻边 例1 如图，在 Rt△ABC 中，∠C=90°，AB=10， BC=6，求sinA，cosA，tanA的值. A B C 10 6 解：由勾股定理,得 2 2 2 2 = = 10 6 =8AC AB BC  ， 因此 6 3sin = = 10 5 BCA AB  ， 6 3tan = = . 8 4 BCA AC  探究新知 素养考点 1 已知直角三角形两边求锐角三角函数的值 8 4cos 10 5 ACA AB ,   探究新知 方法点拨 已知直角三角形中的两条边求锐角三角函数值的一 般思路是：当所涉及的边是已知时，直接利用定义求锐 角三角函数值；当所涉及的边是未知时，可考虑运用勾 股定理的知识求得边的长度，然后根据定义求锐角三角 函数值． α A Rt△ABC中，∠C为直角，AC=5，BC=12，那么下列∠A 的四个三角函数中正确的是( ) 如图：P是∠ α的边OA上一点，且 P点的坐标为（3，4），则cosα ______，tan α= ________. B 3 5 4 3 巩固练习 A. B． 13 5sin A 13 12sin A C． D． 12 13tan A 12 5cos A A B C 6 又 2 2 2 210 6 8AC AB BC     ， 在直角三角形中， 如果已知一边长及一个 锐角的某个三角函数值， 即可求出其它的所有锐 角三角函数值. 探究新知 素养考点 2 已知一边及一锐角三角函数值求函数值 例2 如图，在 Rt△ABC中，∠C = 90°，BC = 6， ，求 cosA , tanB 的值． 3sin 5 A  4cos 5 ACA AB  = ，∴ 4tan . 3 ACB BC  = 解：∵在Rt△ABC中， sin BCA AB  ， 56 10 sin 3 BCAB A  = = .∴ A B C 8 解：∵在 Rt△ABC中， 3tan 4 BCA AC   ， 6 3cos . 10 5 BCB AB    3 3 8 6 4 4 BC AC    ，∴ 2 2 2 28 6 10AB AC BC     ，∴ 6 3sin 10 5 BCA AB    ，∴ 巩固练习 如图，在 Rt△ABC 中，∠C = 90°，AC = 8， ，求sinA， cosB 的值． 3tan 4 A  1. 如图，旗杆高AB=8m，某一时刻，旗杆影子长BC=16m，则 tanC=______． 连接中考 1 2 A BC B 连接中考 2. 如图，A , B , C是小正方形的顶点，且每个小正方形的 边长为1，则tan∠BAC的值为（　　） A． B．1 C． D． 2 1 3 3 3 1. 在Rt△ABC中，∠C = 90°，AC = 12，AB =13. sinA=______，cosA=______，tanA=____， sinB=______，cosB=______，tanB=____. 5 13 12 13 5 12 5 13 12 13 12 5 基 础 巩 固 题 课堂检测 2. 如图，△ABC 中一边 BC 与以 AC 为直径的 ⊙ O相 切与点 C，若 BC=4，AB=5，则 tanA=___. 4 3 A B C 课堂检测 O 3. 已知 ∠A，∠B 为锐角， (1) 若∠A =∠B，则 cosA cosB; (2) 若 tanA = tanB，则∠A ∠B; (3) 若 tanA · tanB = 1，则 ∠A 与 ∠B 的关系为： . = = ∠A +∠B = 90° 课堂检测 如图，在 Rt△ABC 中，∠ACB = 90°，CD⊥AB，垂足 为 D. 若 AD = 6，CD = 8. 求 tanB 的值. 解: ∵ ∠ACB＝∠ADC =90°， ∴∠B+ ∠A=90°, ∠ACD+ ∠A =90°. ∴∠B = ∠ACD. 能 力 提 升 题 6 3tan tan . 8 4     ADB ACD CD ∴ 课堂检测 如图，在△ABC中，AB=AC=4，BC=6. 求cosB 及 tanB 的值. 解：过点 A 作 AD⊥BC 于 D. ∵ AB = AC， ∴ BD = CD = 3， 在 Rt△ABD 中, 2 2 2 24 3 7AD AB BD     ， A B CD 提示：求锐角的三角函数值问题，当图形 中没有直角三角形时，可用恰当的方法构 造直角三角形. 拓 广 探 索 题 ∴ 3cos . 4 BDB AB   ∴ 7tan . 3   ADB BD 课堂检测 余弦函数 和 正切函数 余弦 正切 性质 课堂小结 ∠A的邻边 斜边cos A = ∠A的对边tan A =∠A的邻边 ∠A的大小确定的情况下， cosA，tanA为定值，与三 角形的大小无关 课后作业 作业 内容 教 材 作 业 从课后习题中选取 自 主 安 排 配套练习册练习