苏教版数学九年级上册教案2-3确定圆的条件

苏教版数学九年级上册教案2-3确定圆的条件

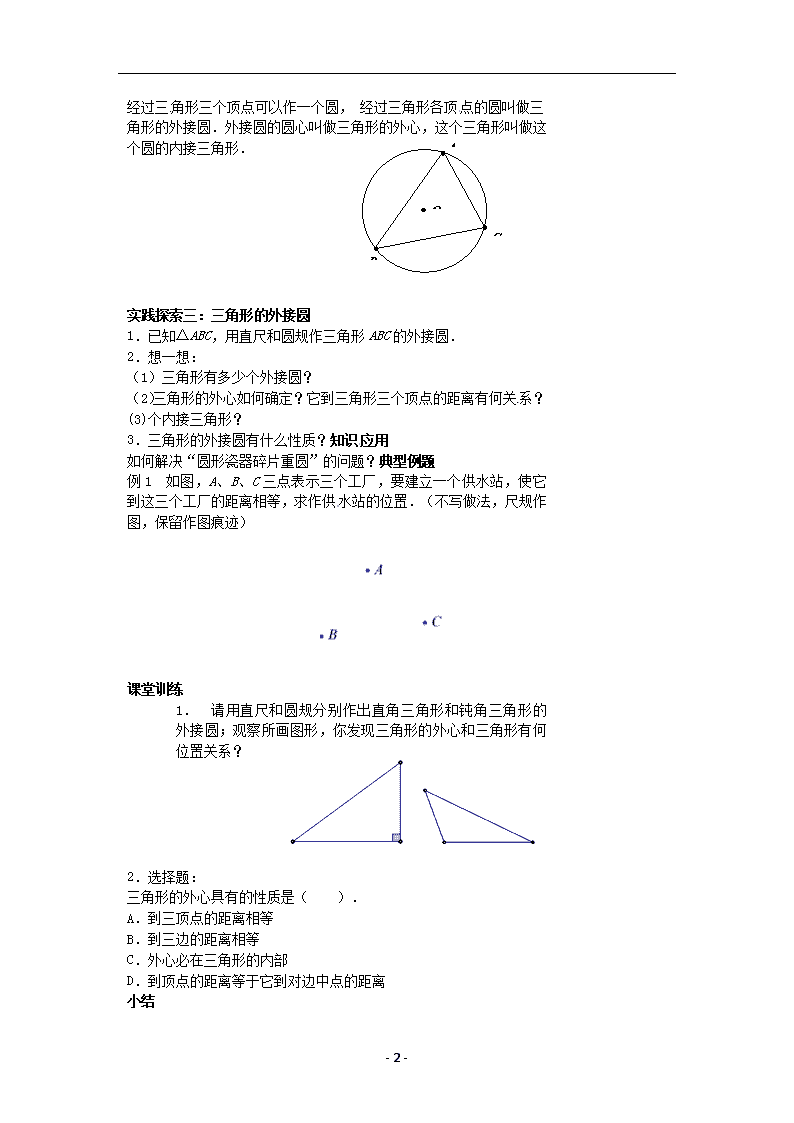
- 1 - 2.3 确定圆的条件 教学目标 【知识与能力】 解不在一条直线上的三点确定一个圆，了解三角形的外接圆、三角形的外心、圆的内接三角 形的概念，会过不在一条直线上的三点作圆. 能够利用尺规，过不在同一直线上的三点画出 一个圆 【过程与方法】 经历不在一条直线上的三点确定一个圆的探索过程 【情感态度价值观】 在探究过程中培养学生归纳探索的精神，渗透类比化归的思想. 教学重难点 【教学重点】 了解不在一条直线上的三点确定一个圆. 【教学难点】 通过类比，经历确定圆的 条件的探索过程，说明过不在同一直线上的三点有且只有 一个圆. 课前准备 无 教学过程 情境引入 考古学家在长沙马王堆汉墓挖掘时，发现一圆形瓷器碎片，你能帮助 考古学家画出这个碎片所在的整圆，以便于进行深入的研究吗？ 复习回顾 （1）过一点可作几条直线？ （2）过几点可确定一条直线？ （3）过几个点可以确定一个圆呢？ 实践探索一：确定圆的条件 1．经过已知点 A 作圆，可以作多少个？ （师：请你动手画出猜想）2．经过已知点 A、B 作圆，可以作多少个？ 圆心在什么图形上？ （师：请你动手画出的猜想，你有什么发现？）3．经过 A、B、C 三 点，能不能作圆？如果能，可以作多少个？圆心在什么位置？如果不 能，请说明理由． （教师进行分步引导： A、B、C 三点有怎样的位置关系？ ①如果过三个点，圆心与这三个点有什么关系？ ②经过 A、B 的圆心有什么特征？经过 B、C 的圆心有什么特征？ ③请你动手画画，你有什么发现？） 4．定理：不在同一直线上的三点确定一个圆． 实践探索二：相关概念 由定理可知： - 2 - 经过三角形三个顶点可以作一个圆， 经过三角形各顶点的圆叫做三 角形的外接圆．外接圆的圆心叫做三角形的外心，这个三角形叫做这 个圆的内接三角形． 实践探索三：三角形的外接圆 1．已知△ABC，用直尺和圆规作三角形 ABC 的外接圆． 2．想一想： （1）三角形有多少个外接圆？ （2）三角形的外心如何确定？它到三角形三个顶点的距离有何关 系？ (3)个内接三角形？ 3．三角形的外接圆有什么性质？知识应用 如何解决“圆形瓷器碎片重圆”的问题？典型例题 例 1 如图，A、B、C 三点表示三个工厂，要建立一个供水站，使它 到这三个工厂的距离相等，求作供水站的位置．（不写做法，尺规作 图，保留作图痕迹） 课堂训练 1． 请用直尺和圆规分别作出直角三角形和钝角三角形的 外接圆；观察所画图形，你发现三角形的外心和三角形有何 位置关系？ 2．选择题： 三角形的外心具有的性质是（ ）． A．到三顶点的距离相等 B．到三边的距离相等 C．外心必在三角形的内部 D．到顶点的距离等于它到对边中点的距离 O A B C - 3 - 小结 1．作直线． 过一点-------可以作无数条直线． 过两个点-----确定一条直线． 2．作圆． 过一个点——可以作无数个圆． 过两个点——可以作无数个圆． 过三个点——不在同一直线上的三个点确定一个圆；在同一直线上的 三个点不能作圆． 3．三角形的外接圆、圆的内接三角形．