- 2021-11-10 发布 |
- 37.5 KB |
- 23页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
第4章 第4节 透镜与透镜成像-2021年初中物理竞赛及自主招生大揭秘专题突破
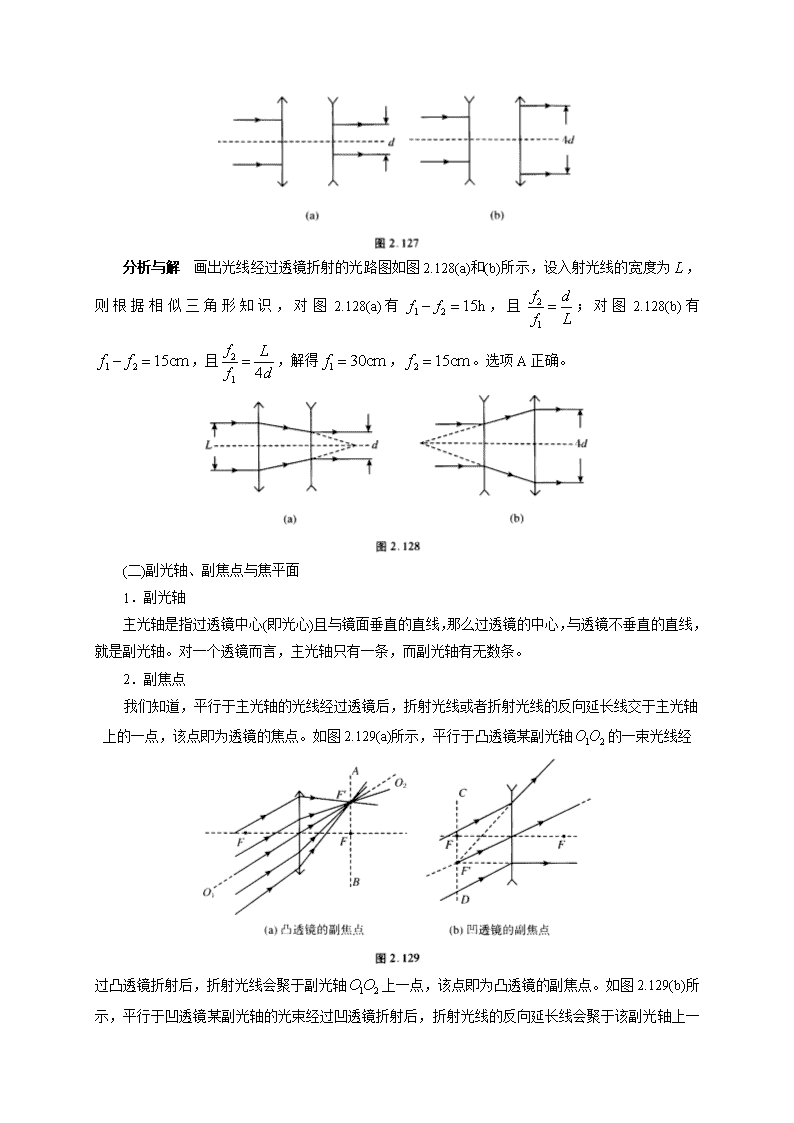
第四节 透镜与透镜成像 一、凸透镜与凹透镜 凸透镜是指中间厚、边缘薄的透镜,凹透镜是指中间薄、边缘厚的透 镜。因为其形状不同,对光线的作用、成像规律也不相同。理想情况下, 凸透镜和凹透镜的厚度认为足够小,通常可以画成如图2.124(a)和(b)的样子。 (一)凸透镜和凹透镜对特殊光线的作用 1.凸透镜的三条特殊光线 ①过凸透镜光心的光线,经过凸透镜折射后,传播方向不改变,如图 2.125 光线 a 所示; ②平行于主光轴的光线,经过凸透镜折射后,折射光线通过另一侧的焦点,如图2.125光线b 所 示; ③过凸透镜焦点的光线,经过凸透镜折射后,平行于主光轴射出,如图2.125光线 c 所示。 2.凹透镜的三条特殊光线 ①过凹透镜光心的光线,经过凹透镜折射后,传播方向不改变,如图2.126光线 a 所示; ②平行于主光轴的光线,经过凹透镜折射后,折射光线的反向延长线通过焦点,如图2.126光线 b 所示; ③正对着另一侧焦点入射的光线,经过凸透镜折射后,平行于主光轴射出,如图 2.126 光线c 所 示。 例 1 (上海第 28 届大同杯初赛)焦距为 1f 的凸透镜与焦距为 2f 的凹透镜的主光轴重合,光心间 距为15cm 。平行于主光轴的一束平行光通过两透镜后得到一束宽度为 d 的平行光束,如图 2.127(a) 所示,若将两透镜位置互换,将得到一束宽为 4d 的平行光束,如图 2.127(b)所示,则( )。 A. 1 30cmf , 2 15cmf B. 1 15cmf , 2 15cmf C. 1 30cmf , 2 20cmf D. 1 45cmf , 2 30cmf 分析与解 画出光线经过透镜折射的光路图如图 2.128(a)和(b)所示,设入射光线的宽度为 L , 则根据相似三角形知识,对图 2.128(a)有 1 2 15hf f ,且 2 1 f d f L ;对图 2.128(b)有 1 2 15cmf f , 且 2 1 4 f L f d ,解得 1 30cmf , 2 15cmf 。选项 A 正确。 (二)副光轴、副焦点与焦平面 1.副光轴 主光轴是指过透镜中心(即光心)且与镜面垂直的直线,那么过透镜的中心,与透镜不垂直的直线, 就是副光轴。对一个透镜而言,主光轴只有一条,而副光轴有无数条。 2.副焦点 我们知道,平行于主光轴的光线经过透镜后,折射光线或者折射光线的反向延长线交于主光轴 上的一点,该点即为透镜的焦点。如图 2.129(a)所示,平行于凸透镜某副光轴 1 2OO 的一束光线经 过凸透镜折射后,折射光线会聚于副光轴 1 2OO 上一点,该点即为凸透镜的副焦点。如图 2.129(b)所 示,平行于凹透镜某副光轴的光束经过凹透镜折射后,折射光线的反向延长线会聚于该副光轴上一 点,该点即为凹透镜的副焦点。一个透镜可以有无数个副焦点。透镜所有副焦点组成的面,叫做焦 平面,对于薄透镜,焦平面是过透镜的焦点 F 且与主光轴垂直的平面,图 2.129 中直线 AB ,CD 分 别是焦平面与纸面相交的直线,代表了焦平面的位置。一个凸透镜有两个焦平面,某条副光轴上的 副焦点实际上是该副光轴与焦平面的交点。 焦平面的概念在透镜作图中应用广泛,据此我们可以画出任意光线的折射光线。 例 2 图 2.130 所示为一个薄透镜,试着画出入射光线 AB 的折射光线,保留作图痕迹。 分析与解 由题可知光线 AB 不是透镜的三条特殊光线,因此考虑利用透镜的焦平面与副焦点 的概念,具体作图步骤如下: (1)过凸透镜右侧焦点 F 作主光轴的垂线 L ,则 L 为焦平面。 (2)过透镜光心作平行于光线 AB 的副光轴,该副光轴与焦平面的交点即为副焦点 F。 (3)入射光线 AB 的折射光线必经过副焦点 F,图2.131中的折射光线 BC 即为所求。 焦平面与副焦点的概念在求解一些组合透镜的焦距时十分有用,下面通过一道例题,讲解求解 组合透镜等效焦距的方法。 例 3 到如图 2.132 所示,两个薄凸透镜 1L , 2L 平行放置,且主光轴重合,彼此间距为 d ,组 成一个透镜组合。已知 1F , 2F 分别为凸透镜 1L , 2L 右侧的焦点,对应焦距分别为 1f , 2f ,试利用 你所掌握的光学知识求解该透镜组的等效焦距 f 。 分析与解 如图2.133所示,作平行于主光轴的入射光线,与凸透镜 1L 交于 A 点,该入射光线被 1L 折射后,折射光线交 2L 于 B 点,光线 AB 的延长线通过 1L 右侧的焦点 1F 。对于凸透镜 2L 来说, 光线 AB 是入射光线,我们通过下面的方法画出它经过 2L 后的折射光线:过 2L 的光心 2O 作平行于 光线 AB 的虚线,该虚线交 1L 于 C 点。过 2L 的焦点 2F 作垂直于主光轴的虚线,交 2CO 于 2F,则 2F 即为透镜 2L 的一个副焦点,连接 2BF ,则光线 2BF 即为光线 AB 经过 2L 后的折射光线。 2BF 与主 光轴交于 F 点,则 F 即为透镜组右侧的焦点,这里我们求出 F 到透镜 1L 的光心 1O 的距离作为透镜 组的焦距(此即“前焦距”, 2O F 称为透镜组的“后焦距”)。 由上述作图过程可知, 1 2 2 2 2 2 1COO F F O BO F△ △ △∽ ∽ ,则有 2 2 2 1 f F F d O C , 1 2 1 f d O B d O C 可得 2 2 2 2 1 F F f O B f d 又 2 2 2BO F F F F△ △∽ , 2 2 2 2 F F f f O B f d ,因此有 2 2 1 f f f f d f d ,解得 1 2 1 2 f ff f f d 或写成 1 2 1 2 1 1 1 d f f f f f 由等效焦距 f 的表达式,当两个透镜紧贴在一起,即 0d 时,上式简化为 1 2 1 2 f ff f f 或 1 2 1 1 1 f f f 。值得一提的是,通常我们把凸透镜的焦距取为正值,凹透镜的焦距取为负值,因此 上式对凸透镜与凹透镜组合、凹透镜与凹透镜组合,都是适用的。 二、透镜成像公式 凸透镜与凹透镜成像公式均为 1 1 1 u v f ,其中,物距 u 总是取正值,实像的像距取正值,虚 像的像距v 取负值,凸透镜的焦距 f 取正值,凹透镜的焦距 f 取负值。由透镜成像公式可得出像距 表达式 ufv u f 。 1.放大率 物体通过凸透镜既能成放大的像也能成缩小的像。我们用像的高度和物体的高度之比来表示透 镜的放大程度,叫做放大率,用 m 来表示。如图 2.134 所示,放大率的表达式为 m A B AB ,结合光 路 图 中 ABO A B O △ △∽ , 亦 可 得 vA Bm AB u f u f 。因此可知,无论物体通过透 镜成虚像还是实像,物体越靠近焦点位置, u f 越 小,所成像的放大率越大。表 2.2 给出了物距在不同范 围时凸透镜成像情况及像的放大率情况。 表 2.2 物距u 像距u 成像情况 放大率 m 2u f 2f v f 倒立缩小的实像 1m 2u f 2v f 倒立等大的实像 1m 2f u f 2v f 倒立放大的实像 1m u f v 不成像或像在无穷远 m u f v u 正立放大的虚像 1m 由表 2.2 可知,凸透镜在 2f u f 和u f 时,均存在放大率 1m 的情况。而对于凹透镜, 在透镜成像公式中,由于其焦点为虚焦点,焦距 f 代入公式时应取负号,凹透镜所成像总是虚像, 像距 v 代入公式时应取负号,因此有 1 1 1 u v f ,得 ufv u f ,其放大率 1v fm u u f , 这与凸透镜在 2u f 时一样,放大率 1m ,因此在一些问题中,应注意问题的多解性。 例 4 (上海第 30 届大同杯)物体通过凸透镜所成像的放大率为 6,若将物体靠近透镜 4cm ,则 所成像的放大率为 3,透镜的焦距可能为( )。 A.8cm B.12cm C. 20cm D. 24cm 分析与解 由题意,物体通过透镜成放大的像,则物体可能在距离透镜一倍焦距到两倍焦距之 间的位置,也可能在距离透镜一倍焦距以内的位置。而当物体靠近透镜时,放大率却减小了,说明 物体可能在距离透镜一倍焦距到两倍焦距之间的位置,移动后距离透镜不到一倍焦距的距离;或者 物体本身就一直在距离透镜一倍焦距之内。根据透镜成像公式 1 1 u v 1 f ,得 1 1 1 6u u f , 1 1 1 4 3 4u u f 解得 8cmf 或 1 1 1 6u u f , 1 1 1 4 3 4u u f 解得 24cmf 因此本题正确选项为 AD。 2.像与物的距离关系 在做凸透镜成实像的实验时,我们都有直接的经验:物体靠近凸透镜,像就远离凸透镜。亦即 “物远像近,物近像远”,下面我们推导凸透镜成实像时,像与物的距离变化关系。 设凸透镜焦距为 f ,成实像时物距为u ,像距为 v ,此时像与物的距离记为 L ,则 L u v 。 根据凸透镜成像公式得 1 1 1 u v f u v uv ,因为 2 2 u vuv ,可得 2 2 4 u v uv Lf u v u v 因此 4L f ,当且仅当 2u v f 时,像与物的距离取得最小值 4 f 。可见,当物体逐渐由很 远处(大于两倍焦距)靠近透镜一倍焦距处时,像逐渐远离凸透镜,但是像与物的距离却是先减小,再 增大。 例 5 (上海第 30 届大同杯)凸透镜的焦距大小为 20cm ,点光源位于透镜主光轴上距离光心 30cm ,现移动凸透镜,使点光源距离凸透镜100cm ,该过程中,点光源的像移动的路程为( )。 A. 25cm B.35cm C. 45cm D. 55cm 分 析 与 解 当 点 光 源 位 于 距 离 透 镜 1 30cmu 时 , 由 透 镜 成 像 公 式 , 得 此 时 的 像 距 1v 1 1 60cmu f u f ,即像距点光源的距离为 1 1 1 90cmL u v ;在透镜继续移动到距离点光源 100cm 的过程中,我们发现点光源与透镜之间的距离恰好等于 40cm ,即此时 2 2 40cmu f , 而这正是像离物体最近的距离,有 2 2 40cmv f ,像距点光源的距离变为 2 2 2 80cmL u v 。 可见,从 1L 到 2L 这个过程中,像实际上是向靠近点光源的方向移动了 1 1 2 10cms L L ;当透镜 距 离 点 光 源 3 100cmu 时 , 对 应 的 像 距 3 25cmv , 此 时 像 与 点 光 源 的 距 离 变 为 3 3 3 125cmL u v ,则从 2L 到 3L 这个过程中,像实际上是向远离点光源的方向移动了 2 3 2 45cms L L ,因此,整个过程中像移动的路程为 1 2 55cms s s 。正确选项为 D。本题 极易犯的错误就是只找到了像的初末位置,而误选 B 选项。 在凸透镜成像问题中,类似上述“极值”问题不在少数,读者朋友请看下例。 例 6 (上海第 30 届大同杯)凸透镜的焦距为 f ,点光源 S 和光屏 M 位于凸透镜的左右两侧,点 光源位于凸透镜的主光轴上,光屏与凸透镜的主光轴垂直并和点光源的距离保持 L 不变,且 4f L f 。左右移动凸透镜的位置,当光屏上的光斑最小时,凸透镜与点光源的距离为( )。 A. 2 L f B. 2 L f C. Lf D. L f L f 分析与解 如图 2.135 所示,设点光源与透镜的距离为u ,则光屏与透镜的距离为 L u ,设像 距为v ,由凸透镜成像公式 1 1 1 u v f ,可得 ufv u f 。当光屏上的光斑半径 r 最小时,光斑面积 最小。根据相似三角形的相关知识,可得光斑半径 r 与透镜半径 R 之比为 uf L uv L ur u f ufR v u f 化 简 可 得 r u L L R f u f , 结 合 基 本 不 等 式 u L f u 2 2u L L f u f ,当且仅当 u L f u 时,即u Lf 时, 不等式取等号,即 r 取得最小值。本题正确选项为 C。另外,当u f 时,v 值为负,按上述方式进 行讨论,C 选项同样成立。 3.像的移动速度问题 凸透镜成像时,当物体靠近凸透镜或者远离凸透镜时,像也会随之移动。但是像与物体移动的 距离并不相同,这也就说明像与物移动速度不同,我们以一个竞赛真题为例题,来说明这类问题的 解答方法。 例 7 (上海第 29 届大同杯复赛)在一个足够大的水平圆盘中心 O 点处固定放置一个焦距为 f 的 凸透镜,在透镜的主光轴上与透镜相距为 1 1r r f 处放一点光源 1S ,所成的像为 2S ,俯视图如图 2.136 所示。 背景知识: ①物体经过某位置时的速度可以用在很短的时间内移动的距离 s 与所用的时间 t 的比值来表示。 ②可以证明当 a b 时,近似有 2 2a a b a ab a 。 试结合以上背景知识求解下列问题: (1)若圆盘绕 O 点匀速转动时,如图 2.136 所示,光源 1S 与透镜 保持距离为 1r ,随透镜一起运动的速度为 1v ,则此时像 2S 的速度 2v 为多大? (2)若圆盘静止不动,光源 1S 沿透镜的主光轴以速度 1v 向透镜移动,则当 1S 与透镜的距离为u 时, 实像 2S 的移动速度 2v 为多大? 分析与解 (1)设像与透镜的距离为 2r ,则根据凸透镜成像公式,有 1 2 1 1 1 r r f ,可得 1 2 1 r fr r f 。 当圆盘匀速转动时,光源与像都做圆周运动,它们在相等时间内转过的弧长为 1l , 2l 与它们到透镜 的距离成正比,即 2 2 2 1 1 1 1 v l r f v l r r f ,因此得 1 2 1 v fv r f 。 (2)当光源距离透镜为 u 时,根据透镜成像公式,像距离透镜为 ufy u f ,设光源在极短的时 间 t 内,向透镜靠近了 u 的距离,则此时物距为 u u ,对应的像距为 y u u f u u f ,根 据速度公式,有 1 uv t , 2 yv t ,则 2 u u f uf u u f u fy y yv t t t 化简后有 2 2 2 2 2 u u f ufv u u u f u u f f t 结合u u 时, u u u , u f f 继续化简得 22 2 1 2 2 2 2 v fuf u fv tu f t u f u f 4.二次成像法(共扼法)测凸透镜焦距 当物体和屏的相对位置 L 不变,且间距 4L f 时,凸透镜置于物、屏之间,移动凸透镜能在屏 上得到两个清晰的实像,若凸透镜两次移动的距离为 d ,则可以证明透镜焦距为 2 2 4 L df L ,现 证明如下: 如图 2.137 所示,设第一次成像时的物距为u ,则第一次成像的像距为 v L u 。第二次成像 的物距为u d ,第二次成像的像距为u 。根据透镜成像的对称性,第一次成像时的像距应等于第二 次成像的物距,第一次成像时的物距也等于第二次成像的像距,两次成像的过程相当于物距、像距 对调。因此有 L u u d , 2 L du ,第一次成像时的像距 v L 2 L du ,结合透镜成像 公式 2 2 4 uv L df u v L ,得证。 值得一提的是,图 2.137 中第一次成像的放大率 1 vm u ,第二次成像的放大率 2 v um u v , 所以 1 2 1m m 。 例 8 如图 2.138 所示,两端开口的圆筒内嵌有一凸透镜,透镜主光轴恰好与圆筒中轴线重合。 为了测出该透镜的焦距以及透镜在圆筒内的位置,小李同学做如下实验:在圆筒左侧凸透镜的主光 轴上放置一点光源 S ,在圆筒右侧垂直凸透镜的主光轴方向固 定一光屏,点光源 S 与光屏的距离为 L 。左右移动圆筒,当圆 筒左端面距离点光源 S 为 a 时,恰好在光屏上成一个清晰的像; 将圆筒向右水平移动距离b ,光屏上又出现了一个清晰的像。 则凸透镜和圆筒左端面的距离 x 为________,该透镜的焦距 f 为________。 分析与解 第一次成像时,物距u a x ,透镜向右移动距离b 后是第二次成像,第二次成像 时的像距 v L a x b ,由于二次成像过程中第一次的物距等于第二次的像距,因此有 a x L a x b ,得 2 2 L a bx 。则第一次成像的物距 2 L bu a x ,第一次成像的 像距 2 L bv L a x ,由凸透镜成像公式可得 2 2 4 L bf L ,当然也可以由二次成像公式直接 得出焦距 2 2 4 L bf L 。本题正确答案为 2 2 L a b , 2 2 4 L b L 。 三、光具组成像问题 所谓光具组,是指两个或两个以上的光学元件组合在一起形成的一个成像系统,光具组中的各 个元件分别对光线进行反射、折射,并多次成像。解决这类问题的关键是要画出光线的传播路径, 并实际分析光线是否能通过某一光学元件成像。这里还应区分实像与虚像的形成原理:实像是光线 实际会聚形成的,虚像是光线的反向延长线会聚形成的。 例 9 (上海第 25 届大同杯初赛)如图 2.139 所示,平面镜水平放置 且镜面朝上,在镜面上方竖直放置一凸透镜,在凸透镜左侧主光轴上 两倍焦距处有一点光源 S ,关于点光源在该光具组中成像情况的判断, 正确的是( )。 A.两个实像,两个虚像 B.两个实像,一个虚像 C.一个实像,两个虚像 D.一个实像,三个虚像 分析与解 如图2.140(a)所示,点光源 S 可通过透镜在另一侧主光轴上的两倍焦距处成一个实像 1S ,该实像为折射光线的会聚点,而一些会聚光线经过 1S 后会入射到平面镜上,因此 1S 又会在平 面镜中成一个虚像 2S ,从 2S “发出”的光线不会再入射到凸透镜上,因此不会再继续成像;另如图 2.140(b)所示,点光源 S 亦可通过平面镜直接成一虚像 1S ,从 1S “发出”的光线有些会入射到透镜 中,又会在透镜另一侧主光轴上方的两倍焦距处成一实像 2S ,经过 2S 的光线不会入射到平面镜上, 因此不能再继续成像。综上所述,点光源 S 在该光具组中可以成两个实像,两个虚像,选项A正确。 例 10 如图 2.141 所示,在凸透镜的两个焦点处,垂直光 轴放置两个大小相同的平面镜,镜面相对。每个平面镜都关于 凸透镜的光轴上下对称。现在左侧平面镜的中心处挖出一个圆 孔,在凸透镜左侧两倍焦距处放一个点光源 S ,则点光源 S 在 该光具组中所成的虚像个数为( )。 A.一个 B.两个 C.无数个 D.一个也没有 分析与解 如图 2.142 所示,从点光源 S 发出的光线一 部分穿过左边平面镜中央的圆孔入射到凸透镜上,这些光线 的折射光线的延长线将经过点光源在另一侧 2F 处的像点 S ,折射光线经右侧的平面镜反射后,根据光的反射定律 及图中几何关系,这些反射光线恰通过凸透镜光心,在光心 处成一个实像。穿过光心的光线又恰从左边平面镜中央的圆 孔射出,并未入射到镜面上,因此整个过程中没有出现光线的反向延长线会聚于一点,故不会成虚 像,选项 D 正确。 练习题 1.如图 2.143 所示,光线 AB 经过某凸透镜的一个焦点,B 点在薄透镜上。已知 F 是该透镜的 另一个焦点。若使用圆规和刻度尺来确定透镜的位置,则还需知道的条件是( )。 A.光线 AB 经过的焦点位置 B.透镜光心的位置 C.光线 AB 经透镜后的折射光线 D.不需要任何条件 2.(上海第 29 届大同杯初赛)小明利用太阳光测量凸透镜的焦距,方法如图 2.144 所示。他注意 到让凸透镜正对阳光,但没有仔细调节纸片与透镜的距离。在纸片上的光斑并不是最小时,就测出 了光斑到凸透镜中心的距离 L ,则凸透镜的实际焦距( )。 A.一定小于 L B.一定大于 L C.可能等于 L D.可能小于 L ,也可能大于 L 3.如图 2.145 所示,在光具座上自左向右依次竖直放置一个凹透镜、凸透镜和平面镜,两个透 镜的主光轴重合,凸透镜的焦距为 f ,此时两个透镜之间的距离为 L 。在凹透镜的左侧有一水平平 行光束通过两个透镜后人射到平面镜上,经平面镜反射后,反射光恰能沿原来的光路返回,据此可 判断凹透镜的焦距为( )。 A. f B. L C. f L D. f L 4.如图 2.146 所示,当用眼睛去观察镜子时,光束似乎是从 M 处发散开来的,则透镜的焦距 是( )。 A. 0.5m B. 0.3m C. 0.2m D. 0.1m 5.(上海第 28 届大同杯初赛)如图 2.147 所示,遮光板 A 与光屏 B 平行且相距为 d ,在 A 的中 央挖一直径为 1d 的圆孔,并在孔内嵌入与孔等大的薄凸透镜 L 。现有一束平行光束垂直照射遮光板, 在光屏上形成了一个直径为 2d 的圆形光斑,则该凸透镜的焦距大小可能为( )。 A. 1 1 2 d d d d B. 2 1 2 d d d d C. 2 2 1 d d d d D. 1 1 2 d d d d 6.(上海第 31 届大同杯初赛)如图 2.148 所示,一束平行于凸透镜 1L 主光轴的平行光经透镜会聚 到焦点。现在 1L 的右侧一倍焦距内某位置处放置一障碍物 P ,且与 主光轴垂直,其中心有一个直径为 1d 的圆孔,圆心位于主光轴上, 在障碍物的右侧,距离障碍物 s 处垂直主光轴放置一个光屏(图中未 画出),屏上出现了一个直径为 2d 的圆形光斑。若在障碍物圆孔处 嵌入一块薄凹透镜 2L ,屏上恰好出现一个亮点,已知 10cms , 1 1cmd , 2d 0.5cm ,则凹透镜 2L 的焦距大小为( )。 A.30cm B. 25cm C. 20cm D.15cm 7.一束光线经过某光学元件后的出射光线如图 2.149 所示,则方框内放置的光学元件( )。 A.只能是平面镜或凸透镜 B.只能是凸透镜或凹透镜 C.只能是凹透镜或平面镜 D.平面镜、凸透镜和凹透镜均可 8.(上海第 28 届大同杯复赛)如果不慎在照相机镜头上粘上一个灰尘颗粒(如图 2.150),那么拍 摄的相片( )。 A.其上部将出现一个黑点 B.其下部将出现一个黑点 C.其上部和下部皆无黑点 D.其上部和下部各出现一个黑点 9.(上海第 28 届大同杯初赛)用普通照相机拍照时,要根据物距进行“调焦”,使用起来不太便 捷。有一种“傻瓜”照相机,只要将景物全部纳入取景区内,不论景物的远近,都能得到比较清晰 的像,从而使拍照的过程变得十分便捷。这种“傻瓜”相机不用调焦的奥秘是( )。 A.采用了长焦距的镜头,使远近不同的物体成像的位置相差不大 B.采用了短焦距的镜头,使远近不同的物体成像的位置相差不大 C.采用了长焦距的镜头,使远近不同的物体成像的位置相同 D.采用了短焦距的镜头,使远近不同的物体成像的位置相同 10.(上海第 24 届大同杯初赛)如图 2.151 所示, 1F , 2F 是凸透镜的焦点,S 是放在凸透镜前的 点光源 S 是 S 经凸透镜所成的像。当光源 S 沿平行主轴的方向向透镜移动时(始终保持 u f ),像 S 远离透镜移动的情况是( )。 A.沿平行主轴方向 B.沿 O 与 S 连线方向 C.沿 2F 与 S 连线方向 D.沿 1F 与 S 连线方向 11.如图 2.152 所示,凸透镜竖直放置,凸透镜焦距为 f , 现有一点光源 S 在凸透镜左侧以凸透镜两倍焦距处为圆心,在经 过主光轴的竖直平面内做顺时针圆周运动,直径为 D ,则 2f D f ,则在下列关于点光源所成像 S 运动轨迹的各图中, 正确的是( )。 A B C D 12.一块凸透镜被剖成对称的两半,并按图 2.153 所示对接。 一个物体 ab 置于凸透镜前两倍焦距处,则对凸透镜成像的描述 中,有可能正确的是( )。 A B C D 13.(上海第 31 届大同杯)如图 2.154 所示,点光源位于凸透镜的主光轴上(图中未画出凸透镜的 位置),当点光源位于 A 点处,像成于 B 点;当点光源位于 B 点处,像成于 C 点。已知 5cmAB , 10cmBC ,则凸透镜的焦距大小为( )。 A.1cm B.5cm C.30cm D. 60cm 14.一焦距为 f 的凸透镜,主轴和水平 x 轴重合,透镜左侧的 x 轴上有一点光源,点光源到透 镜的距离大于 f 而小于 2 f ,若将此透镜沿 x 轴向右平移 2 f 的距离,则在此过程中点光源经透镜所 成的像将( )。 A.一直向右移动 B.一直向左移动 C.先向右移动,接着向左移动 D.先向左移动,接着向右移动 15.(上海第 29 届大同杯)某人通过焦距为12cm 、直径为 4cm 的放大镜(薄凸透镜)看报纸,报 纸与放大镜之间的距离为3cm ,且与放大镜的主光轴垂直,保持放大镜的位置不变,眼睛始终位于 主轴上且在距离放大镜 24cm 位置处进行观测(不考虑眼睛的大小),报纸上有部分区域是“盲 区”(即眼睛观测不到),该区域的面积为( )。 A. 29 cm B. 25 cm C. 23 cm D. 22 cm 16.(上海第28届大同杯)用凸透镜成像时,定义像与物的大小之比为“放大率”,则在物体成像 的情况下( )。 A.物距一定时,焦距越小放大率越大 B.物距一定时,焦距越大放大率越大 C.焦距一定时,物体离同侧焦点越近放大率越大 D.焦距一定时,物体离凸透镜越近放大率越大 17.(上海第 29 届大同杯)将物距增大到原来的 3 倍时,通过凸透镜所成的像的大小是原来像的 1 6 , 则此时所成像的放大率可能为( )。 A. 1 4 B. 1 3 C. 1 2 D. 3 4 18.(上海第 31 届大同杯)物体的高度为12cm ,与凸透镜的主光轴垂直放置,经凸透镜成高度 为 6cm 的缩小的像。若将物体朝透镜方向靠近 24cm ,经凸透镜成高度为 30cm 的放大的像,则此 凸透镜的焦距大小可能为( )。 A.10cm B.15cm C. 20cm D. 25cm 19.(上海第 26 届大同杯初赛)如图 2.155 所示的两平面镜 AM 和 AN 成直角放置,凸透镜的主 光轴恰好是该直角的角平分线,凸透镜的光心为 O , A 点恰好是凸透镜的焦点,光源 S 位于主光轴 上,通过该系统,光源 S 所成的像为( )。 A.四个虚像,三个实像 B.四个虚像,一个实像 C.三个虚像,一个实像 D.三个虚像,两个实像 20.如图 2.156 所示,平面镜和凸透镜的主光轴垂直并处在凸透镜两倍焦距处,在凸透镜另一 侧两倍焦距处有一个点光源 S 。现将平面镜向凸透镜靠近,关于点光源所成的像,下述结论中错误 的是( )。 A.平面镜在移动过程中,最多只能成两个实像 B.平面镜移动到一定位置时,正好只成一个实像 C.平面镜移动到一定位置时,正好只成一个虚像 D.平面镜移动到一定位置时,正好既成一个实像,又成一个虚像 21.(上海第 23 届大同杯初赛)如图 2.157 所示,竖直放置的不透光物体(足够大)中紧密嵌有一凸 透镜,透镜左侧两倍焦距处,有一个与主光轴垂直的物体 AB ,在透镜右侧三倍焦距处竖直放置一 平面镜 MN ,镜面与凸透镜的主光轴垂直, B , N 两点都在主光轴上, AB 与 MN 高度相等且与 透镜上半部分等高。遮住透镜的下半部分,则在该光具组中,物体 AB 的成像情况是( )。 A.两个实像,一个虚像 B.一个实像,两个虚像 C.只有一个虚像 D.只有一个实像 22.(上海第12届大同杯复赛)如图2.158所示,在直角坐标系原点O 处放置平面镜 MN ,它与 x 轴成 45夹角。在 O 点正下方 15cms 处水平放置一焦距为10cm 的凸透镜。 A 为一点光源,则关 于凸透镜所成的像正确的是( )。 A.在凸透镜下方成一个实像,在凸透镜上方成一个虚像 B.只在凸透镜下方成一个实像 C.在凸透镜的下方、 y 轴的左右两侧各成一个实像,但左边的实像更靠近凸透镜 D.在凸透镜的下方、 y 轴的左右两侧各成一个实像,但右边的实像更靠近凸透镜 23.光源与光屏相距 0.9m 固定,将凸透镜放在它们之间的某一位置时,屏上成一放大的像;把 凸透镜移到另一位置时,屏上成一缩小的像。若第一次像的长度是第二次像的长度的 4 倍,则凸透 镜的焦距为________。 24.一物体经焦距为 24cm 的凸透镜成一个放大率为 1.5 的像,则物体到透镜的距离为________。 25.凸透镜的焦距为15cm ,一物体放在凸透镜前,要得到放大率为 3 的虚像,则物体离透镜 的距离为________。 26.(上海第 25 届大同杯初赛)如图 2.159 所示,不透光小圆盘 P 和小圆形发光面 S 的半径均为 R ,平行、竖直放置,两者相距 2d 。 在它们正中间放置一个焦距为 d 的凹透镜 L ,透镜的主光轴通过 P 和 S 的圆心。在 P 的右侧距 P 为 d 处,放置一平行于圆盘面的光屏 M (足够大),则不透光圆盘 P 在光屏 M 上形成的本影(发光面 S 发出的任何光线都不能进入该区域 内)面积为;不透光圆盘 P 在光屏 M 上形成的半影(发光面 S 发出的光线中只有部分能进人该区域内) 面积为________。不透光圆盘 P 在光屏 M 上形成的半影(发光面 S 发出的光线中只有部分能进人该 区域内)面积为________。 27.(上海第 20 届大同杯复赛)某人通过焦距为9cm 、直径为 6cm 的凸透镜看报纸。此时眼睛距离报纸15cm ,凸透镜距离报纸 6cm 。 设眼睛在透镜的主光轴上,报纸平面垂直于主光轴,如图 2.160 所示。 (1)此时报纸的像距眼睛有多远? (2)若报纸上密排着宽、高均为 0.3cm 的字,则他通过透镜至多能 看清同一行上几个完整的字(忽略眼睛瞳孔的大小)? 28.(上海第25届大同杯复赛)在做光学实验时,某同学需要将一束 平行光的宽度放大2倍,于是他在光束路径中放置了由两片透镜组成的透 镜组来达到此目的,如图2.161所示。若其中一片透镜是焦距为f的凸透 镜: (1)如果另一片透镜采用的是凸透镜,那么其焦距应为多少?应 置于何处? (2)如果另一片透镜采用的是凹透镜,那么其焦距应为多少?应 置于何处? 29.(上海第 26 届大同杯复赛)如图 2.162 所示,复印机的扫描 器由截面为正六边形、表面为镜面的柱体构成,正六边形的边长为 a 柱体可以绕转动轴 O 转动(如图所示)。在扫描器右侧并排竖直放置 一个薄透镜,透镜的焦距为 f,透镜的主光轴通过扫描器的转动轴 O 。在透镜右焦平面上放置一光 屏,光屏的中心位于主光轴上。现有一竖直光束,其延长线与转动轴的距离为 2 a ,从图示位置射向 扫描器。 (1)请用尺规作图,画出该光线通过系统后射到光屏上的位置。 (2)求射到主光轴上方光屏的光点到主光轴的最大距离 d 。 30.(上海第 28 届大同杯复赛)如图 2.163 所示,两个焦距分 别为 1f 和 2f 的薄透镜 1L 和 2L 平行放置,两透镜的光轴略微错开。 已知两透镜相距为 D , 1D f ,两光轴间的距离为 。以透镜 2L 的光心为原点,以其主光轴为 x 轴(向右为正方向),以向上方向为 y 轴正方向,在图示平面内建立直角坐标系。求此透镜组右侧的 焦点坐标。 31.(上海第 25 届大同杯复赛)薄膜干 涉是一种重要的光学现象,其装置如图 2.164 所示,将一块平板玻璃放置在 另一平板玻璃上,在一端夹入几张纸片,从而在两片玻璃表面之间形成一个 劈形空气薄膜,当某单色光垂直入射后,利用显微镜可观测到空气薄膜附近 明暗相间的条纹,当纸张数不同时,条纹数也不同。如图 2.164 所示,条纹 平行且等间距。某同学测量在相同范围内看到的亮条纹数,记录在表 2.3 中: 表 2.3 纸张数 2 6 10 12 14 条纹数 3 9 15 19 21 (1)请你分析上述数据,猜测单位长度内的条纹数与薄膜的顶角的关系。 (2)将一根金属丝替换纸片夹在两玻璃板之间,数出条纹数为 6 条,问:它的直径相当于几张纸 的厚度? (3)现在有两根粗细不相等(微有差别)的金属丝 A 和 B ,将 A 和 B 放在 钢质平台上,A 和 B 上面用一透明平板T 压住,如图 2.165 所示。则在T 和 钢质平台间形成了尖劈形空气薄层,在某单色光垂直照射下产生明暗相间的 条纹,试简述怎样判断 A 和 B 谁粗谁细。 参考答案 1.D。B 点是凸透镜上的点,则 B 点到凸透镜的两个焦点距离相等。以 B 点为圆心,BF 的长 度为半径画圆,交光线 AB 于 F,则 F为凸透镜的另一焦点,连接 FF ,并找到 FF 的中点O , 则O 点即为凸透镜的光心,至此透镜位置已确定。 2.D。纸片上的光斑不是最小,说明纸片放在了焦点之前,或者焦点之后。 3.D。要使光线经平面镜反射后能原路返回,需使光线垂直入射到 镜面上,光路图如图 2.166 所示, F 为凸透镜和凹透镜共同的焦点,则 凹透镜的焦距为 f L 。 4.D。如图 2.167 所示,找到 M 点关于平面镜的对称点 M ,当平 行光经凸透镜会聚于 M 点时,用眼睛观察平面镜,光线好像是从 M 点 发散开来的。显然, M 是凸透镜的焦点,则焦距为 0.3 0.2 0.1 m 。 5.AD。光屏的位置为图 2.168 所示的 1B , 2B 两个位置,当光屏在 1B 位置时,由相似三角形的 知识有 2 1 f d f d d ,解得 1 1 2 d df d d ;当光屏在 2B 位置时,由相似三角形知识有 2 1 d f f d d ,解 得 1 1 2 d df d d 。 6.C。如图 2.169 所示,障碍物 P 的圆孔内未加凹透镜时,光线会聚在 F 点,F 点为凸透镜的 焦点。当圆孔内加凹透镜后,凹透镜对光线有发散作用,最终光线会聚在光屏上的 E 点。根据光路 的可逆性,可将 E 点视为一个发光点,则 F 点为 E 通过凹透镜所成的虚像,由题给条件,可知物距 10cmu s ,又 1 1cmd , 2 0.5cmd ,可知像距大小 20 cm3v ,设凹透镜焦距大小为 f , 则由透镜成像公式,并考虑像距、焦距的正负,有 1 1 1 u v f ,代入数据有 1 1 1 2010 3 f , 解得 20cmf 。 7.D。满足题意的光学元件可以是平面镜、凸透镜和凹透镜,如图 2.170 所示。 8.C。照相机镜头是凸透镜,镜面上的灰尘颗粒不会成像在底片上,相片上也不会有黑点出现。 9.B。要得到清晰的像,就要使得像出现在底片上。用“傻瓜”照相机拍照时,无论景物远近, 都能得到清晰的像,说明物距的改变对像距大小的影响不大,就是说无论物距多大,像总是成在略 大于凸透镜一倍焦距的小范围内,因此,要求焦距非常小使物距总满足远大于2倍的焦距。 10.C。自光源 S 发出的平行于主光轴和过光心的两条入射光线,经透镜折射后的折射光线的 交点即为像 S 。由图 2.171 可知,当光源 S 沿平行于主光轴的方向向透镜移动时,像 S 沿着 2F 与 S 连线的方向远离透镜。 11.D。在点光源 S 运动的轨迹圆上找到位于圆心的上下左右方向的四个点,并逐一作出点光 源 S 经过这四个点时所成的像的位置,并根据凸透镜成实像时“物远像近,物近像远”的规律判断 出像的移动方向。 12.C。分别将两个透镜补完整,可知物体通过两个透镜所成的像均为等大、倒立的实像,且物 体通过两个透镜所成的像,分别位于补完整后上方透镜主光轴的上方和补完整后下方透镜主光轴的 下方,因此本题正确选项为C。 13.D。先确定凸透镜的大概位置。若点光源在 A 点时,在 B 点成的像是实像,则透镜一定在 A 和 B 之间,且 B 点在一倍焦距以外。这样再将物体放置在 B 点时,只会成像于 A 点,而不会成像于 C 点,因此透镜不在 A 和 B 之间。再假设透镜在C 点右侧,则两次成像过程均是像与物在透镜同侧, 而凸透镜所成虚像应该位于物体的外侧,因此透镜不在C 点右侧。可见,透镜只能位于 A 点左侧, 这正好符合凸透镜成虚像的情况。设点光源在 A 点时,物距为u ,则像距大小为 5cmu ,由凸透 镜成像公式得 1 1 1 5u u f ,当点光源在 B 点时,物距变为 5cmu ,像矩大小变为 15cmu , 由凸透镜成像公式得 1 1 5 15u u 1 f ,由以上两式解得 15cmu , 60cmf ,本题正确选 项为 D。 14.D。设透镜焦距为 f ,初始时点光源到透镜的距离为 0u 。透镜向右移动距离 2x x f , 物距变为 0u u x ,根据透镜成像公式,像距 v 满足 0 1 1 1 u x v f ,解得 v 0 0 f u x u x f ,则可 得点光源的像到点光源的距离 d 为 2 0 0 0 0 0 0 f u x f u x f fd u v u x u x f fu x f u x f 2 0 0 2fu x f fu x f 结合基本不等式 2 2 0 0 0 0 2 2f fu x f u x f fu x f u x f 当且仅当 2 0 0 fu x f u x f ,即 02x f u (即透镜左侧的 2 倍焦距点恰移动到点光源位置) 时,不等式取等号。可见 4d f 。当 02x f u 时,d 随 x 的增大而减小;当 02x f u 时,d 取 得最小值 4 f ;当 02 2f u x f 时,d 随 x 的增大而增大。由于点光源始终未移动,因此,点光 源的像先靠近,再远离点光源。 15.D。将眼睛视为一点光源,则从眼睛“发出”的光线,一部分沿直线传播直接照射到报纸 上,一部分被透镜折射后照射到报纸上,凡是报纸上有光 线照射的部分均为眼睛能看到的区域,光线照射不到的区 域为眼睛观测不到的“盲区”。根据凸透镜成像规律,可 知眼睛的像 S 位于透镜另一侧的两倍焦距处,画出如图 2.172所示的光路图,可知,图中以 OA 为半径的圆内均有 折射光线可以照射到,图中以OB 为半径的圆外均有从眼睛 直接发出的光线可以照射到,因此,照射不到的“盲区” 即为图中半径分别为OB ,OA 的两个圆之间的环形区域。结合三角形相似的知识,易得 9 cm4OB , 7 cm4OA ,因此可得自区的面积为 2 2 22 cms OB OA 。 16.D。由透镜成像规律 1 1 1 u v f ,解得 ufv u f ,所以放大率 v fm u u f 1 1u f 。 可见,u 和 f 越接近,放大率越大。 17.AD。设第一次成像时物距为 u ,像距为 v ,第二次成像时物距为3u ,像距为 v ,注意这 里假设的各量均取绝对值。则第一次成像的放大率为 vm u ,第二次成像的放大率为 3 vm u ,因 为第二次成像的大小是第一次成像大小的 1 6 ,即 1 6m m ,可得 1 2v v 。两次成像过程的可能情 况如下: (1)第一次成虚像,第二次成实像,则根据成像公式,分别有 1 1 1 u v f , 1 1 1 3u v f 结合 1 2v v ,则得 7 9 fu , 7 4 fv ,第二次成像的放大率为 3 3 4 vm u ,选项 D 正确。 (2)第一次成实像,第二次成实像,则根据成像公式,分别有 1 1 1 u v f , 1 1 1 3u v f 结合 1 2v v ,则得 5 3 fu , 5 4 fv ,第二次成像的放大率为 1 3 4 vm u ,选项 A 正确。 本题正确选项为 AD。 18.AB。设第一次成像时物距为u ,像距为 v ,则 6cm 1 12cm 2 v u ;由题知第二次成像时物距 为 24 cmu ,像距为 v 。则 30cm 5 24 cm 12cm 2 v u 下面分情况讨论成像情况: (1)若第一次、第二次均成实像,则根据成像公式,并将像距代入,有 1 1 1 1 2 u fu , 1 1 1 524 242 u fu 解得 45cmu , 15cmf 。 (2)若第一次成实像,第二次成虚像(像距取负值),则根据成像公式,并将像距代入,有 1 1 1 1 2 u fu , 1 1 1 524 242 u fu 解得 30cmu , 10cmf 。 综上所述,本题正确选项为 AB。 19.C。如图 2.173 所示,点光源 S 可通过平面镜成三个像 1S , 2S , 3S , 由题可知其中 1S , 3S 与透镜的距离恰为一倍焦距,因此 1S , 3S 不会再通 过透镜成像, 2S 位于透镜的两倍焦距处,因此可在透镜上方的两倍焦距处 成像 2S (图中未画出),但是可以看出经过透镜上方两倍焦距处的光线不会再 人入射到平面镜上,因此 2S 不会再继续成像。综上所述,该光具组共成三 个虚像,一个实像,选项 C 正确。 20.C。 S 本来是要在平面镜这一边的两倍焦距处成一个实像的,可是光线由于被平面镜挡住 而不能会聚于两倍焦距处,而是反射后向两倍焦距处关于平面镜的对称点会聚。当这个对称点仍在 透镜的平面镜这一侧(即平面镜在两倍焦距与一倍焦距之间)时,能够会聚成一个实像,这个实像在一 倍焦距以内,将再通过透镜成虚像,这是选项 A 和 D 的情况。而当平面镜在一倍焦距以内时,对称 点将在透镜的另一边,光线还没会聚又碰到透镜了,于是只能经透镜折射后成唯一的实像,跟 S 在 同一边,这是选项 B 的情况。只有选项 C 是不可能的,故选 C。 21.D。物体 AB 放在凸透镜的两倍焦距处,将在另一侧的 两倍焦距处成一个倒立、等大的实像 A B ,如图 2.174 所示。将透镜的下半部分遮住后,像的情况 并不改变。从 A , B 两点发出的光线经过透镜折射后,折射光线分别通过像点 A, B,由图可知, 折射光线并未入射到平面镜 MN 上,因此不会再成虚像。 22.D。 A 点到凸透镜的距离为 15cm 2cm 13cmu ,即 A 位于透镜一倍焦距和两倍焦距 之间,则 A 直接通过凸透镜成一个在透镜下方两倍焦距以外且在 y 轴左侧的实像 1A ,同时该像到 y 轴的距离大于10cm 。 A 通过平面镜成一个虚像 2A ,该虚像的坐标为 2, 10 ,由于自 A 出发、 经平面镜反射的光线可以入射到凸透镜上,因此 2A 可以通过凸透镜成像。 2A 到透镜的距离 15cm 10cm 25cmu , 2A 位于透镜两倍焦距以外,将成一个位于透镜一倍焦距与二倍焦距之 间,且位于 y 轴右侧的实像 3A ,同时 3A 到 y 轴的距离小于 2cm 。 23.0.2m 。这是凸透镜的共扼成像问题,第一次成放大的像,放大率应为 2,第二次成缩小的 像,放大率为 1 2 。因此第一次成像时物距与像距满足 1 2u v ,且 0.9mu v ,解得 0.3mu , 0.6mv 。再由透镜成像公式 1 1 1 u v f ,解得 0.2mf 。 24.40cm 或8cm 。设物距和像矩的大小分别为u 和 v ,则 1.5u v 。若像为实像,则根据透镜 成像规律 1 1 1 u v f ,解得 40cmu ;若像为虚像,则 1 1 1 u v f ,解得 8cmu 。 25.10cm 。略。 26. 216 9 R , 220 9 R 。首先确定发光面 S 的像 S 的位置,由 透镜成像公式 1 1 1 u v f ,注意凹透镜的焦距、像矩在公式中均应取 负值,则 1 1 1 d v d ,解得 2 dv ,则像的放大率为 1 2 va u , 所以发光面的像 S 在距离透镜 2 d 处,与发光面 S 位于透镜同一侧。由于自发光面 S 发出的任何一条 光线经过凹透镜折射后,折射光线的反向延长线必通过像 S ,因此,可以将 S 视为一个新的“光源”, 其发出的光(直线传播)在不透光圆盘 P 后留下影子,如图 2.175 所示。则以O 为圆心、CD 为直径的 圆即为本影区域,以 O 为圆心、CD 和 AB 为直径的两圆之间的环形部分即为半影区域,由几何知 识 可 得 4 3OC R , 2OA R , 因 此 本 影 面 积 为 2 24 16 3 9 RR , 半 影 面 积 为 2 2 2 4 202 3 9 RR R 。 27.(1) 27cm ;(2)20个。由题可知眼睛距离凸透镜 9cm ,恰位 于透镜的焦点上。设报纸的虚像像矩大小为 v ,则根据透镜成像公式, 有 1 1 1 u v f ,即 1 1 1 6 9v ,解得 18cmv ,因此报纸的像到眼 睛的距离为18cm 9cm=27cm 。将眼睛视为点光源,则眼睛“发出” 的光线经凸透镜折射后照射到报纸上的区域,即为眼睛能通过透镜看 到的范围。如图2.176所示,由于眼睛恰位于焦点,显然眼睛能看到的报纸上的区域为直径为 6cm 的 圆,因此位于该圆直径上的那一行字是能被看到的最多的一行字,即至多能看到 6cm 200.3cm 个字。 28.(1)有两解:放置一个焦距为 2 f 的凸透镜,放置在第一片透镜后3 f 处;放置一个焦距为 1 2 f 的凸透镜,放置在第一片透镜前 3 2 f 处。 (2)放置一个焦距为 2 f 的凹透镜,放置在第一片透镜前 1 2 f 处。 29.(1)如图2.177所示,先画出反射光线,该反射光线入射到凸透镜上,再画出该光线对应的副 光轴,找到副焦点,即可画出光线通过透镜后射到光屏上的位置。 (2)柱体从图示位置转过 60 ,入射点的法线与竖直方向的夹角从30 增加到 60 又减小到30 , 因此柱体在转动过程中,反射光线与入射光线的最大夹角为120 ,所以反射光线偏离主光轴(主光轴 上方)的最大夹角为30 ,作出与反射光线平行的副光轴交于焦平面,找到副焦点,并画出折射光线, 如图 2.178 所示,可见 3tan30 3d f f 。 30.如图2.179所示,沿 2L 主光轴入射的光线经 1L 折射后,折射光线交 2L 于 A 点,折射光线的 延长线过 1L 的焦点 1F ,根据虚焦点和焦平面的知识可画出光线经 2L 折射后的光线 2AF,其中 2F为 2L 的副焦点。由题给坐标系(未画出),结合数学知识,可知 A , 2F 。两点的坐标分别为 1 0, D f 和 2 2 1 , ff f ,直线 2AF叫的直线方程为 2 1 1 1 2 fD Dy f f f x f 。 如图 2.180 所示,沿着 1L 主光轴入射的光线经 1L 后传播 方向不变,交 2L 于C 点,经 2L 折射后,折射光线过 2L 右侧的焦点 2F ,由题给坐标系(未画出),结 合数学知识可知C , 2F 两点坐标分别为 0, 和 2 ,0f , 因此直线 2CF 的方程可表示为 2 2 y x f f 。光线 2AF , 2CF 的交点即为透镜组右侧的焦点 F ,焦点 F 的坐标即为 光线 2AF , 2CF 的方 程的 解,因 此可 得 F 的坐 标为 2 1 2 1 2 1 2 ,f f D f f f D f f D 。 31.(1)单位长度内条纹数与薄膜的顶角成正比关系。 (2)由内插法可知,直径相当于4张纸的厚度。 (3)可以在靠近 B 端施力向下压玻璃板,如果看到明暗相间的条纹变稀疏,则说明 B 比 A 的直径 要大。如果看到明暗相间的条纹变密集,则说明 B 比 A 的直径要小。查看更多