- 2021-11-10 发布 |
- 37.5 KB |
- 24页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
第2章 第3节 共点力的平衡-2021年初中物理竞赛及自主招生大揭秘专题突破
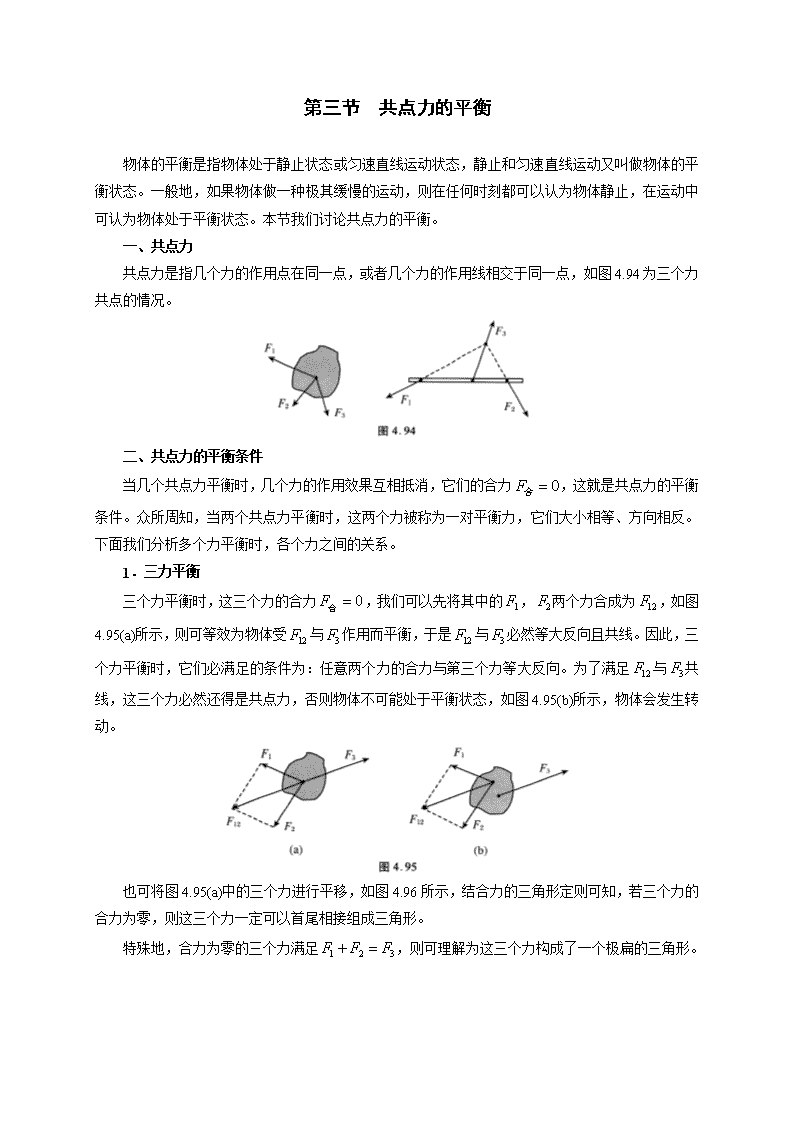
第三节 共点力的平衡 物体的平衡是指物体处于静止状态或匀速直线运动状态,静止和匀速直线运动又叫做物体的平 衡状态。一般地,如果物体做一种极其缓慢的运动,则在任何时刻都可以认为物体静止,在运动中 可认为物体处于平衡状态。本节我们讨论共点力的平衡。 一、共点力 共点力是指几个力的作用点在同一点,或者几个力的作用线相交于同一点,如图 4.94为三个力 共点的情况。 二、共点力的平衡条件 当几个共点力平衡时,几个力的作用效果互相抵消,它们的合力 0F 合 ,这就是共点力的平衡 条件。众所周知,当两个共点力平衡时,这两个力被称为一对平衡力,它们大小相等、方向相反。 下面我们分析多个力平衡时,各个力之间的关系。 1.三力平衡 三个力平衡时,这三个力的合力 0F 合 ,我们可以先将其中的 1F , 2F 两个力合成为 12F ,如图 4.95(a)所示,则可等效为物体受 12F 与 3F 作用而平衡,于是 12F 与 3F 必然等大反向且共线。因此,三 个力平衡时,它们必满足的条件为:任意两个力的合力与第三个力等大反向。为了满足 12F 与 3F 共 线,这三个力必然还得是共点力,否则物体不可能处于平衡状态,如图 4.95(b)所示,物体会发生转 动。 也可将图 4.95(a)中的三个力进行平移,如图 4.96所示,结合力的三角形定则可知,若三个力的 合力为零,则这三个力一定可以首尾相接组成三角形。 特殊地,合力为零的三个力满足 1 2 3F F F ,则可理解为这三个力构成了一个极扁的三角形。 例 1 (上海第 29届大同杯初赛)如图 4.97所示,长度为1m的均匀棒 AB通过细绳悬挂在光滑 的竖直墙面上的C点处。细绳与 AB棒连接于D点,BD的长度为 0.35m。不考虑棒的粗细,平衡 时 AB 棒与墙面之间的夹角 13 sin13 0.225,cos13 0.974 。则细绳 CD的长度约为 ( )。 A.1m B.0.8m C. 0.6m D. 0.4m 分析与解 棒静止,必处于平衡状态。对棒受力分析,其受竖直向下的重力G、垂直于墙壁的 弹力 N 、细线CD的拉力T ,这两三个力的合力为零,必是共点力。如图 4.98 所示, P为三个力 作用线的交点,O为棒的中点。则 0.5mOB , 0.5m 0.35m 0.15mOD , POD ,则 sin 0.1125mPB OB , cos 0.4870mOP OB ,由 DOP△ 与 DBC△ 相似,有 0.35 7 0.15 3 BC DB OP DO ,因此 7 1.1363m 3 BC OP ,在直角 PBC△ 中应用勾股定理,有 2 2 1.1419mPC BC PB , 由 7 3 DC PD , 且 1.1419mPD DC PC , 解 得 0.7993m 0.8mDC 。选项 B正确。 例 2 一个半径为 R、重为G的重球,用长度为 R的细绳悬挂在光滑的竖直墙壁上,悬线的延 长线恰好通过重球的球心,如图 4.99所示,用T 表示绳子对球的拉力,用 NF 表示墙对球的支持力, 下列结果中正确的是( )。 A. 3T G , 2NF G B. 2 3 3 T G , 3 3NF G C. 3 3 T G , 1 2NF G D. 3T G , 3 2NF G 分析与解 小球受细线拉力T 、墙壁支持力 NF 、重力G 三个共点力的作用,则其中任意两个 力的合力与第三个力等大反向,不妨把T 与 NF 合成为 F ,则 F 与G等 大反向,如图 4.100(a)所示。也可以将三个力平移,围成一个封闭三角 形,如图 4.100(b)所示,由题给条件,可知细线与墙壁夹角为30,则 在 力 的 三 角 形 中 , 利 用 三 角 比 可 得 cos30 F G T T , 解 得 2 3 cos30 3 GT G , tan 30 NF G , 3tan30 3NF G G ,选 项 B正确。 例 3 如图 4.101所示,两根长度相等的轻绳下端悬挂一个质量为m的物体,上端分别固定在 水平天花板上的M ,N 点,M ,N 间距为 s,已知两绳所能承受的最大拉力为T ,则每根绳的长 度不得短于________。 分析与解 当细线拉力为最大值T 时,物体受重力 mg 和两根细线的拉力T 的作用,设细线长 为 L,与竖直方向夹角为 ,则可画出细线拉力T 与重力围成的力的三角形如图 4.102所示,由几 何 关 系 有 2 cosT mg , cos 2 mg T 。 此 时 所 对 应 的 线 长 即 为 最 短 长 度 。 又 cos 2 mg T 2 2 2 sL L ,解得 224 TsL T mg 。 2.多个力平衡 (1)当物体受 N 个力作用而平衡时,其中任意一个力与其余的 1N 个力的贪力等六反向。且其 中m个力 m N 的合力与其余的 N m 个力的合力等大反向。 例 4 如图 4.103所示,处于水平面上的物体在斜向上的拉力 F 的作用下做匀 速直线运动。则物体所受拉力F 与地面摩擦力/的奋力的方向一定( )。 A.斜向右上方 B.竖直向上 C.斜向左上方 D.无法确定 分析与解 物体受四个力的作用:拉力 F 、重力G 、滑动摩擦力 f 和支持力 N ,由于不知道 拉力F 和滑动摩寧力的具体情况,因此直接求解它们的合力有困难。考虑到这 4个力的合力为零, F , f 的合力与G , N 的合力必等大反向,而G , N 的合力竖直向下,所以 F , f 的合力一定 竖直向上,本题正确答案为 B。 (2)物体受力平衡,则物体在任一方向上受力都是平衡的(正交分解法)。 当物体受到多个力作用时,以这些力的作用点为坐标原点,建立相互垂直的 x轴、 y 轴。将各 个力沿着 x轴、 y 轴的方向分解,则在 x轴、 y 轴轴方向上的所有分力的合力为零,即 0xF 合 , 0yF 合 这是处理多个力平衡时非常方便有效的方法。 例 5 如图 4.104所示,质量为 6kg的物体放在水平面上,在同一竖直平面 内,用大小为 20 2N 、方向与水平面成 45角的 1F 和大小为50N、方向与水平 面成 37角的 2F 两个力提它,物体仍静止不动。则物体受到的支持力大小为 ________,摩擦力大小为________,摩擦力方向是________。 分析与解 物体受到五个力的作用:拉力 1F 、拉力 2F 、重力G 、支持力N 以及静摩擦力 f 。 由于重力G和支持力在竖直方向,静摩擦力 f 沿水平方向,因此可选水平方向、竖直方向为坐标轴 将力分解,如图 4.105所示。由于物体静止,在坚宣和水平方向上,物体所受合力为零,则有: 水平方向: 1 2 2 4 2 5 F f F ,解得 2 1 4 2 40N 20N 20N 5 2 f F F 竖直方向: 1 2 2 3 2 5 F F N G ,解得 1 2 2 3 60N 20N 30N 10N 2 5 N G F F 例 6 如图 4.106所示,倾角为 的斜面上放置一重为G的木块,现将与斜面夹角为 斜向上 的拉力F 作用在木块上,木块仍静止。求: (1)斜面对木块的支持力 N ; (2)讨论木块所受的静摩擦力 f 。 分析与解 先对物体进行受力分析,物体一定受到的力是拉力 F 、重 力G 、支持力 N ,但是静摩擦力 f 的大小、方向均末知,因此不妨假设 静摩擦力 f 方向沿斜面向下,若求出的 f 为负值,则说明假设错误, f 方向沿斜面向上。画出各力 的示意图如图 4.107(a)所示,把各个力分解为平行于斜面方向和乗直于斜面方向的分力(即正交分解, 未画出坐标轴),各力的分力如图 4.107(b)所示。 (1)在垂直于斜面方向上,物体所受力的合力为零,则有 sin cosN F G ,解得 cos sinN G F (2)在平行于斜面方向上,物体所受力的合力为零,则有 sin cosf G F ,解得 cos sinf F G 现对上式讨论如下: ①若 cos sinF G ,则 0f ,静摩擦力 cos sinf F G ,方向沿斜面向下。 ②若 cos sinF G ,则 0f ,物体恰不受静摩擦力作用。 ③若 cos sinF G ,则 0f ,静摩擦力 sin cosf G F ,方向沿斜面向上。 三、共点力平衡的几种典型问题 (一)力的动态平衡问题 所谓动态平衡,是指物体在做某种极其缓慢的运动,整个过程中物体受到的力可能都在变化, 由于在运动过程中物体速度趋近于零,故在任一状态,均可认为物体静止,物体受力平衡。下面给 出解决这类问题的几种方法:, 1.公式法 公式法是求出未知力与角度、已知力(如重力)之间的关系,应用数学表达式求解力的变化过程的 方法。 例 7 如图 4.108所示,用细绳悬挂一个小球,小球在水平拉力 F 的作用下从平衡位置 P点缓 慢地沿圆弧移动到Q点,在这个过程中,绳子拉力T 和水平拉力 F 的大小 变化情况是( )。 A.T 不断增大, F 不断减小 B.T 不断减小,F 不断增大 C.T 与F 都不断增大 D.T 与 F 都不断减小 分析与解 小球受重力G 、拉力 F 、绳子的拉力T 的作用,我们可以试 着写出拉力F 与绳子拉力T 的表达式,由表达式判断它们的大小变化。不妨设 细线与竖直方向的夹角为 ,画出小球受到的力的示意图,因为小球缓慢移动, 因此三个力的合力为零,可以将拉力 F 与T 合成为 F ,则 GF ,如图 4.109 所示。在力的三角形中可得 cos GT , tanF G 。由于拉起小球的过程中 逐渐增大,可知T 与 F 都不断增大。本题正确选项为 C。 例 8 如图 4.110所示,人在岸边用跨过定滑轮的绳子拉 船,设水对船的阻力大小不变,在小船匀速靠岸的过程中,绳 的拉力F 和小船所受浮力F浮如何变化? 分析与解 船匀速前进的过程中受四个力的作用:重力 G 、拉力 F 、浮力 F浮和水的阻力 f 的作用。设绳子与水面 的夹角为 ,可以将拉力 F 沿着竖直和水平方向分解,如图 4.111所示。则 水平方向上有 cosF f ,由于 f 不变,拉船过程中 逐渐增加, cos 减小,因此拉力 F 遂渐蝤如。竖直方向上有 sinF F G 浮 ,由于 逐 渐增加,sin 逐渐增加,拉力F 也逐渐增加,而重力G 不变,因此F浮逐 渐变小。综上所述,拉船的过程中,拉力 F 逐渐增加,浮力 F浮逐渐减小。 2.图解法 我们知道,如果三个力平衡,则这三个力必组成首尾相接的封闭三角形。所谓图解法,即画出 由力组成的封闭三角形,根据三角形三个边边长的变化,来判断各个力的大小的变化情况。 例 9 如图 4.112所示,一小球放置在木板与竖直墙面之间。设墙面对球的弹力大小为 1N ,木 板对球的弹力大小为 2N 。以木板与墙连接点所形成的水平直线为轴,将木板从图示位置开始缓慢地 转到水平位置。不计摩擦,在此过程中( )。 A. 1N 始终减小, 2N 始终增大 B. 1N 始终减小, 2N 始终减小 C. 1N 增大后减小, 2N 始终减小 D. 1N 先增大后减小, 2N 先减小后增大 分析与解 如图 4.113(a)所示,小球受三个力作用,弹力 1N 与 2N 的合力与重力G等大反向,我们可以将 1N , 2N 和 重力G 平移,围成一个封闭三角形。如图 4.113(b)所示,在 挡板缓慢转到水平位置的过程中,重力的大小和方向均不变, 弹力的方向不变,而弹力 2N 将逆时针旋转且 2N 的末端始终 落在 1N 的作用线上。可见弹力 2N 逐渐变小,弹力 1N 逐渐减 小,本题正确选项为 B。 例 10 如图 4.114所示,重为G 的光滑小球静止在固定斜面和竖直挡板之间。若挡板绕底端逆 时针缓慢转到水平位置,在该过程中,斜面和挡板对小球的弹力的大小 1F , 2F 如何变化? 分析与解 如图 4.115(a)所示,小球受三个力作用,由于小球始终受力平衡,斜面对小球的弹力 1F 和挡板对小球的弹力 2F 的合力 F 与重力等大反向。将弹力 1F , 2F 以及重力G平移,围成封闭三 角形,其中力 1F 始终垂直于斜面,方向不变,力 2F 始终垂直于挡板,在挡板缓慢逆时针转动的过程 中,力 2F 将缓慢逆时针转动,但其末端始终落在 1F 的作用线上,如图 4.115(b)所示。当 2F 由初始位 置转向垂直于 1F 时, 2F 逐渐变小;当 2F 由垂直于 1F 的位置继续逆时针向上转动时, 2F 又逐渐变大。 可见, 2F 垂直于 1F 时, 2F 取得最小值。以上整个过程中, 1F 均为由 2F 的末端指向G起始端的有向 线段,因此 1F 始终减小。 例 11 用与竖直方向成 角(已知 45 )的倾斜轻绳 a和水平轻绳 b 共同固定一个重为G的小球。现保持小球在原位置不动,放长绳b并使其在 原竖直平面内逆时针缓慢转动,当绳b转过 角到 2的位置时,绳b上的拉 力为 2T ________;绳 b 再转过 角到 3 的位置时,绳 b 上的拉力为 3T ________。 分析与解 小球受重力G、轻绳a的拉力 aT 和轻绳b的拉力 bT 这三个力的作用, 将三个力平移并围成一个封闭三角形,如图 4.117所示,由于轻绳a与竖直方向夹角 不变,因此 aT 方向不变。当轻绳b由水平位置转过 角时,轻绳b的拉力 2T 恰与 aT 垂 直,因此 2 sinT G 。轻绳b继续转过 角时,绳b上的拉力 3T 与 1T 恰构成一个等 腰三角形的两个腰,即 3 1 tanT T G 。 由以上几个例子可知,在物体受三个力而平衡时,利用图解法可以很方便地判断力的变化情况, 尤其在三个力满足以下条件时,判断起来尤为方便:①一个力的大小和方向都不变(恒力);②一个力 只改变大小而不改变方向;③另一个力大小和方向都改变。 3.相似三角形法 相似三角形法是指利用力组成的三角形与几何线段组成的三角形相似,数据对应边成比例,判 断各力的变化情况。 例 12 如图 4.118所示, AC 是上端带定滑轮的固定竖直杆,质量不计的轻杆 BC一端通过铰 链固定在C点,另一端 B拴牢一根轻绳,轻绳下端悬挂一重为G 的物体。将另一根轻绳也拴在 B点, 上端绕过定滑轮 A,用水平拉力F 拉这根轻绳,开始时 160BCA ,现使 BCA 缓慢变小,直到杆 BC接近竖直杆 AC 。在此过程中(不计滑轮质量及 摩擦)( )。 A.拉力F 大小不变 B.轻杆的 B端所受轻杆的作用力大小不变 C.拉力 F 逐渐增大 D.轻杆的 B端所受轻绳的作用力先减小后增大 分析与解 分析杆上的 B点的受力情况, B点除了受两轻绳的拉 力外,还受到杆的弹力作用,由于杆为轻杆且可自由转动,因此杆受力 必沿着杆,否则杆不可能平衡。由此画出 B点的受力情况,并将轻绳 拉力 F 及杆 BC 对 B点的弹力 N 合成,则合力 F 与G 等大反向,如 图 4.119所示。观察可知由力组成的三角形与几何线段组成的三角形相 似,可得 G N F AC BC AB ,因为G ,AC ,BC大小均不变,则弹力 N 大小不变; AB变短时,力 F 变小。本题正确选项为 B。 例 13 如图 4.120所示,半径为 1.3mR 的半球置于水平地面上,在半球正上方天花板上悬挂 一根细线,细线末端拴一个重为 10NG 的小球,小球半径忽略不计。半径顶端距天花板为 0.7mH ,细线长度为 1mL 。求小球所受细线的拉力T 和大球对小球的弹力 NF 。 分析与解 画出小球的受力示意图,如图 4.121所示,设细线的拉力T与弹力 NF 的合力为F , 则 F 与重力 G 等大反向,由图中力组成的三角形与几何线揆组成的三用形相似,可得 NFG T H R R L ,可解得 6.5NN RF G H R , 5NLT G H R 。 4.其他动态变化问题 在有些力学平衡问题中,平衡状态不明显,需要我们根据力学规律和题给情景去判断物体在什 么条件下会处于平衡状态。下面举出几个例子。 例 14 如图 4.122 所示, A, B两物体的质量分别为 Am , Bm ,且 A Bm m ,整个系统处于 静止状态。滑轮的质量和一切摩擦均不计。如果绳一端由Q点缓慢地向左移到 P点,整个系统重新 平衡后,绳的拉力 F 和两滑轮间绳子与水平方向的夹角 的变化情况是( )。 A.F 变大, 变大 B. F 变小, 变小 C. F 不变, 变小 D.F 不变, 不变 分析与解 分析 A物体的受力情况,由于 A处于平衡状态,可知绳子拉力 AF m g , F 大小 恒定。分析悬挂 B物体的滑轮,滑轮受两侧绳子的拉力均为 F ,则两个拉力 F 的合力必竖直向上, 沿着绳子夹角的角平分线,因此易得两根绳子与水平方向的夹角均为 ,如图 4.123 所示,有 2 sin BF m g ,即 sin 2 2 B B A m g m F m ,所以在绳端由Q点缓慢地向左移到 P点的过程中,夹 角 保持不变,移动过程中绳子与滑轮的位置变化如图 4.123中的虚线所示。本题正确选项为 D。 例 15 如图 4.124所示,两根竖立的晾衣杆相距为 d ,将一长为 l l d 的细绳的两端 A,B分别固定在左、右两杆的某处。现通过轻质光滑动滑轮 将质量为m的物体挂在绳子上,静止后: (1)求绳子与竖直方向的夹角 的表达式(用三角比表示)以及绳子拉力 F 的大小。 (2)若保持绳子的 A端不动,将绳子的 B端在右杆上上下移动, 如何变 化?绳子拉力 F 的大小如何变化? (3)若保持绳子 A, B端在杆上的位置不动,使两杆靠近少许, 如何变化?绳子拉力 F 的大 小如何变化? 分析与解 由滑轮两侧绳子拉力相同,且拉力的合力竖直向上,得两侧 绳子与竖直方向的夹角相等,均为 。如图 4.125所示,设滑轮静止时所在 位置为O,延长 AO交右侧杆于C点,则由几何关系可知 COB△ 为等腰三 角形,因此绳长 l AC ,在直角 ADC△ 中,有 sin DC d AC l ,此即为 角度 的表达式。绳子拉力 F 满足 2 cosF mg ,即 2cos mgF ,结合 2 2 2cos 1 sin l d l ,得 2 22 mglF l d 。 (2)由 sin d l 可知,当绳子的 B端在右杆上上下移动时,并不会改变绳子两端点间的水平距 离(即两杆距离),得 不变。绳子拉力 2cos mgF 也不会改变。 (3)若绳子的 A, B端在杆上的位置不动,则两杆靠近时,绳子两端点的水平距离 d 变小,由 sin d l ,得 角将变小,而 cos 要变大,因此 2cos mgF 将变小。 本题的结论可以直接套用于类似题目。 (二)整体法与隔离法 在力学问题中,经常会出现两个或多个物体通过某种方式连接或联系在一起,比如,两物体通 过细线、轻杆、弹簧等相连,或者两个物体直接接触而组成一个系统,我们把这样的系统叫做连接 体。处理连接体问题最常用的方法就是整体法与隔离法。下面我们通过两道例题的讲解,帮助同学 们领会这种方法。 例 16 有一个直角支架 AOB, AO水平放置,表面粗糙;OB 竖直向下,表面光滑, AO上 套有小球 P,OB 上套有小球Q,两球质量分别为 1m 和 2m ,两球间由一根质量可忽略且不可伸长 的细绳相连,并在某一位置平衡,如图 4.126所示。现将 P球向左移一小段距离, 两球再次达到平衡。那么将移动后的平衡状态和原来的平衡状态比较,AO杆对 P 球的支持力 PN 和细绳上的拉力T的变化情况是( )。 A. PN 不变,T变大 B. PN 不变,T变小 C. PN 变大,T变大 D. PN 变大,T变小 分析与解 先对 P,Q两球进行受力分析,并设细线与竖直方向夹角为 , 如图 4.127所示。由于两球均平衡,则可分别对它们列出平衡方程。 对 P球: 1cosPN T m g (竖直方向) ① sinT f (水平方向) ② 对Q球: 2cosT m g (竖直方向) ③ sin QT N (水平方向) ④ 由以上四个式子,我们可以判断出 PN 和T 的大小变化情况:当 P球左移少许时, 角变小, sin 变小,cos 变大。由③式可得T变小,再将③式代入①式,可得; 2 1PN m g m g ,可见 PN 大小不变。像这样具体分析系统内某一个或某几个物体受力情况从而解决问题的方法,我们称之为 隔离法。 下面我们进行下列操作: 将③式代入①式,可得 2 1PN m g m g ⑤ 比较②和④两式可得 QN f ⑥ 可见,在⑤和⑥式中并没有出现绳子的拉力T。如果我们把两球及绳子视为一个整体, 绳子的拉力T 是整体内部的作用力,我们将其称为内力,而其他的力,比如,重力、 摩擦力、杆对球的弹力,是整体之外的物体对这个整体内某个成员施加的力,我们将 这样的力叫做整体受的外力。因为这种处理方法不需要考虑整体的内力,因此干脆用 一个点来表示这个整体,画出它所受外力的示意图如图 4.128所示。由此可直接得出 ⑤和⑥两式,从而直接判断出 PN 保持不变。但是由于⑤和⑥式中并没有出现绳子的 拉力T ,因此,还得继续分析整体内部某一个物体,即将这个物体与其他物体“隔离”出来,再用 一次隔离法,比如,分析小球Q (受力少,方便分析),得到③和④两式,即可顺利分析出绳子拉力 的变化情况。 在处理连接体问题时,若能熟练、灵活地利用整体法和隔离法,则往往能快速、有效地解决问 题。 例 17 一个挡板固定于光滑水平地面上,截面为 1 4 圆的柱状物体甲 放在水平面上,半径与甲相等的光滑圆球乙被夹在甲与挡板之间,没有 与地面接触而处于静止状态,如图 4.129所示。现在对甲施加一个水平 向左的力F ,使甲沿地面极其缓慢地移动,直至甲与挡板接触为止。设 乙对鑛板的压力为 1F ,甲对地面的压力为 2F ,在此过程中( )。 A. 1F 缓慢增大, 2F 缓慢增大 B. 1F 缓慢增大, 2F 不变 C. 1F 缓慢减小, 2F 不变 D. 1F 缓慢减小, 2F 缓慢增大 分析与解 将甲、乙视为一个整体,凡是其他物体作用在甲上或者乙上的力均为整体受到的力。 结合作用力和反作用的知识,甲对地面的压力和地面对甲的支持力大小均为 2F ,乙对挡板的压力和 挡板对乙的弹力大小均为 1F 。因此整体受到的四个力可以表述为推力F 、重力G总、地面对整体的 支持力 2F 和挡板对整体的弹力 1F 。以一个点表示甲、乙组成的整体,画出其受力示意图如图 4.130(a) 所示,则有 2F G 总, 1F F 。可见,甲对地面的压力 2F 不变。由于甲缓慢移动过程中推力 F 的 变化情况未知,因此仅由整体法无法判断出 1F 的变化情況,考虑隔离法。现对乙进行受力分析,乙 受到三个力的作用:重力G乙、挡板对乙的弹力 1F 和甲对乙的弹力 F甲乙,三个力组成的封闭三角形 如图 4.130(b)所示。当甲逐渐向左移动时, F甲乙的方向将逐渐顺时针转动,而 1F 方向不变,G乙的 大小和方向均不变,因此由三角形的动态变化可得 F甲乙逐渐变小, 1F 逐渐变小。本题正确答案为 C。 例 18 如图 4@131所示,质量均为m的Ⅰ,Ⅱ两木块叠放在水平面上,Ⅰ受到斜向上与水平 面成 角的力F 的作用,Ⅱ受到斜向下与水平面成 角的力 F 的作用,两力在同一竖直平面内,此 时两木块保持静止,则( )。 A.Ⅰ,Ⅱ之间一定存在静摩擦力 B.Ⅱ与水平面之间可能存在静摩擦力 C.Ⅱ对Ⅰ的支持力一定等于mg D.水平面对Ⅱ的支持力可能大于 2mg 分析与解 将两木块视为一个整体,则整体受重力 2mg、地面支持力 N 以及两个拉力 F 的作 用如图 4.132(a)所示。由于两个拉力 F 为平衡力,因此地面对木块Ⅱ的静摩擦力为零,整体竖直方 向上受力平衡,则可得 2N mg 。两木块之间的摩擦力是整体的内力,必须采用隔离法进行分析。 现隔离木块Ⅰ,如图 4.132(b)所示,木块Ⅰ受拉力 F 、重力mg和木坎Ⅱ对木块Ⅰ的支持力 1N 的作 用,可见,木块Ⅰ必受水平向左的摩擦力的作用,大小等于 cosF 。本题正确选项为 A。 (三)摩擦力参与下的物体平衡 1.静摩擦力的求解 静摩擦力作为一种“被动力”,其大小、方向完全由物体所受其他力的情况決定。在分析物体间 的静摩擦力的作用时,物体的平衡条件成为一把判定静摩擦力大小及方向的金钥匙。我们只需要先 分析出物体所受其他力的情况,再视情况结合假设法,往往可以使得问题迎刃而解。 例 19 如图 4.133所示,五本书相叠放在水平桌面上,用水平力 F 拉中间的书 c但未拉动,各 书仍静止。关于它们所受摩擦力的情况,以下判断中正确的是( )。 A.书 e受两个摩擦力作用 B.书b受到一个摩擦力作用 C.书 c受到两个摩擦力作用 D.书 a不受摩擦力作用 分析与解 将 a,b作为一个整体,如果 a,b整体在水平方向受到摩擦力,就不能处于平衡 状态,同理再单独分析 a,可知 a,b均不受摩擦力。分析书 e时,可以把 a,b , c, d 作为一 个整体,易知 d 与 e间存在摩擦力,把 a,b,c,d ,e作为一个整体,可知地面对 e必有摩擦力, 本题正确选项为 AD。 例 20 如图 4.134所示,在两块竖直的木板之间,有质量均为m的 4块相同的砖,用两个大小 均为F 的水平力压木板,使砖静止不动。则第 2块对第 3块砖的摩擦力的大小 为( )。 A.0 B.mg C. 2 mg D.2mg 分析与解 直接分析 2,3两块砖之间的静摩擦力有难度,因此可考虑采用整体法,由外向内逐 步分析。将 4块砖视为一个整体,则整体重力为4mg,由竖直方向上整体受力平衡和对称关系,可 得两木板对 1,4两块砖的静摩擦力为 2mg,方向竖直向上。再将 2,3两块砖作为整体,可得 2,3 两砖分别受到 1,4两砖施加的大小为mg、方向竖直向上的静摩擦力。至此,2,3两块砖均已受力 平衡,2,3两砖之间的静摩擦力为 0。本题正确答案为 A。值得注憙的是,本题切不可选 1,2为整 体,得出左边木板对 1以及 3对 2施加的静摩擦力均为mg的错误结论。这是因为 1,2整体左右两 边并不对称,因此它们所曼的静摩擦力的大小并不相等。 2.全反力问题初探 我们知道,滑动摩擦力与接触面间的弹力 NF 、接触面间的动摩擦因数 有 关,可用公式表示为 Nf F 。所谓全反力,就是物体所受滑动摩擦力与物体所 受支持力 NF 的合力,用 R表示。如图 4.135所示,设全反力 R与支持力 NF 的夹 角为,则 tan N f F ,可见,对子同一接触面,无论弹力和滑动摩擦力如何变化,虽然 R的 大小随之变化,但 R的方向恒定。这是一个很有用的结论。实际上,被称为摩擦角。值得注意的 是,一般认为最大静摩擦力等于滑动摩擦力,若是静摩擦力与弹力的合成,则 R与 NF 的夹角应介 于 0和之间,不可能大于。 例 21 如图 4.136所示,斜面静止在粗糙的水平地面上,一个小物体恰能沿斜面匀速下滑。若 以斜向下方向的力 F 向下推小物体,使小物体加速下滑,则( ) 。 A.斜面一定静止,且与地面之间没有摩擦力产生 B.斜面可能静止,且受到地面向右的静摩擦力 C.斜面一定运动,且受到地面向右的摩擦力 D.斜面一定静止,且受到地面向右的静摩擦力 分析与解 斜面体是否受地面的静摩擦力作用,取决于斜面体所受的 其他力的作用,易知斜面除了受竖直方向的重力和支持力外,还受到小物 体对其的作用力。现在从小物体入手来分析。小物体能沿着斜面匀速下滑,则其受力一定平衡。小 物体所受斜面的支持力 NF 和滑动摩擦力 f 的合力,即全反力 R一定与它的重力G等大反向。根据 作用力与反作用力的知识,小物体对斜面的压力 NF 和小物体对斜面体的滑动摩擦力 f 的合力 R (也是全反力)必竖直向下,如图 4.137所示。这样,斜面体受到的力都 在竖直方向上,水平方向的合力为零,因此斜面体没有水平方向的运动趋 势,不受地面的静摩擦力作用。当用一个斜向下的力 F 推小物体使得小 物体加速下滑时,小物体受力不再平衡,且小物体对斜面的压力 NF 要变 大,对应的小物体对斜面体的滑动摩擦力 f 也增加,但是注意到 Nf F , NF , f 是等比例增加的,其合力 R虽然也增加相同'的愤 数,但是R的方向仍竖直向下,因此,斜面体仍不受地面的静摩擦力作 用。本题正确选项为 A。 例 22 如图 4.138 所示,质量为m的物块与水平面间的动摩擦因数为 , 为使物块沿水平面做匀速直线运动,则所施加的拉力 F 至少应为多大?此时拉力 与水平方向的夹角应满足什么关系式? 分析与解 求解力的最小值问题,我们在前面讲过三个力平衡时,可以利用动态三角形来处理。 但是本题中物体受四个力:拉力F 、重力G以及支持力 NF 和滑动摩擦力 f 。不难想到可将 NF 和 f 合成为全反力 R,并设 R与弹力方向夹角为,则 tan N f F ,可得 R方向不变。至此,我 们就将四个力的平衡问题转化为三个力的问题。如園 4.139所示,画出全反力 R、拉力F 以及重力G 所围成的力的三角形,由于 R 方向不变,容易看出当 F 与 R 垂直时, F 取得最小值 minF , min sinF G , 结 合 tan , 由 数学 知 识 得 2 sin 1 , 因 此 min 21 GF 。结合图 4.139的几何关系可知,当拉力 F 取得最小值 minF 时, 拉力与水平方向的夹角满足 ,即 tan tan 。 练习题 1.(上海第 31届大同杯初赛)木块静止在水平桌面上,下列关于桌面对木块的弹力跟木块受到的 重力之间的关系的说法中,错误的是( )。 A.一对作用力和反作用力 B.—对平衡力 C.一对大小相等、方向相反的力 D.作用在同一物体上的力 2.在四个共点力 1F , 2F , 3F , 4F 的作用下,物体的平衡条件可表述为( )。 A. 1F , 2F , 3F , 4F 的合力为零 B. 1F , 2F , 3F 合力与 4F 大小相等,方向相反 C. 1F , 2F 的合力与 3F , 4F 的合力相同 D. 1F , 2F 的合力与 3F , 4F 的合力大小相等,方向相反 3.在同一平面内大小不同的三个共点力同时作用在一个物体上,以下各组力中,可能使物体平 衡的是( )。 A. 2N,3N ,6N B.1N , 4N,6N C.35N, 25N, 25N D.5N ,15N ,15N 4.一个物体在许多个共点力的作用下处于平衡状态,现使其中某个力 F 增大10N,为使物体 仍处于平衡状态,应该采取的措施是( )。 A.其他各个力都增大10N B.其他各个力的合力增大10N C.在力 F 的反方向加一个大小为10N的力 D.将与F 反方向的力减小10N 5.一个质点受到如图 4.140所示的五个共点力 1F , 2F , 3F , 4F , 5F 的作用,则物体所受合力 的大小为( )。 A. 42F B. 52F C. 4 5F F D. 4 5F F 6.图 4.141中重物的质量为m,轻细线 AO和 BO的 A,B端是固定的,平衡时 AO是水平的, BO与水平面的夹角为 , AO的拉力 1F 和 BO的拉力 2F 的大小是( )。 A. 1 cosF mg B. 1 cotF mg C. 2 sinF mg D. 2 sin mgF 7.(上海第 26届大同杯初赛)某人在车后用80N 的水平力推车使车在平直公路上匀速前近,突 然发现车辆前方出现情况,他马上改用120N的水平拉力使车减速,在减速的过程中,车受到的合 力大小为( )。 A. 40N B.80N C.120N D. 200N 8.(上海第 23届大同杯初赛)小明在广场上游玩时,将一充有氢气的气球系于一辆玩具小汽车上, 并将玩具小汽车放置在光滑的水平地面上,如图 4.142所示,无风时细绳处 于竖直方向,当一阵风沿水平方向吹向气球时,下列说法中正确的是( )。 A.小汽车可能被拉离地面 B.氢气球仍处于静止状态 C.小汽车一定沿地面滑动 D.小汽车仍处于静止状态 9.(上海第 22届大同杯初赛)如图 4.143所示,汽车在平直的公路上做匀速直线运动,则属于一 对平衡力的是( )。 A.汽车的牵引力和汽车所受的重力 B.汽车所受的重力和汽车对地面的压力 C.汽车所受的重力和地面对汽车的支持力 D.汽车对地面的压力和汽车所受的摩擦力 10.(上海第 22届大同杯复赛)如图 4.144所示,斜面上质量为m的物体 受到方向沿斜面向上、大小为7N的力 F 作用,物体静止在斜面上,则关于 斜面对物体的静摩擦力,以下说法中正确的是( )。 A.方向一定沿斜面向上 B.方向一定沿斜面向下 C.大小不可能大于 7N D.大小可能等于7N 11.(上海第 28届大同杯初赛)假设实心球体在空中下落时受到的空气阻力大小正比于球体半径 与球体速度的乘积。现有实心木球甲、乙和实心铁球丙从高空由静止下落,三球的半径关系为 R R R 甲 乙 丙,三球的质量关系为m m m 甲 乙 丙,若三球匀速到达地面的速度分别为 v甲,v乙, v丙,则三球落地时的速度大小关系是( )。 A.v v v 甲 乙 丙 B.v v v 甲 乙 丙 C. v v v 甲 乙 丙 D.无法确定 12.(上海第 31届大同杯初赛)如图 4.145所示,形状一样、质量相等 A,B的两个楔形物块放 置在水平桌面上,质量均为m的两个物块分别放在 A, B斜面上,其中, A斜面上的物体恰好匀 速下滑,而 B斜面上的物体静止在斜面上。 A, B斜面都始终保持静止, A, B对地面的正压力 分别为 AN , BN , A, B对地面的摩擦力分别为 Af , Bf 。则下列判断正确的是( )。 A. A BN N ; 0A Bf f B. A BN N ; 0B Af f C. B AN N ; 0B Af f D. B AN N ; 0A Bf f 13.拖把是由拖杆和拖把头构成的擦地工具(见图 4.146)。设拖把头的质量为m,拖杆质量可以 忽略;拖把头与地板之间的动摩擦因数为 ,重力加速度为 g,某同学用该拖 把在水平地板上拖地时,沿拖杆方向推拖把,拖杆与竖直方向的夹角为 。当 拖把头在地板上匀速移动时推拖把的力F 的大小为( )。 A. sin cos mg B. sin cos mg C. cos sin mg D. cos sin mg 14.在上海世博会最佳实践区,江苏城市案例馆中穹形门窗充满了浓郁的地域 风情和人文特色。如图 4.147所示,在竖直放置的穹形光滑支架上,一根不可伸长 的轻绳通过轻质滑轮悬挂一重物G ,现将轻绳的—端固定于支架上的 A点,另一 端从 B点沿支架缓慢地向C点靠近(C 点与 A点等高),则绳中拉力大小变化的情 况是( )。 A.先变小后变大 B.先变小后不变 C.先变大后不变 D.先变大后变小 15.(上海第 27届大同杯初赛)如图 4.148所示,两根细绳的一端与质量为 2kg的小球 A相连, 它们的另一端分别固定在竖直墙面上 B, B点两点,若对小球施加一个方向与水平面成 60 角 的拉力F ,使得细绳都能伸直,此时,AC 恰好水平,与 AB的夹角也为 60 。下列关于拉力 F 大小的说法正确的是( )。 A.最大值为 20 3N B.最大值为 40 3N 3 C.最小值为10 3N D.最小值为 20 3N 3 16.(上海第 27届大同杯初赛)如图 4.149所示,细绳一端固定在竖直墙面上,另一端与一个密 度分布均匀的球相连。现用手托住球,让球紧贴墙面,保持细绳上有一定的张力,让小球处于静止 状态,且细绳与小球的连接点恰好在球心的正上方。考虑在一般情况下,摩擦因数 均小于 1,则 在将手拿开的一瞬间( )。 A.小球可能会平衡 B.小球一定不会平衡 C.小球可能受到向下的摩擦力 D.小球一定受到向上的摩擦力 17.(上海第 26届大同杯初赛)如图 4.150所示,建筑工人施工时,需要将物体运送到高处。高 处的建筑工人通过定滑轮拉动绳子 ab,为防止物体与墙壁相碰,站定在地面上的另一个建筑工人还 需要用绳子bc拉住物体,使物体与墙壁的距离始终保持不变,则在物体缓慢上升的过程中( )。 A.绳 ab上的拉力增大,绳bc上的拉力减小 B.绳 ab上的拉力减小,绳bc上的拉力增大 C.两根绳上的拉力均增大 D.两根绳上的拉力均减小 18.如图 4.151所示,不可伸长的轻质柔软细绳 AO和 BO的节点为O,在O点悬吊重物G, 绳OA处于水平,重物G 处于平衡。如果保持O点位置不变,使 A点逐渐上移至C 点。随着 A点 逐渐上移,细绳 AO的拉力将( )。 A.逐渐增大 B.逐渐减小 C.先减小再增大 D.先增大再减小 19.(上海第 20届大同杯复赛)如图 4.152所示,晾晒衣服的绳子两端分别固定在两根等高的竖 直杆上,绳子的质量及绳子与衣架挂钩间的摩擦均忽略不计。原来衣服保持静止,一阵恒定的风吹 来,衣服受到水平向右的恒力而发生滑动,并在新的位置保持静止。则相比原来,在新的位置时( )。 A.挂钩左右两边绳的拉力不再相等 B.绳的拉力一定变大 C.绳对挂钩的作用力变大 D.绳对挂钩的作用力不变 20.(上海第 30届大同杯初赛)如图 4.153所示,在托乒乓球跑步比赛中,某同学将质畺为m的 球置于球拍光面中心,在运动过程中球受到的空气阻力与速度大小成正比,比例系数为 k ,运动中 球拍光面与水平方向夹角为 。不计球与球拍间的摩擦,若要球始终保持在位于球拍中心不动,则 做匀速直线运动时的速度为( )。 A. sinmg k B. cosmg k C. tanmg k D. cotmg k 21.(上海第 28届大同杯初赛)如图 4.154所示,轻杆CB能够以C为转轴在竖 直平面内自由转动,杆的 B端系一重为G 的物体,用一根细绳通过定滑轮 A系住 杆的 B端,另一端施加外力F ,使轻杆由图示位置( 按近30 )缓慢增大至150的 过程中,轻杆的 B端所受作用力的大小( )。 A.保掎不变 B.逐渐减小 C.遂渐增大 D.先增大后减小 22.(上海笫 28届大同杯初赛)如图 4.155所示,XOY 为直角支架,两根细绳的一端都拴在重物 P上,另一端分别固定于支架的 A,B两点。开始时,杆 XO、绳 BP水平,杆OY 垂直,绳 PA与 水平方向的夹角为60。现使支架绕过O点的水平轴在竖直平面内顺时针转动至杆OY 水平,在上 述过程中,绳 AP,BP的拉力 AT , BT 的变化情况是( )。 A. AT 减小, BT 先减小后增大 B. AT 减小, BT 先增大后减小 C AT 先减小后增大, BT 增大 D. AT 先增大后减小, BT 增大 23.(上海第 27届大同杯初赛)如图 4.156所示, A, B两小球的质量之比为3 :1,用轻质细杆 连接。同时用一根细绳将两个小球系住,绳子跨过光滑的定滑轮C,并设法让两球和轻杆组成的系 统保持平衡,则系统平衡时,绳与绳的长度之比为( )。 A.1:1 B.1: 2 C.1: 3 D.1: 4 24.(上海第 27届大同杯初赛)如图 4.157所示,竖直墙面OP和水平地面OQ均光滑,a,b两 小球所受的重力相等,相互之间还存在大小与距离的平方成反比的斥力作用,方向沿a,b连线。 现通过光滑竖直挡板挡住b球,使 a,b静止在如图 4.157所示的位置。若将挡板稍微向左水平移动 一小段距离,当a,b重新处于静止状态时( )。 A.a对b的作用力增大 B. a对b的作用力减小 C.水平地面OQ板对b的支持力不变 D.OQ板对b的支持力增大 25.(上海第 22届大同杯初赛)如图 4.158所示,物体 A靠在竖直墙面上,在竖直向上的力 F 的 作用下, A, B保持静止,物体 B的受力个数为( )。 A.2个 B.3个 C.4个 D.5个 26.(上海第 31届大同杯初赛)如图 4.159所示,半圆柱体 P放在粗糙的水平地面上,紧靠其右 侧有竖直挡板 S ,在 P和 S 之间放有一个质量均匀的光滑小圆柱体Q,整个装置处于静止状态。若 使 S 保持竖直且缓慢地向右移动一小段距离,在此过程中Q未落地且 P一直保持静止,则下列说法 中正确的是( )。 A. S 对Q的弹力逐渐减小 B.地面对 P的摩擦力遂渐增大 C. P,Q间的弹力先减小后增大 D. P对地面的压力不变 27.在粗糙水平地面上与墙平行放着一个截面为半圆的柱状物体 A,A与竖直墙之间放一光滑 圆球 B,整个装置处于静止状态。现对 B加一竖直向下的力 F ,F 的作用线通过球心,设墙对 B的 作用力为 1F ,B对 A的作用力为 2F ,地面对 A的作用力为 3F 。若 F 缓慢增大而整个装置仍保持静 止,截面如图 4.160所示,在此过程中( )。 A. 1F 保持不变, 3F 缓慢增大 B. 1F 缓慢增大, 3F 保持不变 C. 2F 缓慢增大, 3F 缓慢增大 D. 2F 缓慢增大, 3F 保持不变 28.两刚性球 a和b的质量分别为 am 和 bm 、直径分别为 ad 和 b a bd d d 将两球依次放入一 竖直放置、内径为 a a bd d d d d 的平底圆筒内,如图 4.161所示。设 a,b两球静止时对圆 筒侧面的压力大小分别为 1f 和 2f ,筒底所受的压力大小为 F ,已知重力加速度的大小为 g 。若所 有接触都是光滑的,则( )。 A. a bF m m g , 1 2f f B. a bF m m g , 1 2f f C. a a bm g F m m g , 1 2f f D. a a bm g F m m g , 1 2f f 29.如图 4.162所示,质量分别为 1m , 2m 的两个物体通过轻弹簧连接,在力 F 的作用下一起 沿水平方向做匀速直线运动( 1m 在地面, 2m 在空中),力F 与水平方向成 角,则关于 1m 所受支持 力N 和摩擦力 f 的表达式中正确的是( )。 A. 1 2 sinN m g m g F B. 1 2 cosN m g m g F C. cosf F D. sinf F 30.假设有 100个共点力作用在物体上,物体静止,其中一个力的大小为10N,方向向东,则 其余 99个力的合力大小为________,方向________;若其中的 30个力的合力大小为 20N,则其余 的 70 个力的合力大小为________;若将方向向东的大小为10N的力旋转90,则这 100 个力的合 力大小变为________。 31.如图 4.163所示,电线OA的 A端挂一重为 4N的电灯,细绳 AB拉住电线,拉力大小为3N , 且细线恰水平,则电线与竖直方向的夹角 等于________,电线对电灯的拉力大小等于________N。 32.如图 4.164所示,绳 AB水平,BC为轻杆,C处铰于墙上,BC与 AB的夹角为30,物 体所受重力为100N ,挂于 B 端,则绳 AB 的张力大小为________,杆 BC 所受的作用力大小为 ________。 33.同一平面上的三个共点力 1F , 2F 和 3F 作用于一物体上,物体处于平衡状态,已知 1F 和 2F 垂直, 2F 和 3F 的夹角为120,则这三个力的大小之比为 1 2 3: :F F F ________。 参考答案 1.A。水平桌面对木块的弹力作用在木块上,方向竖直向上;木块的重力作用在木块上,方向 竖直向下。它们是一对平衡力。 2.ABD。C项错在“合力相同”时,方向也是相同的。 3.CD。三个力能使物体平衡,即三个力的合力为零,这三个力必须能围成三角形。 4.BC。当各个力的方向不变时,这些力的合力与这些力的大小均成正比,力 F 增大10N,相 比初始值增大为原来的 10NF F 倍,则 F 以外的力应同时变为原来的 10NF F 倍,方能使得 F 以 外的力的合力增大10N,这样所有力的合力还是为零。或者在力 F 的反方向增加一个10N的力, 将力 F 增加的10N抵消。 5.B。根据多边形法则, 1F , 2F , 3F , 4F 首尾相接,它们的合力等于从 1F 的起始端指向 4F 末 端的有向线段,即 5F ,所以五个力的合力为 52F 。 6.BD。轻细线OA,OB的拉力 1F , 2F 的合力与重物所受重力等大反向。 7.D。车所受阻力为80N,当人用120N向后的拉力使车减速时,合力为 200N。 8.C。无风时,对气球和小车整体进行受力分析,气球受到的空气浮力小于整体的重力,小车 没有离开地面;有风时,细线将倾斜,整体受到水平方向的风力,由于地面光滑,小车将沿风的方 向运动,但竖直方向上气球受到的浮力不变,仍小于整体重力,因此小车不会被拉离地面。 9.C。略。 10.D。略,可参照例 21的解法和结论。 11.B。设空气阻力表达式为 f kRv ,则质量为m的球匀速下落时空气阻力与重力平衡,有 mg kRv ,解得 mgv kR ,结合题目条件可知 v v v 甲 乙 丙。本题正确选项为 B。 12.B。略,可参照例 21的解法和结论。. 13.B。将推拖把的力 F 分解为竖直向下的分力 cosF 和水平向右的分力 sinF 则拖把对地 面的压力 cosN mg F ,拖把所受滑动摩擦力 cosf N mg F ,水平方向上拖把 受力平衡,有 sinF f ,解得 sin cos mgF 。 14.C。略,可参照例 15的解法和结论。 15.BD。当绳 AB恰好伸直(无拉力)时,拉力 F 的竖直分力等于球的重力,有 sin 60F mg , 40 3 3 F N 。当绳 AC 恰好无拉力时,由角度关系可知此时绳 AB 的拉力大小也等于 F ,则 2 sin 60F mg , 20 3 3 F N 。因此 F 的取值范围为 20 3 40 3N N 3 3 F 。选项 BD正确。 16.BD。如图 4.165所示,将手拿开后,不妨取绳子与圆球的连接—点 A为转轴, 则圆球的重力G、绳子的拉力T 均没有转动效果。设圆球半径为 R,墙壁对球的支持 力N 的力矩为 NM NR ,对 A点的转动效果是顺时针方向,因此,墙壁对圆球的摩 擦力应沿墙壁向上,设为 f ,则 f 的力矩 fM fR 。考虑到 1 , f N N , 则 N fM M ,球要顺时针转动,不会平衡。本题正确选项为 BD。 17.C。本题若假设出角度,写出两绳子与角度的关系再判断绳子拉力的变化,将会非常烦琐, 因此考虑采用图解法。两绳的拉力 abF , bcF 的合力 F合与物体的重力等大反向,当物体逐渐上升时, 易得两绳与竖直方向的夹角均逐渐变大,则 abF , bcF 与 F合所构成的平行四边形也愈发扁长,如图 4.166所示,可知 abF , bcF 逐渐变大,本题正确选项为 C。 18.C。当绳OA与绳OB垂直时,绳OA的拉力最小。 19.C。同一根轻绳各处拉力相等,A项错误。衣服原来受重力和两 个绳的拉力而平衡,多了风力后是 4个力平衡,两个绳子的拉力的合力与 重力、风力的合力相平衡,故两个绳子的拉力的合力变大,即绳对挂钩作 用力变大,故 C项正确,D项错误。两个绳子的夹角变小,两个绳子的拉 力的合力变大,故两个绳子的拉力可能变大、变小或不变,故 B项错误。 20.C。设空气阻力为 f ,则 f kv 。乒乓球受力情况如图 4.167所示,将 f 与mg合成,由 几何关系可得 tan f mg ,因此可得 tanf mg , tanf mgv k k ,本题正确选项为 C。 21.A。提示:参照例 12的解法,利用相似三角形法。 22.B。小球受三个力的作用:绳子的拉力 AT , BT ,球的重力G,将 AT , BT 合成,设合力为F , 则 F G 。当直角支架顺时针缓慢转动过程中,可认为球所受重力G逆时针转动而直角支架不动, 则力F 亦保持大小不变逆时针转动。如图 4.168所示,力 F 逐渐转动的过程中,其分力 AT 逐渐减小, 而 BT 先逐渐增大,当 F 与 AT 垂直时, BT 取得最大值,此后,F 继续转动, BT 逐渐减小。因此本题 的正确选项为 B。 23.C。过C点作竖直线交 AB于O点,则O点即为两球组成的系统的重心位置,结合重心知 识易得 1 3 B A GAO OB G 。设杆对球的弹力大小为 F ,细线对球的拉力大 小为T ,画出两球所受各力围成的三角形如图 4.169所示,结合相似三 角形知识有 A AC CO T G , B BC CO T G ,因此 1 3 B A GAC BC G 。本题正确 选项为 C。 24.BC。可参照例 17的解法,采用整体与隔离法相结合分析。 25.C。本题若直接分析 B物体受力情况比较困难,不妨先将 A, B视为一个整体,则可判断 整体与墙壁之间并没有相互挤压,即 A不受墙壁对其的弹力。接下来单独对 A物体进行受力分析, 如图 4.170所示, A物体受 B对其施加的弹力 N 和静摩擦力 f 的作用, N 和 f 缺一,则 A物体不 能平衡。由此, A对 B同样有弹力 N 和静摩擦力 f 的作用,考虑到 B同时受到重力和推力 F 的 作用,因此 B物体共受四个力的作用。本题正确选项为 C。 26.BD。画出 P,Q的受力情况如图 4.171所示。当挡板 S 缓慢向右移动时,P对Q的弹力 F 将顺时针转动,而 F 的竖直分力应与Q球的重力 QG 等大反向,动态变化过程如图 4.172所示,可 见, F , QN 均逐渐增大。再对 P,Q用整体法,可知地面对 P的弹力 QP PN GG , PN 保持 不变,地面对 P的静摩擦力 Qf N , f 逐渐增大,综上所述,选项 BD正确。 27.C。作用在 B上的竖直向下的力 F 增大时,B仍保持平衡,则 A对 B的弹力 2F (该力沿 A, B圆心的连线)也增大,墙壁对 B的压力 1F 也将增大。B对 A的反作用力也增大,因此地面对 A的 支持力和静摩擦力都增大,即地面对 A的作用力 3F 增大。 28.A。提示:将 a,b两球视为一个整体,在水平、竖直方向对整体受力分析并列出平衡方程。 29.AC。提示:将 1m , 2m 视为一个整体,则竖直方向有 1 2sinF N m g m g ,解得 1 2 sinN m g m g F ,水平方向有 cosf F 。 30.10N,西向; 20N;10 2N。提示:100个力平衡,则10N的力与其余 99个力的合力 等大反向;其中 30个力的合力与其余 70个力的合力也等大反向;当方向向东的力旋转90后,这 100个力的合力相当于两个互相垂直的10N的力的合力。 31.37,5。略。 32.100 3N, 200N。提示:CB为轻杆,则两绳拉力的合力方向必沿着轻杆。 33. 3 :1: 2。提示:三个力所围成的封闭三角形为直角三角形,三边之比即为力的大小之比。查看更多