人教版 九年级 数学 总复习 第二讲 解直角三角形（教师版）

人教版 九年级 数学 总复习 第二讲 解直角三角形（教师版）

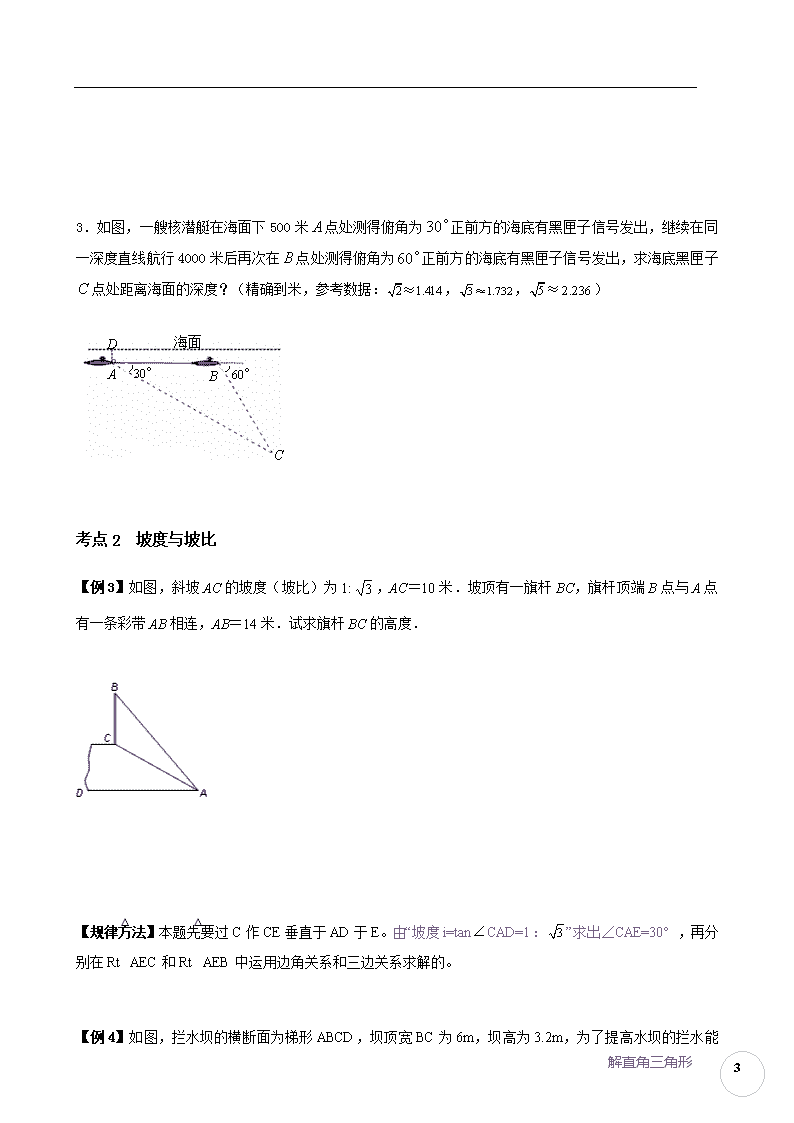
解直角三角形 1 第二讲 解直角三角形 明确目标﹒定位考点 锐角三角函数是沟通代数与几何知识的桥梁，它剥去代数知识的外表转化为解直角三角形的问题， 或以锐角三角函数知识为工具将几何知识转化为解代数问题，从而将平面几何中对直角三角形的研究转化 为定量研究，达到化难为易的目的，在中考中的考察较为频繁，在综合性的大题中通常与其他知识点相结 合考查，所占的分值在 10-12 分左右。 热点聚焦﹒考点突破 考点 1 仰角与俯角 【例 1】 为了测量停留在空中的气球的高度，小明先站在地面上某点观测气球，测得仰角为 30°，然后 他向气球方向前进了 50m，此时观测气球，测得仰角为 45°．若小明的眼睛离地面 1.6m ，小明如何计算 气球的高度呢（精确到 0.01m） 【规律方法】此题是在两个直角三角形中，运用三角函数列出边角关系，设两个未知数列两个方程求解的。 但是它也可以设一个未知数，在两个直角三角形中，运用边角关系（三角函数）分别把 AD、BD 用含 h 的 代数式表示出来，代入等量关系：AD—BD=AB，得到一个方程，进行求解。 【例 2】在学习实践科学发展观的活动中，某单位在如图所示的办公楼迎街的墙面上垂挂一长为 30 米的宣 传条幅 AE，张明同学站在离办公楼的地面 C 处测得条幅顶端 A 的仰角为 50°，测得条幅底端 E 的仰角 为 30°. 问张明同学是在离该单位办公楼水平距离多远的地方进行测量？ （精确到整数米）（参考数据：sin50°≈0.77，cos50°≈0.64，tan50°≈1.20， sin30°=0.50，cos30°≈0.87，tan30°≈0.58） 【规律方法】（1）根据题意构造直角三角形，利用其公共边构造方程求解． （2）根据题目中的情景，结合解三角形的知识设计测量方法． 解直角三角形 2 【变式训练 1】 1．如图，热气球的探测器显示，从热气球看一栋高楼顶部的仰角为 60 ，看这栋高楼底部的俯角为 30 ， 热气球与高楼的水平距离为 60 m，这栋高楼有多高？（结果精确到 0.1 m，参考数据： 73.13  ） 2．如图所示，小华同学在距离某建筑物 6 米的点 A 处测得广告牌 B 点、C 点的仰角分别为 52°和 35°， 则广告牌的高度 BC 为__________米(精确到 0.1 米)．(sin35°≈0.57，cos35°≈0.82，tan35°≈0.70； sin52°≈0.79，cos52°≈0.62，tan52°≈1.28) 3．如图，一艘核潜艇在海面下 500 米 A 点处测得俯角为 30°正前方的海底有黑匣子信号发出，继续在同 一深度直线航行 4000 米后再次在 B 点处测得俯角为 60°正前方的海底有黑匣子信号发出，求海底黑匣子 C 点处距离海面的深度？（精确到米，参考数据： 2 1.414≈ ， 3 1.732≈ ， 5 2.236≈ ） 考点 2 坡度与坡比 【例 3】如图，斜坡 AC 的坡度（坡比）为 1: 3 ，AC＝10 米．坡顶有一旗杆 BC，旗杆顶端 B 点与 A 点 有一条彩带 AB 相连，AB＝14 米．试求旗杆 BC 的高度． A B C D6 米 52° 35° 30° 60°BA D C 海面 C A B 解直角三角形 3 【规律方法】本题先要过 C 作 CE 垂直于 AD 于 E。由“坡度 i=tan  CAD=1： 3 ”求出∠CAE=30° ，再分 别在 Rt △ AEC 和 Rt △ AEB 中运用边角关系和三边关系求解的。 【例 4】如图，拦水坝的横断面为梯形 ABCD，坝顶宽 BC 为 6m，坝高为 3.2m，为了提高水坝的拦水能 力，需要将水坝加高 2m，并且保持坝顶宽度不变，迎水坡 CD的坡度不变，但是背水坡的坡度由原来 的 i=1：2 变成 i′=1：2.5，（有关数据在图上已注明）．求加高后的坝底 HD 的长为多少？ 【规律方法】此题严格按照“坡度 i= 对边 邻边 ”，在两个直角三角形中列式计算的，它把梯形分割成了两个直角 三角形和一个矩形。 【变式训练 2】 1．如图，小阳发现电线杆 AB 的影子落在土坡的坡面 CD 和地面 BC 上，量得 CD=8 米，BC=20 米，CD 与地 面成 30º角，且此时测得 1 米杆的影长为 2 米，求电线杆的高度 解直角三角形 4 2．同学们对公园的滑梯很熟悉吧？如图，是某公园新增设的一台滑梯，该滑梯高度 AC＝2 米，滑梯着地 点 B 与梯架之间的距离 BC＝4 米． （1）求滑梯 AB 的长（精确到 0.1 米）； （2）若规定滑梯的倾斜角（∠ABC）不超过 45°，属于安全．通过计算说明这架滑梯的倾斜角是否符合要 求？ 3．我市某区为提高某段海堤的防海潮能力，计划将长 96m 的一堤段（原海堤的横断面如图中的梯形 ABCD） 的堤面加宽 1.6m，背水坡度由原来的 1:1 改成 1:2，已知原背水坡长 AD=8.0m，求完成这一工程所需的 土方。（精确到百位） （注:坡度=坡面与水平面夹角的正切值；提供数据: 2 1.41, 3 1.73, 5 2.24   ） 考点 3 方向角 【例 5】海船以 5 海里/小时的速度向正东方向行驶，在 A 处看见灯塔 B 在海船的北偏东 60°方向，2 小时 后船行驶到 C 处，发现此时灯塔 B 在海船的北偏西 45°方向，求此时灯塔 B 到 C 处的距离． 解直角三角形 5 【规律方法】解一般三角形的问题一般可以转化为解直角三角形的问题，解决的方法就是作高线，构造直 角三角形． 【变式训练 3】 1．如图，在航线l 的两侧分别有观测点 A 和 B，点 A 到航线l 的距离为 2km，点 B 位于点 A 北偏东 60°方 向且与 A 相距 10km 处．现有一轮船从位于点 B 南偏西 76°方向的 C 处，正沿该航线自西向东航行，5min 后该轮船行至点 A 的正北方向的 D 处． （1）求观测点 B 到航线l 的距离； （2）求该轮船航行的速度（结果精确到 0.1km/h）．（参考数据： 3 1.73≈ ，sin76 0.97°≈ ，cos76 0.24°≈ ， tan76 4.01°≈ ） 2．如图，MN 表示某引水工程的一段设计路线，从 M 到 N 的走向为南偏东 30°，在 M 的南偏东 60°方向上 有一点 A，以 A 为圆心、500m 为半径的圆形区域为居民区．取 MN 上的另一点 B，测得 BA 的方向为南偏东 75°．已知 MB＝400m，通过计算回答，如果不改变方向，输水管道是否会穿过居民区． 北 东 C D B E A l 60° 76° 解直角三角形 6 3．台风是一种自然灾害，它以台风中心为圆心在周围数十千米范围内形成气旋风暴，有极强的破坏力， 如图 11，据气象观测，距沿海某城市 A 的正南方向 220 千米 B 处有一台风中心，其中心最大风力为 12 级， 每远离台风中心 20 千米，风力就会减弱一级，该台风中心现在以 15 千米／时的速度沿北偏东 30°方向往 C 移动，且台风中心风力不变，若城市所受风力达到或超过四级，则称为受台风影响． （1）该城市是否会受到这次台风的影响？请说明理由． （2）若会受到台风影响，那么台风影响该城市的持续时间有多长？ （3）该城市受到台风影响的最大风力为几级？ 归纳总结﹒思维升华 1．仰角、俯角的定义 如右图，从下往上看，视线与水平线的夹角叫仰角，从上往下看，视线与水平 线的夹角叫做俯角．右图中的∠2 就是仰角，∠1 就是俯角． 2．坡角、坡度的定义 解直角三角形 7 坡面的铅垂高度与水平宽度的比叫做坡度 (或坡比)，读作 i，即 i＝AC BC ，坡 度通常用 1:m 的形式，例如上图的 1:2 的形式。坡面与水平面的夹角叫做 坡角。 从三角函数的概念可以知道，坡度与坡角的关系是 i＝tanB。显然，坡度越大，坡角越大，坡面就越 陡。 3.在解答三角函数应用题时，通常都能把它们化归到以下几个几何模型： 通过作高，把一般三角形或梯形构造出两个直角三角形，在两个三角形中分别运用三角函数的知识进行解 答。 专题训练﹒对接中考 解答题。 1．如图，小山岗的斜坡 AC 的坡度是 3tan 4   ， 在与山脚C 距离 200 米的 D 处，测得山顶 A 的仰角为 26.6 ，求小山岗的高 AB ． 2．为测山高，在点 A 处测得山顶 D 的仰角为 31°，从点 A 向山方向前进 140 米到达点 B，在 B 处测得山 顶 D 的仰角为 62°（如图）． （1）在所给的图②中尺规作图：过点 D 作 DC⊥AB，交 AB 的延长线于点 C； （2）山高 DC 是多少（结果取整数）？ 第 20 题 图① 图② 31 A D 62 B 笫 22 题 解直角三角形 8 3．如图，AB是高为60米的铁塔，分别在河边D处测得塔顶A的仰角为60°，在与B.D同一直线上的河对岸C 处测得塔顶A的仰角为40°. （1）求D点到铁塔距离DB的长；（结果保留根号） （2）求河岸间CD的宽度.（结果取整数） 4.如图8 ，某无人机于空中 A 处探测到目标 B、D 的俯角分别是30 、60  ,此时无人机的飞行高度 AC 为60m ， 随后无人机从 A 处继续水平飞行30 3 m 到达 A 处. (1)求 A、B 之间的距离. (2)求从无人机 A 上看目标 D 的俯角的正切值. 解直角三角形 9 5.如图 10， 在东西方向的海岸线 MN 上有 A、B 两艘船，均收到已触礁搁浅的船 P 的求救信号，已知船 P 在船 A 的北偏东 58°方向，船 P 在船 B 的北偏西 35°方向，AP 的距离为 30 海里. （1） 求船 P 到海岸线 MN 的距离（精确到 0.1 海里）； （2） 若船 A、船 B 分别以 20 海里/小时、15 海里/小时的速度同时出发，匀速直线前往救援，试通过计 算判断哪艘船先到达船 P 处. 作业： 一、 选择题。 1．如图，从热气球 C 处测得地面 A、B 两点的俯角分别为 30°、45°，如果此时热气球 C 处的高度 CD 为 100 米，点 A、D、B 在同一直线上，则 AB 两点间距离是（ ） A．200 米 B．200 3米 C．220 3米 D．100( 3＋1)米 第 1 题图 A B C D 30° 45° 解直角三角形 10 第 1 题图 二、填空题。 1．如图，两建筑物 AB 和 CD 的水平距离为 24 米，从 A 点测得 D 点的俯角为 30°，测得 C 点的俯角为 60°，则建筑物 CD 的高为______米．（结果保留根号） 2.（2015 年番禺区一模.16,3 分）如图，从一运输船的点 A 处 观测海岸 上高为 41m 的灯塔 BC（观测点 A 与灯塔底部 C 在一个水平面上）， 测得灯塔顶部 B 的仰角为 35°，则点 A 到灯塔 BC 的距离约为 （精确到 1 cm ）． 3．如图，有A 、B 两艘船在大海中航行， B 船在A 船的正东方向，且两船保持20 海里的距离，某一时 刻这两艘船同时测得在A 的东北方向，B的北偏东150方向有另一艘船C ，那么此时船C 与船B的距离是 ________海里．（结果保留根号) 三．解答题： 1.如图，两座建筑物 AB 及 CD，其中 A，C 距离为 50 米，在 AB 的顶点 B 处测得 CD 的顶部 D 的仰角β＝30°， 测得其底部 C 的俯角α＝60°，求两座建筑物 AB 及 CD 的高度(精确到 0.1 米)． 第 2 题 解直角三角形 11 2.“地震无情人有情”，雅安地震牵动了全国人民的心．某地震救援队探测出某建筑物废墟下方点 处有 生命迹象，已知废墟一侧地面上探测点 、 相距 2 ，探测线与地面的夹角分别是 30º和 60º，试确定 生命所在点 的深度．（结果保留到 0.1 ） [来源:Zxxk.Com] 3.为方便市民低碳生活绿色出行，市政府计划改造如图所示的人行天桥：天桥的高是 10 米，原坡面倾斜 角∠CAB=45°． （1）若新坡面倾斜角∠CDB=28°，则新坡面的长 CD 长是多少？（精确到 0.1 米） （2）若新坡角顶点 D 前留 3 米的人行道，要使离原坡角顶点 A 处 10 米的建筑物不拆除，新坡面的倾 斜角∠CDB 度数的最小值是多少 ？（精确到 1°） 4．如图，小明在大楼 30 米高（即 PH＝30 米）的窗口 P 处进行观测，测得山坡上 A 处的俯角为 15°，山脚 B 处的俯角为 60°，已知该山坡的坡度 i（即 tan∠ABC）为 1： 3 ，点 P、H、B、C、A 在同一个平面上．点 H、B、C 在同一条直线上，且 PH⊥HC． （1）山坡坡角（即∠ABC）的度数等于_***_度； （2）求 A、B 两点间的距离（结果精确到 0.1 米）． 第 2 题图 第 3 题 解直角三角形 12 5．目前世界上最高的电视塔是广州新电视塔．如图 8 所示，新电视塔高 AB 为 610 米，远处有一栋大楼， 某人在楼底 C 处测得塔顶 B 的仰角为 45°，在楼顶 D 处测得塔顶 B 的仰角为 39°．（1）求大楼与电视塔 之间的距离 AC； （2）求大楼的高度 CD（精确到 1 米） 45° 39°D C A E B 参考答案： 热点聚焦﹒考点突破 【例 1】解析：1、由题目可知道，气球的高度就是 CD 的长加上小明的眼睛离地面 1.6m． 2、假设 CD 为 h m，BD 为 x m，在 Rt△ADC 和 Rt△BDC 利用正弦列出两个方程求出. 解答：设 CD 为 h m，BD 为 x m， 在 Rt△ADC 中， tan3050 h x   ① 在 Rt△BDC 中， tan 45h x   ② 整理①、②得方程： 3 3 （x+50）=x 解得：h=x= 50 3 1 ≈68.31 68.31+1.6=69.91(米) 答：气球的高度约为 69.91 米。 解直角三角形 13 【例 2】作 DF⊥AB 于 F 点． 在 Rt△DEF 中，设 EF=x，则 DF= 3 x． 在 Rt△ADF 中，tan50°= 30 3 x x  ≈1.20， ∴30+x= 3x ×1.20， x≈27.8， ∴DF= 3 x≈48． 答：张明同学站在离办公楼约 48 米处进行测量的． 【变式训练 1】 【难度分级】 B 1．如图，过点 A 作 AD⊥BC，垂足为 D． 根据题意，可得∠BAD=60°，∠CAD=30°，AD=60 在 Rt△ADB 中，BD=AD×tan60°=60 3 (m)， 在 Rt△ADC 中，CD=AD×tan30°=20 3 (m)， ∴BC=CD+BD=60 3 +20 3 =80 3 ≈138.4（m）． 答：这栋楼高约为 138.4m． 2．根据题意：在 Rt△ABD 中，有 BD=AD•tan52°． 在 Rt△ADC 中，有 DC=AD•tan35°． 则有 BC=BD-CD=6（1.28-0.70）=3.5（米）． 3．由 C 点向 AB 作垂线，交 AB 的延长线于 E 点，并交海面于 F 点． 已知 AB=4000（米），∠BAC=30°，∠EBC=60°， ∵∠BCA=∠EBC—∠BAC=30°， ∴∠BAC=∠BCA． ∴BC=BA=4000（米）． 在 Rt△BEC 中， EC=BC•sin60°=4000× 3 2 =2000 3 （米）． ∴CF=CE+BF=2000 3 +500≈3964（米）． 答：海底黑匣子 C 点处距离海面的深度约为 3964 米． 【例 3】解析：如果延长 BC 交 AD 于 E 点，则 CE⊥AD，要求 BC 的高度，就要知道 BE 和 CE 的高度，就要 先求出 AE 的长度．直角三角形 ACE 中有坡比，由 AC 的长，那么就可求出 AE 的长，然后求出 BE、CE 的高 度，BC=BE—CE，即可得出结果． 解直角三角形 14 解答：延长 BC 交 AD 于 E 点，则 CE⊥AD． 在 Rt△AEC 中，AC=10，由坡比为 1： 3 可知：∠CAE=30°， ∴CE=AC•sin30°=10× 1 2 =5， AE=AC•cos30°=10× 3 2 =5 3 ． 在 Rt△ABE 中，BE= 2 2AB AE = 2 214 (5 3) =11． ∵BE=BC+CE，∴BC=BE-CE=11-5=6（米）． 答：旗杆的高度为 6 米． 【例 4】 解析：应把所求的 HD 进行合理分割=HN+NF+FD，可利用 Rt△MHN 和 Rt△EFD 中的三角函数来做． 解答：∵BG=3.2m， ∴加高后 MN=EF=5.2m，ME=NF=6m， 在 Rt△HMN 和 Rt△DEF 中， MN HN = 1 2.5 ， EF DF = 1 2 ， ∴HN=2.5MN=13m，DF=2EF=10.4m，HD=13+6+10.4=29.4m． 答：加高后的坝底 HD 的长为 29.4m。 【变式训练 2】 【难度分级】 B 1．如图，延长 AD 交 BC 的延长线于点 F，过点 D 作 DE⊥BC 的延长线与点 E． ∵∠DCE=30°，CD=8， ∴CE=CD•cos∠DCE=8× 3 2 =4 3 ， ∴DE=4， 设 AB=x，EF=y， ∵DE⊥BF，AB⊥BF， ∴△DEF∽△ABF， ∴ DE AB = EF BF ，即 4 x = 20 4 3 y y  …①， ∵1 米杆的影长为 2 米，根据同一时间物高与影长成正比可得， 1 2 = 20 4 3 x y  …②， ①、②联立，解得 x=14+2 3 （米）． 故答案为：14+2 3 ． 2．（1）由题意 AB= 2 2AC BC =2 5 ≈4.5m，因此滑梯的长约为 4.5m． 解直角三角形 15 （2）Rt△ABC 中，AC：BC=1：2， ∴tan∠ABC= 1 2 ． ∴锐角∠ABC≈27°＜45°． 这架滑梯的倾斜角符合要求． 3．分别作 DM⊥AB 交 AB 于 M，EN⊥AB 交 AB 于 N． ∵ DM AM = 1 1 ，∴∠DAM=45 度． ∵AD=8，∴DM=AM=4 2 ． 又∵CD∥AB，∴EN=DM=4 2 ， DE=MN=1.6． 在 Rt△FNE 中， EN FN = 1 2 ， ∴FN=2EN=8 2 ． ∴FA=FN+NM-AM=8 2 +1.6—4 2 =4 2 +1.6≈7.26． S 四边形 ADEF= 1 2 （AF+DE）•EN= 1 2 （7.26+1.6）×5.66≈25.07（m2）． V 体积=S 四边形 ADEF×96=25.07×96=2.4×103（m3）． 答：完成这一工程需 2.4×103m3 的土方． 【例 5】解析：由已知可得△ABC 中∠BAC=30°，∠BCA=45°且 AB=10 海里．要求 BC 的长，可以过 B 作 BD ⊥AC 于 D，先求出 AD 和 CD 的长．转化为运用三角函数解直角三角形． 解答：如图，过 B 点作 BD⊥AC 于 D． ∴∠DAB=90°—60°=30°，∠DCB=90°—45°=45°． 设 BD=x，在 Rt△ABD 中，AD= tan30 x  = 3 x， 在 Rt△BDC 中，BD=DC=x，BC= 2 x， ∵AC=5×2=10， ∴ 3 x+x=10． 得 x=5（ 3 —1）． ∴BC= 2 •5（ 3 —1）=5（ 6 2 ）（海里）． 答：灯塔 B 距 C 处 5（ 6 2 ）海里 【变式训练 3】 【难度分级】 B 答案： 1．（1）设 CE 交 AB 于 O，由题意知：∠A=60°，∠AOC=30°。 解直角三角形 16 故：AO=2AD=4；OB=10-AO=6。 ∵∠BOE=∠AOC=30° ∴BE= 1 2 OB=3（km) （2）由勾股定理可求：OE=3 3 。 tan∠CBE= CE BE ，即 tan76°= 3 CE ，CE=12.03（km） 则：CO=CE-OE=12.03—3 3 =6.84（km） 在△ADO 中，同理可求：DO=2 3 =3.46（km） CD=CO-DO=6.84—3.46=3.38（km） 5min= 1 12 h 轮船的速度为：3.380÷（ 1 12 ）≈40.1（km/h） 2．不会穿过居民区． ∵∠EBN=∠FMN=30°，∠ABE=75°， ∴∠ABN=∠ABE-∠EBN=75°—30°=45°， 过 A 作 AH⊥MN 于 H，则∠ABH=45°，AH=BH 设 AH=x，则 BH=x，MH= 3 x=x+400 ∴x=200 3 +200=546.1＞500 ∴不会穿过居民区． 3．（1）该城市会受到这次台风的影响． 理由是：如图，过 A 作 AD⊥BC 于 D．在 Rt△ABD 中， ∵∠ABD=30°，AB=220， ∴AD= 1 2 AB=110， ∴受台风影响范围的半径为 20×（12—4）=160． ∵110＜160， ∴该城市会受到这次台风的影响． （2）如图以 A 为圆心，160 为半径作⊙A 交 BC 于 E、F． 则 AE=AF=160． ∴台风影响该市持续的路程为：EF=2DE=2 2 2160 110 =60 15 ． ∴台风影响该市的持续时间 t= 60 15 15 =4 15 （小时）． （3）∵AD 距台风中心最近， ∴该城市受到这次台风最大风力为：12—（110÷20）=6.5（级）． 解直角三角形 17 专题训练﹒对接中考 1.解：设小山岗的高 AB 为 x 米．……… 1 分 依题意，得在 Rt ABC△ 中， 3tan 4 AB x BC BC     ， 4 3BC x  .……… 3 分 4200 3BD DC BC x     . ……… 4 分 在 Rt ABD△ 中， tan ABADB BD ∠ ， tan 26.6 0.50 ， 0.504200 3 x x    . ……… 7 分 解得 300x  . ……… 9 分 经检验， 300x  是原方程的解. ……… 11 分 答：小山岗的高 AB 为 300 米. ………… 12 分 2．（2015 年黄埔一模） （1）如图所作 DC 为所求……4 分（图略） （2）∵∠DBC=62°, ∠DAB=31° ∴∠BDA=∠DAB=31° ∴AB=DB ∵AB=140（米）， ∴DB=140（米）. 在 Rt△DCB 中，∠C=90°， DB DCDBC sin ∴ 12462sin140 DC （米） ……10 分 答：略 3.（本题满分 10 分） 解：由题可得， ABD=90 60 , 40ADB ACB       ， （1）在 RT△ABD 中， ABD=90  tan ABADB BD   ―――――――3 分 60tan 60 BD   第 20 题 图① 图② 31 A D 62 B 解直角三角形 18 ∴ 60 =20 3tan 60BD   答：BD 的长为 20 3 米。 ――――――――――5 分 （2）在 RT△ABC 中， ABD=90  tan ABACB BC   ――――――――――――7 分 tan40°= BC 60 ∴ 60 =71.51tan 40BC   ―――――――――――8 分 CD=CB-BD=36.87≈36.9(米) 答：河宽大约为 36.9 米―――――――――――――10 分 4.（2016 年广州中考.22,12 分） 解：（1）∵∠BAC=90°-30°=60°，AC=60m ∴在 Rt△ABC 中，有 mBAC ACAB 12060cos 60 cos  （2）作 DE⊥ ，AA 于点 E，连结 DA， ∵∠DAC=90°-60°=30°，AC=60m ∴在 Rt△ADC 中，有 CD=AC×tan∠DAC=60×tan30°= 320 m ∵∠AED=∠EAC=∠C=90° ∴四边形 ACDE 是矩形。 ∵ED=AC=60m，EA=CD= 320 m ∴在 Rt△ EDA， 中，有 5 32 330320 60tan ,, ,      AAEA ED EA EDDEA 解直角三角形 19 即从无人机 ，A 上看目标 D 俯角正切值为 5 32 。 5.（2013 年广州市中考.22，12 分）解：（1）如图，过点 P 作 PH⊥MN 于点 H, ∵船 P 在船 A 的北偏东 58°方向，∴∠PAH=320。 ∵AP=30 海里， ∴ （海里）。 答：船 P 到海岸线 MN 的距离为 15.9 海里。 （2）∵船 P 在船 B 的北偏西 35°方向，∴∠PBH=550。 ∴ （海里）。 ∵船 A、船 B 的速度分别为 20 海里/小时、15 海里/小时， ∴船 A 到达船 P 的时间为 （小时），船 B 到达船 P 的时间为 （小时）。 ∵ ，∴船 B 先到达船 P。 （1）过点 P 作 PH⊥MN 于点 H,构造直角三角形 PAH，应用正弦函数即可求得船 P 到海岸线 MN 的距离 PH。 （2 分别求出两船 A 到达船 P 的时间进行比较即可得出结论。 作业： 一．选择题。 1．D 解直角三角形 20 二、填空题。 1．16 3 2.58.57m 3. 20 2 三．解答题： 1.（2013 年从化一模.22.12 分）解：过点 B 作 BE⊥CD，连结 BC， 则∠α=60°，∠β=30°，------------------------1 分 ∵四边形 ABEC 是平行四边形 ∴BE=AC=50，AB=CE---------------------------------3 分 在 Rt△BCE 中， ∵tanα= CE BE ∴ tanCE BE  α=50 3 =50 3 --------------------6 分 ∴AB=50 3 ≈86.6(米) ----------------------------7 分 在 Rt△BDE 中， ∵tanβ= DE BE ∴ tanDE BE  β=50 3 3  = 50 3 3 -----------------------10 分 ∴CD=CE+DE=50 3 + 50 3 3 ≈115.5（米）------------------------11 分 答：建筑物 AB 的高度约为 86.6 米，建筑物 CD 的高度约为 115.5 米. --------------12 分 2.（2012 年海珠区二模 20）（本题满分 10 分） 解：如图：过点 C 作 CD⊥AB，垂足为 D，依题意： ∵∠1=60°，∠2=30°，AB=2m ∴∠DBC=∠1=60°，∠BAC=∠2=30° ∴∠BCA=∠DBC-∠BAC=30°=∠BAC ∴BC= AB=2m ∴CD= = ≈1.7m 即：生命所在点 C 的深度约为 1.7m 3.（2013 年黄埔一模 22）（1）∵ CD CBCDB sin 第 20 题图 第 22 题 解直角三角形 21 ∴ 3.21sin28 10 sin  CDB CBCD ……5 分 答：新坡面的长为 21.3 米 （2）∵∠CAB=45°，∴AB=CB=10， ……6 分 又建筑物离原坡角顶点 A 处 10 米，即建筑物离天桥底点 B 的距离为 20 米，……7 分 当 DB 取最大值时， CDB 达最小值， 要使建筑物不被拆掉 DB 的最大值为 20-3=17 ……8 分 又 17 10tan  DB CBCDB ，  31CDB ……12 分 答，若新坡角顶点 D 前留 3 米的人行道，要使离原坡角顶点 A 处 10 米的建筑物不拆除，新坡面的倾斜角 的最小值是 31° 4.（2013 年广雅一模 20）解：（1）30 （2）由题意得：∠PBH＝60°∠APB＝45°∵∠ABC＝30°∴∠ABP＝90° 在 Rt△PHB 中， ,320sin  PBH PHPB 在 Rt△PBA 中，AP＝ 6.34320sin  PBH PHPB 答：A、B 两点间距离约 34.6 米。 5．（2010 广州中考，22，12 分） 【分析】（1）由于∠ACB＝45°，∠A＝90°，因此△ABC 是等腰直角三角形，所以 AC＝AB＝610；（2） 根据矩形的对边相等可知：DE＝AC＝610 米，在 Rt△BDE 中，运用直角三角形的边角关系即可求出 BE 的长， 用 AB 的长减去 BE 的长度即可． 【答案】（1）由题意，AC＝AB＝610（米）； （2）DE＝AC＝610（米），在 Rt△BDE 中，tan∠BDE＝ BE DE ，故 BE＝DEtan39°． 因为 CD＝AE，所以 CD＝AB－DE·tan39°＝610－610×tan39°≈116（米） 答：大楼的高度 CD 约为 116 米．