北京市西城区2007年抽样测试

北京市西城区2007年抽样测试

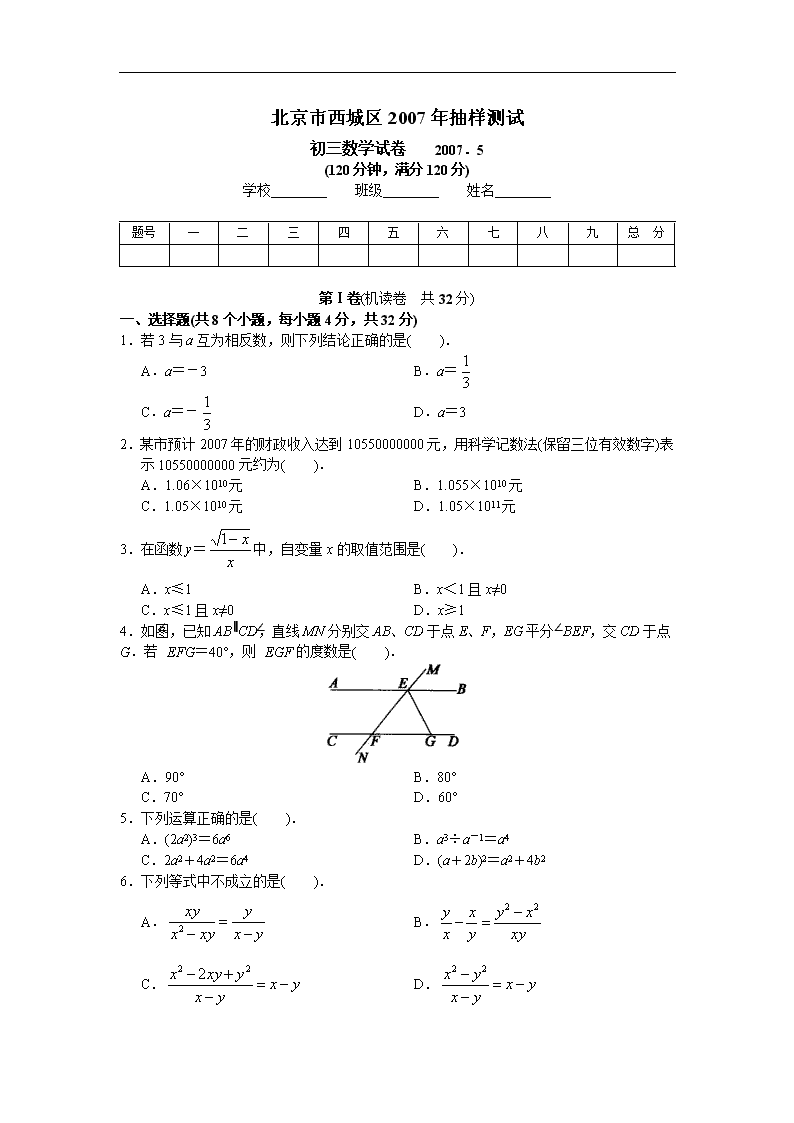
北京市西城区2007年抽样测试 初三数学试卷 2007．5‎ ‎(120分钟，满分120分)‎ 学校________ 班级________ 姓名________‎ 题号 一 二 三 四 五 六 七 八 九 总 分 第Ⅰ卷(机读卷 共32分)‎ 一、选择题(共8个小题，每小题4分，共32分)‎ ‎1．若3与a互为相反数，则下列结论正确的是( )．‎ A．a＝－3 B．a＝‎ C．a＝－ D．a＝3‎ ‎2．某市预计2007年的财政收入达到10550000000元，用科学记数法(保留三位有效数字)表示10550000000元约为( )．‎ A．1.06×1010元 B．1.055×1010元 C．1.05×1010元 D．1.05×1011元 ‎3．在函数y＝中，自变量x的取值范围是( )．‎ A．x≤1 B．x＜1且x≠0‎ C．x≤1且x≠0 D．x≥1‎ ‎4．如图，已知AB∥CD，直线MN分别交AB、CD于点E、F，EG平分∠BEF，交CD于点G．若∠EFG＝40°，则∠EGF的度数是( )．‎ A．90° B．80°‎ C．70° D．60°‎ ‎5．下列运算正确的是( )．‎ A．(‎2a2)3＝‎6a6 B．a3÷a－1＝a4‎ C．‎2a2＋‎4a2＝‎6a4 D．(a＋2b)2＝a2＋4b2‎ ‎6．下列等式中不成立的是( )．‎ A． B．‎ C． D．‎ ‎7．数学老师对小方中考前的6次模拟考试成绩进行了统计分析，判断小方的数学成绩是否稳定，于是数学老师需要知道小方这6次数学成绩的( )．‎ A．平均数 B．众数 C．频数 D．方差 ‎8．一个正方体的展开图如右图所示，每一个面上都写有一个自然数并且相对两个面所写的两个数之和相等，那么a＋b－‎2c＝( )．‎ A．40 B．38‎ C．36 D．34‎ ‎第Ⅱ卷(非机读卷 共88分)‎ 二、填空题(共4个小题，每小题4分，共16分)‎ ‎9．分解因式m3－‎9m＝________．‎ ‎10．在一个口袋中装有若干个只有颜色不同的球，如果口袋中装有四个红球，且摸出红球的概率为，那么袋中共有________个球．‎ ‎11．△ABC中，∠A＝70°，若O为△ABC的外心，则∠BOC＝________．‎ ‎12．如图，在△ABC中，∠C＝90°，点O在AB上，且AC，BC分别与圆O相切于点M、N，若AO＝‎15厘米，OB＝20厘米，则圆O的面积为________平方厘米．‎ 三、解答题(本题共30分，每小题5分)‎ ‎13．计算：(tan60°)2＋－(2007－)0＋()－2．‎ ‎14．解不等式：‎ ‎15．已知关于x的方程2x2－mx＋3＝0的一个解是1，求m的值和该方程的另一个解．‎ ‎16．如图，正方形ABCD的边长为1，点P为BC边上的任意一点(可与点B或C重合)，分别过B、D作AP的垂线段，垂足分别是B1、D1．猜想：(DD1)2＋(BB1)2的值，并对你的猜想加以证明．‎ ‎17．已知：x＝－1，求的值．‎ ‎18．如图，在△ABC中，∠C＝90°，D、E在BC上，BD＝DE＝EC＝AC，指出图中哪两个三角形相似，并证明你的结论．‎ 四、解答题(本题共20分，第19题6分，第20题5分，第21题5分，第22题4分)‎ ‎19．如图，圆O的半径OA与OB互相垂直，P是线段OB延长线上的一动点，线段AP交圆O于点D，过D点作圆O的切线交OP于点E．‎ ‎(1)观察图形，点P在移动过程中比较DE与EP的大小关系，并对你的结论加以证明；‎ ‎(2)作DH⊥OP于点H，若HE＝6，DE＝4，求圆O半径的长．‎ ‎20．商场对消费每满200元的顾客有两种促销方式供经理选择：‎ 第一种是顾客在商场消费每满200元就有一次摸奖的机会，即从一个装有100个大小相同的乒乓球(球上分别写有1、2、3、……，100这100个数字)的箱子中摸出一个球(摸后放回)，若球上的数字是88，则送价值800元的商品，如果是33或66或99，则送价值300元的商品，若球上的数字能被5整除，则送价值50元的商品，其他数字不送商品．‎ 第二种是顾客在商场消费每满200元直接送价值30元的商品．‎ 估计活动期间将有8000人次参加促销活动，请你运用所学的概率知识分析一下．‎ ‎(1)摸奖获得价值分别为800元、300元、50元商品的概率各是多少?‎ ‎(2)商场经理应选择哪种促销方式投入资金可能更少?‎ ‎21．已知点A是正比例函数y＝2x的图象与反比例函数y＝图象在第三象限的交点．‎ ‎(1)如果直线y＝x＋b经过点A且与x轴交于点C，求b的值和C点坐标；‎ ‎(2)在x轴上确定点B，使△ACB的面积等于10．‎ ‎22．玩具厂新出一套模板，它是由2个小正方形，5个大小不都全等的等腰直角三角形组成，拼成如右图所示的正方形．‎ ‎(1)请用上述模板拼出一个直角梯形，并用三角尺和圆规按1：1画出它们的拼接图形；‎ ‎(2)如右图，若正方形ABCD的面积为16，求△HED的面积(直接写出结果，不要求计算过程)．‎ 五、解答题(本题共22分，第23题6分，第24题8分，第25题8分)‎ ‎23．农科所有一块五边形的实验田，用于种植1号良种水稻进行实验，如图所示，已知五边形ABCDE中，∠ABC＝∠AED＝90°，AB＝CD＝AE＝BC＋DE＝‎20米，‎ ‎(1)若每平方米实验田需要水稻1号良种‎25克，若在△ABC和△ADE实验田中种植1号良种水稻，问共需水稻1号良种多少克?‎ ‎(2)在该五边形实验田计划全部种上这种1号良种水稻，现有1号良种‎9千克，问是否够用，通过计算加以说明．‎ ‎24．如图，在直角坐标系xoy中，点A在x轴的正半轴上，点C在y轴上，且OC＝，tan∠OAC＝，将△OAC沿AC翻折使点O落在坐标平面内的B点处．‎ ‎(1)求B点的坐标；‎ ‎(2)二次函数y＝ax2＋bx＋c的图象经过O、B、A三点，求这个二次函数的解析式；‎ ‎(3)在(2)中的二次函数图象上是否存在一点P，使以P、A、B、O为顶点的四边形为梯形?若存在，求出P点坐标，若不存在，说明理由．‎ ‎25．我们给出如下定义：三角形三条中线的交点称为三角形的重心．一个三角形有且只有一个重心．可以证明三角形的重心与顶点的距离等于它与对边中点的距离的两倍．‎ 可以根据上述三角形重心的定义及性质知识解答下列问题：‎ 如图，∠B的平分线BE与BC边上的中线AD互相垂直，并且BE＝AD＝4，‎ ‎(1)猜想AG与GD的数量关系，并说明理由；‎ ‎(2)求△ABC的三边长．‎ 北京市西城2007年抽样测试 数学评分标准及参考答案 2007．5‎ 一、选择题(共8个小题，每小题4分，共32分)‎ 题号 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ 答案 A A C C B D D B 二、填空题(共4个小题，每小题4分，共16分)‎ ‎9．m(m＋3)(m－3)； 10．12； 11．140； 12．144π 三、解答题(本题共30分，每小题5分)‎ ‎13．解：‎ ‎＝……………………………………………………………3分 ‎＝ ……………………………………………………………………4分 ‎＝…………………………………………………………………………5分 ‎14．解：‎ 解(1)得，x＞－1，………………………………2分 解(2)得，x≤1．…………………………………4分 所以－1＜x≤1． ………………………………5分 ‎15．解：由于1是方程2x2－mx＋3＝0的一个解，所以将x＝1代入该方程，得m＝5．‎ ‎ ………………………………………………………………………………………2分 将m＝5，代入方程2x2－mx＋3＝0中，得2x2－5x＋3＝0．‎ 即，(2x－3)(x－1)＝0，‎ 解得，，x2＝1．……………………………………………………………4分 答：m＝5，原方程的另一个解是．‎ ‎16．解：猜想：(DD1)2＋(BB1)2的值是1．………………………………………………1分 证明如下：在△ADD1和△ABB1中，‎ ‎∵四边形ABCD是正方形，‎ ‎∴AD＝AB．‎ ‎∵AD1⊥DD1，BB1⊥AB1，‎ ‎∴∠DD‎1A ＝∠AB1B＝90°. ………………………………………………………2分 ‎∵∠DAD1＋∠B1AB＝∠B1AB＋∠ABB1‎ ‎∴∠DAD1＝∠ABB1．………………………………………………………………3分 ‎∴△ADD1≌△BAB1．………………………………………………………………4分 ‎∴AD1＝BB1．‎ ‎∵(DD1)2＋(BB1)2＝(DD1)2＋(AD1)2＝AD2＝1‎ ‎∴(DD1)2＋(BB1)2＝1．………………………………………………………………5分 ‎17．解：‎ ‎……………………………………………………………1分 ‎．………………………………………………………………………………3分 将x＝－1代入，得 原式……………………………………………………………5分 ‎18．解：△AED∽△BEA．‎ 证明如下：在△AED和△BEA中，‎ ‎∵△ABC中，∠C＝90°，BD＝DE＝EC＝AC，‎ ‎∴AE＝AC，BE＝‎2AC．‎ ‎………………………………………………………………………3分 ‎∵∠AED＝∠BEA, ………………………………………………………………………4分 ‎∴△AED∽△BEA. ………………………………………………………………………5分 四、解答题(本题共20分，第19题6分，第20题5分，第21题5分，第22题4分)‎ ‎19．(1)DE＝EP．………………………………………………………………………………1分 证明如下：连接OD．因为EF是⊙O 的切线，所以OD⊥EF．‎ ‎∵OA＝OD,‎ ‎∴∠OAP＝∠ODA.‎ ‎∴∠EDP＝∠ADF＝90°－∠ODA＝90°－∠OAP.‎ ‎∵AO⊥OP,‎ ‎∴∠P＝90°－∠OAP．‎ ‎∴∠P＝∠EDP．………………………………………………………………………2分 ‎∴DE＝EP．……………………………………………………………………………3分 ‎(2)在Rt△DHE中，∵HE＝6，DE＝4，∠DHE＝90°，‎ ‎∴cos∠HED＝＝，有∠HED＝30°．‎ ‎∴∠DOB＝60°．………………………………………………………………………4分 ‎∵△ODE是直角三角形，DE＝4．‎ ‎∴OD＝4．………………………………………………………………………………6分 ‎20．解：(1)获得价值800元商品的概率是0.01，…………………………………………1分 获得价值300元商品的概率是0.03，……………………………………………2分 获得价值50元商品的概率是0.2．………………………………………………3分 ‎(2)如果有8000人次参加摸球，那么相应的频率大致为0.01，0.03，0.2．商场送了同的商品的金额估计是：‎ ‎8000×(0.01×800＋0.03×300＋0.2×50)＝216000元．‎ 如果有8000人次直接获得商品，需付出商品的金额为8000×30＝240000元．‎ ‎……………………………………………………………………………………4分 因为240000＞216000，‎ 所以商场经理选择摸球的促销方式投资可能较少．……………………………5分 ‎21．解：(1)已知点A是正比例函数y＝2x的图像与反比例函数y＝图像在第三象限的交点．‎ 所以解方程组，得x＝±2．……………………………………………1分 由于A点在第三象限，所以A(－2，－4)．‎ 由于直线y＝＋b过A点，有－4＝×(－2)＋b，所以b＝－.………2分 由于直线y＝－与x轴的交点是C，所以C(1，0)．……………………3分 ‎(2)由于S△ACB＝10，所以|xB－1|×4＝10，所以|xB－1|＝5． ………………4分 解得xB＝－4或xB＝6，所以B点的坐标是B1(－4，0)，B2(6，0)．………5分 ‎22．(1)‎ ‎ 或 ‎ 说明：答案不唯一，正确画出一个符合要求的图即可给2分．‎ ‎(2)因为正方形的边长是4，所以△HED的面积是1．………………………………4分 五、解答题(本题共22分，第23题6分，第24题8分，第25题8分)‎ ‎23．(1)∵AB＝AE＝BC＋DE＝‎20米．‎ 又 ‎＝×20×20＝200(平方米)‎ ‎∴所需1号良种数是：25×200＝5000(克)．……………………………………………2分 ‎(2)把△AED，以A点为旋转中心逆时针旋转，‎ 使AE与AB重合，有△ADE与△全等．‎ ‎∵∠ABC＝∠AED＝90°，‎ ‎∴C、B、三点共线．………………………………………………………………3分 在△ACD和△中，‎ ‎∵AD＝AD′，AC＝AC，BC＋BD′＝CD′＝CD．‎ ‎∴△ACD≌△ACD′‎ 由(1)知S△ABC＋S△ADE＝200(平方米)‎ ‎∴五边形ABCDE的面积＝2(S△ABC＋S△ADE)＝400(平方米)．‎ ‎∵每平方米需要1号良种‎25克，‎ ‎∴若五边形ABCDE实验田全部种上1号良种，共需1号良种25×400＝‎10000克＝‎10千克．‎ ‎∵9＜10．‎ ‎∴五边形ABCDE实验田全部种上1号良种实现不了．……………………………6分 ‎24．(1)∵tan∠OAC＝，∴有∠OAC＝30°．‎ ‎∴，OA＝4．……………………………………………………………1分 由△OAC沿AC翻折知，OB⊥AC，所以∠BOA＝60°，∠OAB＝2∠OAC＝60°，知△OAB是等边三角形．‎ 所以OB＝OA＝4．‎ 因为xB＝OBcos∠BOA＝2，yB＝OBsin∠BOA＝2，‎ 所以，即B(2，2)．………………………………………………2分 ‎(2)因为二次函数y＝ax2＋bx＋c的图象经过O、B、A三点，‎ 所以设其为y＝ax2＋bx．‎ 因为A(4，0)，B(2，2)，将其代入，得 得所以……………………4分 说明：用其它方法正确得到解析式，同样给分．‎ ‎(3)若存在点P使四边形PABO为梯形．‎ 因为B为抛物线顶点，所以OA不可能为梯形的底．‎ ‎1．当OB∥P‎1A时，有∠OAD＝60°．‎ 设AP1交y轴于点D，因为OA＝4，所以D(0，－4)．‎ 设过A、D的直线解析式为y＝kx＋b(k≠0)，‎ 所以有得y＝x－4．‎ 因为P1是二次函数图象与直线AD的交点 所以 解出 或 因为A(4，0)，所以P1(－2，－6)．………………………………………6分 过P1作PM⊥x轴于M点，则线段P‎1M＝6.‎ 所以线段P‎1A＝12，OB＝4．‎ 在四边形P1ABO中，BO∥AP1，且BO≠AP1，所以四边形P1ABO是梯形．‎ ‎ …………………………………………………………………………………7分 ‎2．当OP2∥BA时，同理可求出另一个点P2(6，－6)．………………………8分 说明：只要正确说明一组对边不平行的理由给1分．‎ ‎25．解1：(1)AG＝GD．……………………………………………………………………1分 ‎∵BE平分∠B，‎ ‎∴∠ABG＝∠DBG．‎ ‎∵BG⊥AD，BG＝BG．‎ ‎∴∠BGA＝∠BGD，‎ ‎∴△ABG≌△DBG，‎ ‎∴AG＝GD，AB＝BD．……………………………………………………………2分 ‎(2)延长BA到F，使AF＝BA，‎ ‎∴△BFC是等腰三角形．…………………………………………………………4分 ‎∵AD是BC的中线，‎ ‎∴AD是△BFC的一条中位线．‎ 延长BE交CF于H点，则BH垂直平分FC．‎ ‎∴E是△BFC的重点．……………………………………………………………5分 ‎∴在Rt△BHC中，…………………6分 ‎…………………………………………………………7分 ‎∵在Rt△EHC中，‎ ‎∴AC＝AE＋EC＝3．…………………………………………………………8分 解2：(1)AG＝GD．‎ ‎∵BE平分∠B，‎ ‎∴∠ABG＝∠DBG．‎ ‎∵BG⊥AD，BG＝BG．‎ ‎∴∠BGA＝∠BGD，‎ ‎∴△ABG≌△DBG，‎ ‎∴AG＝GD．…………………………………………………………………………2分 ‎(2)从点C作CH∥AD与BE的延长线交于H．…………………………………3分 ‎∵GD∥HC，‎ ‎∴△BGD∽△BHC．‎ 有D是BC的中点，G是AD的中点，也是BH的中点 ‎∵GD＝2．‎ ‎∴HC＝4．BG＝GH.‎ 设BG＝x，则 GE＝4－x，EH＝2x－4，‎ ‎∵AG∥HC，‎ ‎∴△AGE∽△CHE．‎ 即 解出，x＝3．………………………………………………………………………5分 ‎∴在Rt△BHC中，………………6分 ‎…………………………………………………………7分 ‎∵GE＝1，EH＝2，‎ ‎∴在Rt△AGE中， ‎ ‎∵EC＝2AE＝2．‎ ‎∴AC＝3．………………………………………………………………………8分