- 2021-11-10 发布 |
- 37.5 KB |
- 66页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
江西专版2020中考数学复习方案第三单元函数第11课时反比例函数课件
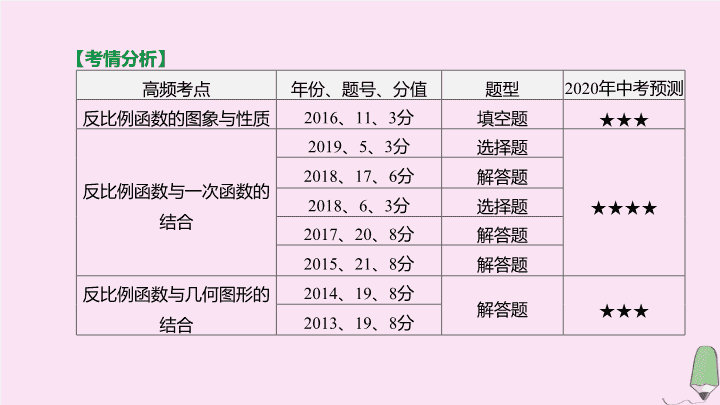
第 11 课时 反比例函数 第三单元 函数 【 考情分析 】 高频考点 年份、题号、分值 题型 2020 年中考预测 反比例函数 的图象 与性质 2016 、 11 、 3 分 填空题 ★★★ 反比例函数 与一次函数的结合 2019 、 5 、 3 分 选择题 ★★★★ 2018 、 17 、 6 分 解答题 2018 、 6 、 3 分 选择题 2017 、 20 、 8 分 解答题 2015 、 21 、 8 分 解答题 反比例函数 与几何图形 的结合 2014 、 19 、 8 分 解答题 ★★★ 2013 、 19 、 8 分 考点一 反比例函数的概念 考点聚焦 【 温馨提示 】 (1) 反比例函数中 , 自变量的取值范围是 ① ; (2) 解析式的变式 : y=kx -1 或 xy=k ( k ≠0) . x ≠0 考点二 反比例函数的图象与性质 > < 减小 增大 对称性 关于直线 y=x , y= - x 成轴对称 关于 ⑥ 成中心对称 小结 (1) 反比例函数的图象是双曲线 , 反比例函数的增减性由系数 k 决定 ; (2) 反比例函数图象的两支在两个象限内 , 根据自变量的值比较相应函数值的大小时 , 应注意象限问题 (续表) 原点 考点三 反比例函数比例系数 k 的几何意义 2. 常见的与反比例函数有关的图形面积 |k| 2 |k| 考点四 反比例函数解析式的确定 利用反比例函数解决实际问题 , 关键是建立函数模型 . 建立函数模型的思路主要有两种 :(1) 已知函数类型 , 直接设出函数的解析式 , 根据题目提供的信息求得 k 的值 ;(2) 题目本身未明确表明变量间的函数关系 , 此时需通过分析 , 先确定变量间的关系 , 再求解析式 . 考点五 反比例函数的实际应用 题组一 必会题 对点演练 A 图 11-1 D B A 图 11-2 B 图 11-3 题组二 易错题 【 失分点 】 对反比例函数中 k 的几何意义理解不到位 ; 反比例函数图象与性质问题中函数的不连续性在研究反比例函数的增减性时要谨慎 . D 图 11-4 < 0查看更多