- 2021-11-06 发布 |
- 37.5 KB |
- 5页

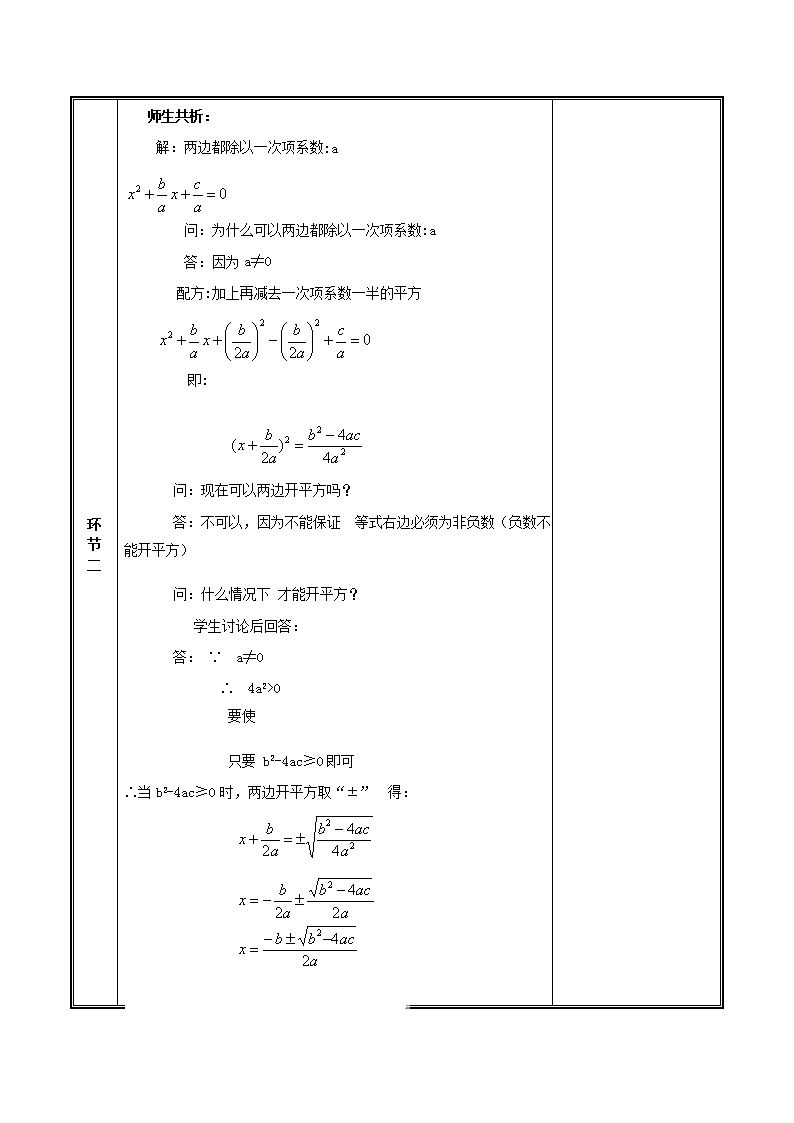

申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2019九年级数学上册 第二章 一元二次方程 3 用公式法求解一元二次方程(第1课时)教案
用公式法求解一元二次方程 课 题 用公式法求解一元二次方程 课时安排 共(2)课时 课程标准 课标P28 能用公式法解数字系数的一元二次方程。 学习目标 1.学生能够正确的导出一元二次方程的求根公式,并在探求过程中培养学生的数学建模意识和合情推理能力; 2.能够根据方程的系数,判断出方程的根的情况,培养学生观察和总结的能力. 3.通过正确、熟练的使用求根公式解一元二次方程,提高学生的综合运算能力. 教学重点 目标1,2 教学难点 目标2, 3 教学方法 支架式教学法,教师引导 教学准备 希沃白板,课件 课前作业 用配方法解下列方程:(1)2x2+3=7x (2)3x2+2x+1=0 全班同学在练习本上运算,可找位同学上黑板演算 教学过程 教学环节 课堂合作交流 二次备课 (修改人: ) 环 节 一 复习回顾: (1)通过课前作业中的两道题进一步夯实用配方法解方程的一般步骤(2)选择了一个没有解的方程,让学生切实感受并不是所有的一元二次方程在实数范围内都有解。 (3)还可以根据上节课作业情况,选学生出错多的题目纠错、练习 课中作业:自主推导求根公式。 提出问题:解一元二次方程:ax2+bx+c=0(a≠0) 环 节 二 师生共析: 解:两边都除以一次项系数:a 问:为什么可以两边都除以一次项系数:a 答:因为a≠0 配方:加上再减去一次项系数一半的平方 即: 问:现在可以两边开平方吗? 答:不可以,因为不能保证 等式右边必须为非负数(负数不能开平方) 问:什么情况下 才能开平方? 学生讨论后回答: 答: ∵ a≠0 ∴ 4a2>0 要使 只要 b2-4ac≥0即可 ∴当b2-4ac≥0时,两边开平方取“±” 得: 问:如果b2-4ac<0时,会出现什么问题? 答:方程无解 如果b2-4ac=0呢?答;方程有两个相等的实数根。 由学生亲身经历公式的推导过程,只有经历了这一过程,他们才能发现问题、汲取教训、总结经验,形成自己的认识.在集体交流的时候,才能有感而发。 活动的实际效果: 学生的主要问题通常出现在这样的几个地方: (1)运算的符号出现错误和通分出现错误 (2)不能主动意识到只有当b2-4ac≥0时,两边才能开平方 (3)两边开平方,忽略取“±”。 大部分学生需要在教师的帮助下,才能完善公式的推导。 (2)活动2:归纳总结公式法定义和根的判别式。 (1)对于一元二次方程:ax2+bx+c=0(a≠0), 当b2-4ac≥0时,;方程有两个实数根 (2)当b2-4ac>0时,方程有两个不相等的实数根; 当b2-4ac=0时,方程有两个相等的实数根; 当b2-4ac<0时,方程没有实数根; (3)根的判别式: 课中作业 巩固新知 1、判断下列方程是否有解:(学生口答) (1) 2x2+3=7x (2)x2-7x=18 (3)3x2+2x+1=0(4)9x2+6x+1=0 (5)16x2+8x=3 (6) 2x2-9x+8=0 学生迅速演算或口算出b2-4ac,从而判断出根的情况。 环 节 三 2、上述方程如果有解,求出方程的解 学生口述,教师板书第(1)题,第(4)题 活动目的:通过让学生或口述交流或上黑板解方程,公示学生的思维过程,查缺补漏,了解学生的掌握情况和灵活运用所学知识的程度。 活动实际效果:教师引导学生分析,学生口答、板书,笔答,对比,评价,总结.大部分学生能够正确、熟练的用公式法解方程。 课堂小结: 1、一元二次方程ax2+bx+c=0(a≠0)的求根公式是什么? 2、如何判断一元二次方程根的情况? 3、用公式法解方程应注意的问题是什么? 4、你在解方程的过程中有哪些小技巧? 课中作业: 课本随堂练习:1,2题 课后作业设计: 1.课本39页习题2.5 1题、2、3题 2.《全品学练考》作业手册 习题2.5 (修改人: ) 板书设计: 2.3用公式法求解一元二次方程 (1)对于一元二次方程:ax2+bx+c=0(a≠0), 当b2-4ac≥0时,;方程有两个实数根 (2)当b2-4ac>0时,方程有两个不相等的实数根; 当b2-4ac=0时,方程有两个相等的实数根; 当b2-4ac<0时,方程没有实数根; (3)根的判别式: 教学反思: 1.要创造性的使用教材 教材只是为教师提供最基本的教学素材,教师完全可以根据学生的实际情况进行适当调整。本节课教师就根据学生实际情况,调整了配方时的个别过程,使之与后续知识学习相一致,添加了例题和练习题。 2.要为学生的终身学习奠基 这节课不能够仅仅让学生背公式、套公式解方程,而应让学生初步建立对一些规律性的问题加以归纳、总结的数学建模意识,亲身体会公式推导的全过程,提高学生推理技能和逻辑思维能力;进一步发展学生合作交流的意识和能力.帮助学生形成积极主动的求知态度.查看更多