人教版九年级数学下册期末测试题及答案

人教版九年级数学下册期末测试题及答案

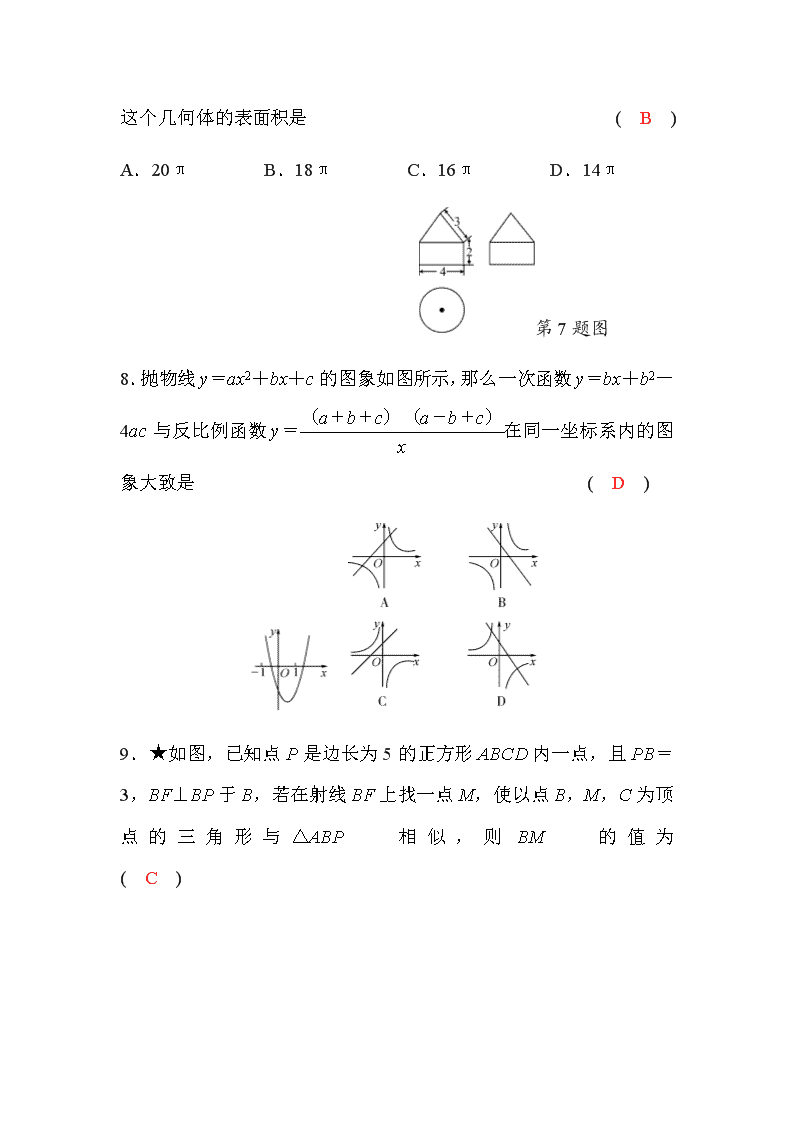
人教版九年级数学下册期末测试题及答案 ‎(考试时间：120分钟　满分：120分)‎ 分数：________‎ 第Ⅰ卷(选择题　共30分)‎ 一、选择题(每小题3分，共30分)　　　　　　　　‎ ‎1．若cos α＝，则锐角α的度数是 (　C　)‎ A．30° B．45° C．60° D．90°‎ ‎2．(上海中考)若反比例函数的图象经过点(2，－4)，则这个反比例函数的解析式是 (　D　)‎ A．y＝ B．y＝－ C．y＝ D．y＝－ ‎3．下列关于投影的说法中不正确的是 (　C　)‎ A．正午，上海中心大厦在地面上的投影是平行投影 B.匡衡借光学习时，他在地面上的投影是中心投影 C.三角形木板的正投影是一个点 D．晚上，小强向路灯走去，他的影子越来越短 ‎4．(绍兴中考)如图，三角板在灯光照射下形成投影，三角板与其投影的相似比为2 ∶5，且三角板的一边长为8 cm，‎ 则投影三角板的对应边长为 (　A　)‎ A．20 cm　 B．10 cm　 C．8 cm　 D．3.2 cm 第4题图 ‎ ‎5．(内江中考)如图，点A是反比例函数y＝图象上的一点，过点A作AC⊥x轴，垂足为点C，D为AC的中点，若△AOD的面积为1，则k的值为 (　D　)‎ 第5题图 A．　 B．　 C．3　　 D．4‎ ‎6．(凉山州中考)如图所示，△ABC的顶点在正方形网格的格点上，则tan A的值为 (　A　)‎ A．　　 B．　 C．2　　 D．22 ‎ 第6题图　　　‎ ‎7．(德阳中考)如图是一个几何体的三视图，‎ 根据图中所示数据计算这个几何体的表面积是 (　B　)‎ A．20π　 B．18π　 C．16π　 D．14π 第7题图 ‎8．抛物线y＝ax2＋bx＋c的图象如图所示，那么一次函数y＝bx＋b2－4ac与反比例函数y＝在同一坐标系内的图象大致是 (　D　)‎ ‎　‎ ‎9．★如图，已知点P是边长为5的正方形ABCD内一点，且PB＝3，BF⊥BP于B，若在射线BF上找一点M，使以点B，M，C为顶点的三角形与△ABP相似，则BM的值为 (　C　)‎ A.3 B． C．3或 D．3或5‎ ‎10．★如图，A，B是反比例函数y＝(k＞0，x＞0)图象上的两点，过点A，B分别作x轴的平行线交y轴于点C，D，直线AB交y轴正半轴于点E.若点B的横坐标为5，CD＝3AC，cos ∠BED＝，则k的值为 (　D　)‎ A．5 B．4 C．3 D． 第10题图 第Ⅱ卷(非选择题　共90分)‎ 二、填空题(每小题3分，共24分)‎ ‎11．已知点A(－2，y1)，B(－1，y2)都在反比例函数y＝－的图象上，则 y1__＜__y2(选填“＞”或“＜”).‎ ‎12．下列几何体中，主视图是三角形的是__②③__．‎ ‎①　　②　　③ ‎ ‎13．(阜新中考)如图，为了了解山坡上两棵树间的水平距离，数学活动小组的同学们测得该山坡的倾斜角α＝20°，两树间的坡面距离AB＝5 m，则这两棵树的水平距离约为__4.7__m(结果精确到0.1 m，参考数据：sin 20°≈0.342，cos 20°≈0.940，tan 20°≈0.364).‎ ‎　第13题图 ‎14．如图，小芳和爸爸正在散步，爸爸身高1.8 m，他在地面上的影长为2.1 m．若小芳比她爸爸矮0.3 m，则她的影长为__1.75__m.‎ 第14题图 ‎15．在△ABC 和△A′B′C′中，∠C＝ ∠C′＝90°，AC＝12，AB＝15，A′C′＝8，当A′B′＝__10__时，△ABC∽△A′B′C′.‎ ‎16．(桂林中考)反比例函数y＝(x＜0)的图象如图所示，关于该函数图象有下列四个结论：①k＞0；②当x＜0时，y随x的增大而增大；③该函数图象关于直线y＝－x对称；④若点(－2，3‎ ‎)在该反比例函数图象上，则点(－1，6)也在该函数的图象上．其中正确结论的个数有__3__个．‎ 第16题图 ‎17．如图，在距离铁轨200 m的B处，观察从南通开往南京的“和谐号”动车，当动车车头在A处时，恰好位于B处的北偏东60°方向上.10 s后，动车车头到达C处，恰好位于B处的西北方向上，则这列动车的平均车速是__20(1＋)__m/s(结果保留根号).‎ 第17题图 ‎18．如图，在平面直角坐标系中，正方形ABCD的面积为20，顶点A在y轴上，顶点C在x轴上，顶点D在双曲线y＝(x>0)的图象上，边CD交y轴于点E，若CE＝ED，则k的值为__4__．‎ ‎　　第18题图 选择、填空题答题卡 一、选择题(每小题3分，共30分)‎ 题号 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ ‎9‎ ‎10‎ 得分 答案 C D C A D A B D C D 二、填空题(每小题3分，共24分)得分：________‎ ‎11．__<__ 12.__②③__ 13．__4.7__ 14.__1.75__‎ ‎15．__10__ 16.__3__ 17．__20(1＋)__ 18.__4__‎ 三、解答题(共66分)‎ ‎19．(6分)计算：tan 45°·sin 60°－＋cos 45°·cos 30°.‎ 解：原式＝1×－＋×＝.‎ ‎20．(8分)在平面直角坐标系中，△OAB三个顶点的坐标分别为O(0，0)，A(3，0)，B(2，3).‎ ‎(1)tan ∠OAB＝__3__；‎ ‎(2)在第一象限内画出△OA′B′，使△OA′B′与△OAB关于点O位似，相似比为2 ∶1；‎ ‎(3)在(2)的条件下，S△OAB ∶S四边形AA′B′B＝__1_∶3__．‎ 解：(2)如图所示，‎ ‎△OA′B′即为所求.‎ ‎(8分)(1)图①是直立在地面上的两根木杆及它们在灯光下的影子，请你在图中画出光源O的位置；‎ ‎(2)太阳光线与地面成60°的角，照射在地面上的一只皮球上，如图②，皮球在地面上的投影长是20 cm，请你求出皮球的半径．‎ 解：(1)如图①所示，点O即为所求．‎ ‎(2)如图②，过点A作AE⊥DB于E，连接CD.由题意，得DC＝2R，AB＝20，∠DBA＝60°，‎ ‎∴DC＝AE＝AB sin 60°＝30(cm).‎ ‎∴皮球的半径为15 cm.‎ ‎22．(8分)如图，在△ABC中，AB＝AC，BC＝10，cos ∠ABC＝，点D是边BC的中点，点E在边AC上，且＝，AD与BE相交于点F.‎ ‎(1)边AB的长为__13__；‎ ‎(2)求的值．‎ 解：过点E作EH∥BC交AD与点H，‎ ‎∵EH∥BC，＝，‎ ‎∴＝＝＝.‎ ‎∵EH∥BC，∴＝＝.‎ ‎23．(10分)如图，大楼AN上悬挂一条幅AB，小颖在坡面D处测得条幅顶部A的仰角为30°，沿坡面向下走到坡脚E处，然后向大楼方向继续行走10米来到C处，测得条幅的底部B的仰角为45°，此时小颖距大楼底端N处20米．已知坡面DE＝20米，山坡的坡度i＝1 ∶‎ ，且D，M，E，C，N，B，A在同一平面内，M，E，C，N在同一条直线上，求条幅AB的长度(结果保留根号).‎ 解：过点D作DH⊥AN于H，‎ 过点E作EF⊥DH于F，‎ ‎∵tan ∠EDF＝tan ∠DEM＝＝1 ∶，‎ ‎∴设EF＝k，则DF＝k，‎ ‎∴k2＋(k)2＝202，∴k＝10，‎ ‎∴EF＝10，DF＝10，‎ ‎∴DH＝DF＋EC＋CN＝10＋30.‎ 在Rt△ADH中，tan ∠ADH＝＝，‎ ‎∴AH＝DH＝10＋10，‎ ‎∴AN＝AH＋EF＝20＋10.‎ ‎∵在Rt△BCN中，∠BCN＝45°，‎ ‎∴CN＝BN＝20，∴AB＝AN－BN＝10.‎ 答：条幅AB的长度是10米．‎ ‎24．(12分)(淄博中考)如图，在直角坐标系中，直线y1＝ax＋b与双曲线y2＝(k≠0)分别相交于第二、四象限内的A(m，4)，B(6，n)两点，与x轴相交于C点，与y轴交于D点．已知OC＝3，tan ∠ACO＝.‎ ‎(1)求y1，y2对应的函数解析式；‎ ‎(2)求△AOB的面积；‎ ‎(3)直接写出当x＜0时，不等式ax＋b＞的解集.‎ 解：(1)∵在Rt△OCD中，OC＝3，tan ∠ACO＝，‎ ‎∴OD＝2，即点D(0，2)，‎ 把点D(0，2)，C(3，0)代入直线y1＝ax＋b，得 b＝2，3a＋b＝0，解得a＝－，‎ ‎∴直线的解析式为y1＝－x＋2.‎ 把A(m，4)，B(6，n)代入y1＝－x＋2，得 m＝－3，n＝－2，∴A(－3，4)，B(6，－2)，‎ ‎∴k＝－3×4＝－12，‎ ‎∴反比例函数的解析式为y2＝－.‎ ‎(2)S△AOB＝S△AOC＋S△BOC ‎＝×3×4＋×3×2＝9.‎ ‎(3)由图象可知，当x＜0时，‎ 不等式ax＋b＞的解集为x＜－3.‎ ‎25．(14分)在△ABC中，∠ACB＝45°.点D(与点B，C不重合)为射线BC上一动点，连接AD，以AD为一边且在AD的右侧作正方形ADEF.‎ ‎(1)如果AB＝AC，如图①，且点D在线段BC上运动．试判断线段CF与BD之间的位置关系，并证明你的结论；‎ ‎(2)如果AB≠AC，如图②，且点D在线段BC上运动．(1)中结论是否成立，为什么？‎ ‎(3)若正方形ADEF的边DE所在直线与线段CF所在直线相交于点P，设AC＝4，BC＝3，CD＝x，求线段CP的长(用含x 的式子表示).‎ ‎　　‎ 解：(1)CF与BD之间的位置关系是垂直．‎ 证明：∵AB＝AC，∠ACB＝45°，‎ ‎∴∠ABC＝45°.‎ 由正方形ADEF得AD＝AF，‎ ‎∵∠DAF＝∠BAC＝90°，‎ ‎∴∠DAB＝∠FAC，∴△DAB≌△FAC(SAS)，∴∠ACF＝∠ABD.‎ ‎∴∠BCF＝∠ACB＋∠ACF＝90°.‎ 即CF⊥BD.‎ ‎(2)AB≠AC时，(1)中结论成立．理由略．‎ ‎(3)过点A作AQ⊥BC交CB的延长线于点Q，‎ ‎①点D在线段BC上运动时，如答图(3)①，‎ ‎∵∠BCA＝45°，可求出AQ＝CQ＝4.‎ ‎∴DQ＝4－x，△AQD∽△DCP，‎ ‎∴＝，∴＝，∴CP＝－＋x.‎ 答图(3)①‎ ‎　　答图(3)②‎ ‎②点D在BC延长线上运动时，如答图(3)②，‎ ‎∵∠BCA＝45°，∴AQ＝CQ＝4，‎ ‎∴DQ＝4＋x.同理可证△AQD∽△DCP，‎ ‎∴＝，∴＝，∴CP＝＋x.‎ ‎∴综上所述，线段CP的长为或.‎