- 2021-11-06 发布 |
- 37.5 KB |
- 9页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2019九年级数学上册 专题突破讲练 构造相似三角形解题试题 (新版)青岛版
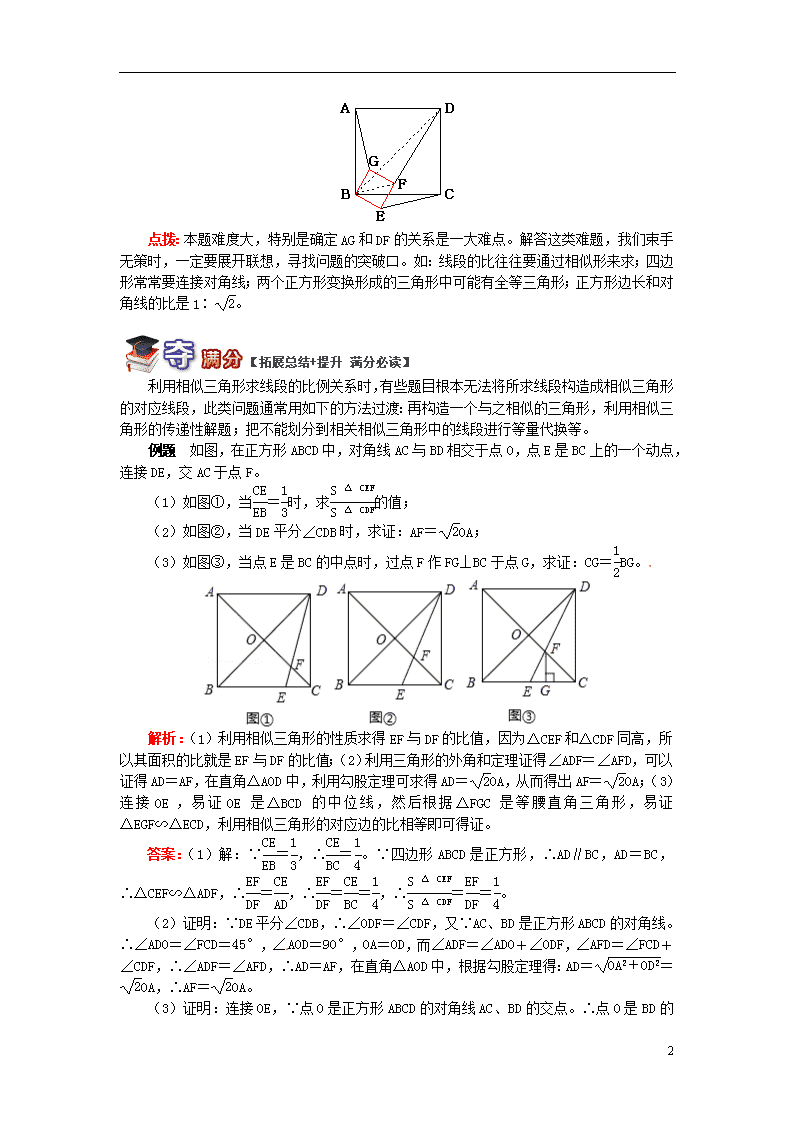
构造相似三角形解题 构造相似三角形的基本方法 1. 由平行得相似,如图①和②; 2. 由同角或等角得相似,如图③; 3. 由垂直得相似,如图④。 方法归纳:在较为复杂的图形中,我们一般通过特殊图形(如等腰三角形、平行四边形、圆等)的边或角构造相似三角形,如需添加辅助线,应考虑添加辅助线后能构成相等的角或比例线段,如:过中点(或等分点)作平行线,过某点作平行或垂直等。 总结: 1. 学会构造相似三角形的方法和技巧,能熟练地将边和角划分到相关的相似三角形中。 2. 能够综合运用相似三角形的判定和性质解决较为复杂的问题。 例题 如图所示,四边形ABCD和BEFG均为正方形,则AG∶DF∶CE=( ) A. 1∶1∶1 B. 1∶2∶1 C. 1∶∶ D. 1∶∶1 解析:不难证明△ABG≌△CBE,所以AG=CE。那么,本题只要求AG∶DF即可。要求AG和DF的比需要构造一个含有这两条线段的相似三角形,并且这对相似三角形的相似比要能求出来。在正方形中,边长和对角线的比是可求的,所以本题可试着连接BF和BD,通过三角形相似来求解。 答案:连接BF、BD。因为∠ABG=∠ABE-∠EBG=∠ABE-90°,∠CBE=∠ABE-∠ABC=∠ABE-90°。所以∠ABG=∠CBE,又AB=BC,BG=BE,所以△ABG≌△CBE,所以AG=CE。因为∠DBF=∠ABE-∠ABD-∠EBF=∠ABE-45°-45°=∠ABE-90°,所以∠DBF=∠ABG。又因为所有正方形都相似,所以这两个正方形的对角线的比BD∶BF、边长的比AB∶BG,都等于这两个正方形的相似比,即BD∶BF=AB∶BG,所以AB∶BD=BG∶BF,所以△ABG∽△DBF。所以AG∶DF=BG∶BF=1∶。所以AG∶DF∶CE=1∶∶1。故选D。 9 点拨:本题难度大,特别是确定AG和DF的关系是一大难点。解答这类难题,我们束手无策时,一定要展开联想,寻找问题的突破口。如:线段的比往往要通过相似形来求;四边形常常要连接对角线;两个正方形变换形成的三角形中可能有全等三角形;正方形边长和对角线的比是1∶。 利用相似三角形求线段的比例关系时,有些题目根本无法将所求线段构造成相似三角形的对应线段,此类问题通常用如下的方法过渡:再构造一个与之相似的三角形,利用相似三角形的传递性解题;把不能划分到相关相似三角形中的线段进行等量代换等。 例题 如图,在正方形ABCD中,对角线AC与BD相交于点O,点E是BC上的一个动点,连接DE,交AC于点F。 (1)如图①,当=时,求的值; (2)如图②,当DE平分∠CDB时,求证:AF=OA; (3)如图③,当点E是BC的中点时,过点F作FG⊥BC于点G,求证:CG=BG。 解析:(1)利用相似三角形的性质求得EF与DF的比值,因为△CEF和△CDF同高,所以其面积的比就是EF与DF的比值;(2)利用三角形的外角和定理证得∠ADF=∠AFD,可以证得AD=AF,在直角△AOD中,利用勾股定理可求得AD=OA,从而得出AF=OA;(3)连接OE,易证OE是△BCD的中位线,然后根据△FGC是等腰直角三角形,易证△EGF∽△ECD,利用相似三角形的对应边的比相等即可得证。 答案:(1)解:∵=,∴=。∵四边形ABCD是正方形,∴AD∥BC,AD=BC,∴△CEF∽△ADF,∴=,∴==,∴==。 (2)证明:∵DE平分∠CDB,∴∠ODF=∠CDF,又∵AC、BD是正方形ABCD的对角线。∴∠ADO=∠FCD=45°,∠AOD=90°,OA=OD,而∠ADF=∠ADO+∠ODF,∠AFD=∠FCD+∠CDF,∴∠ADF=∠AFD,∴AD=AF,在直角△AOD中,根据勾股定理得:AD==OA,∴AF=OA。 (3)证明:连接OE, 9 ∵点O是正方形ABCD的对角线AC、BD的交点。∴点O是BD的中点。又∵点E是BC的中点,∴OE是△BCD的中位线,∴OE∥CD,OE=CD,∴△OFE∽△CFD。∴==,∴=。又∵FG⊥BC,CD⊥BC,∴FG∥CD,∴△EGF∽△ECD,∴==。在直角△FGC中,∵∠GCF=45°,∴CG=GF,又∵CD=BC,∴==,∴=。∴CG=BG。 点拨:本题是勾股定理、三角形的中位线定理,以及相似三角形的判定与性质的综合应用,理解正方形的性质是关键。 (答题时间:45分钟) 一、选择题 *1. 如图所示,已知AD∥EF∥BC,若AD∶EF∶BC=1∶2∶4,则梯形AEFD与梯形EBCF的面积之比为( ) A. 1∶2 B. 1∶3 C. 1∶4 D. 2∶3 *2. 如图,正方形ABCD的边长为1,M、N为BD所在直线上的两点,且AM=,∠MAN=135°,则四边形AMCN的面积为( ) A. B. 2 C. D. 3 **3. 如图所示,已知在平行四边形ABCD中,M、N为AB的三等分点,DM、DN交AC于P、Q两点,则AP∶PQ∶QC=( ) A. 1∶1∶3 B. 3∶2∶5 C. 5∶3∶12 D. 5∶4∶10 9 **4. 如图所示,四边形ABCD是一个矩形,AD=12、AB=5,P是AD上任意一点,PE⊥BD于点E,PF⊥AC于点F。则PE+PF=( ) A. B. C. 5 D. 二、填空题 5. 如图,在等边△ABC中,D为BC边上一点,E为AC边上一点,且∠ADE=60°,BD=3,CE=2,则△ABC的边长为__________。 *6. 如图,在△ABC中,AB=AC=13,BC=10,D是AB的中点,过点D作DE⊥AC于点E,则DE的长是______________。 *7. 如图,△ABC中,AB=9,AC=6,点E在AB上且AE=3,点F在AC上,连接EF,若△AEF与△ABC相似,则AF=__________。 **8. 如图所示,点C在线段BG上且四边形ABCD是正方形,AG与BD、CD分别相交于点E、F,如果AE=5且EF=3,那么FG=__________。 9 三、解答题 9. 如图所示,在△ABC中,AB=AC,D是△ABC的外接圆的上任一点,连接AD、BD。求证:=。 *10. 如图所示,△ABC中,AD平分∠BAC,AD的垂直平分线FE交BC的延长线于点E。求证:DE2=BE·CE。 **11. 如图所示,在△ABC中,∠BAC=90°,AD⊥BC,E是AC的中点,ED交AB的延长线于点F。求证:=。 **12. 如图所示,F为正方形ABCD的边AB的中点,E为AD上的一点,AE=AD,FG⊥CE于点G。求证:FG2=EG·CG。 9 9 1. C 解析:延长BA、CD交于点O,则△OAD∽△OEF∽△OBC,设S△OAD=s,则S△OEF=4s,S△OBC=16s,所以S梯形AEFD∶S梯形EBCF=3S∶12S=1∶4。 2. C 解析:过点A作AE⊥BD于点E,则点E是BD中点。在Rt△AEM中,AM=,AE=,∴ME=,∴BM=。∵∠MAN=135°,∴∠MAB+∠NAD=45°,又∠AND+∠NAD=∠ADB=45°,∠AMB+∠MAB=∠ABD=45°,∴∠AND=∠MAB,∠NAD=∠AMB,∴△AND∽△MAB,∴=,即=,∴DN=。∴MN=BM+BD+DN=++=,又△AMN和△CMN面积相等,∴四边形AMCN的面积是2××MN×AE=2×××=。 3. C 解析:∵DC∥BA,∴△APM∽△CPD,∴==,∴AP=AC。同理==,∴AQ=AC。∴PQ=AC-AC=AC,又QC=AC,∴AP∶PQ∶QC=∶∶=5∶3∶12。 4. B 解析:根据题意可得AC=BD=13且△PDE∽△BDA、△PAF∽△CAD,所以=,=,即=,=,所以PD=PE,PA=PF,所以PD+PA=(PE+PF)=AD,即(PE+PF)=12,所以PE+PF=。 5. 9 解析:∵△ABC是等边三角形,∴∠BAD+∠CAD=60°。∵∠CAD+∠ADE+∠CDE+∠C=180°,∠C=60°,∠ADE=60°,∴∠CAD+∠CDE=60°。∴∠BAD=∠CDE,又∠B=∠C=60°,∴△BAD∽△CDE,∴=,设△ABC的边长为x,则=,解得x=9。 6. 解析:过点A作AG⊥BC于点G,过点B作BF⊥AC于点F。则△AGC∽△BFC,∴=。∵AB=AC,AG⊥BC,BC=10,∴BG=5,AG==12。∴=,∴BF=。∵DE⊥AC,BF⊥AC,∴DE∥BF,又点D是AB的中点,∴DE=BF=。 9 7. 2或 解析:当△AEF∽△ABC时,则=,即=,∴AF=2;当△AEF∽△ACB时,则=,AF=。∴AF=2或。 8. 解析:设正方形ABCD的边长为a,由△ADE∽△GBE得= ①;由△ADF∽△GCF得=,即= ②。由①②可得=,解得FG=。 9. 证明:∵AB=AC,∴∠ABE=∠C,∵∠D=∠C,∴∠ABE=∠D,又∵∠BAD=∠BAE,∴△ABE∽△ADB,∴=。 10. 证明:连接AE,∵EF垂直平分AD,∴AE=DE,∠FAE=∠FDE。∵∠B=∠FDE-∠BAD,∠CAE=∠FAE-∠CAD,又∠BAD=∠CAD,∴∠B=∠CAE。又∵∠AEB=∠CEA,∴△ABE∽△CAE,∴=,∴=,即DE2=BE·CE。 11. 证明:由∠BAC=90°,AD⊥BC易得△ABD∽△CBA,∴=。∵∠ABD+∠DAF=90°,∠ABD+∠C=90°,∴∠DAF=∠C。又∵点E是Rt△ADC斜边AC的中点,∴ED=EC,∴∠C=∠CDE,又∠CDE=∠BDF,∴∠BDF=∠DAF。又∠F=∠F,∴△ADF∽△DFB,∴=,∴=。 12. 证明:连接EF、CF。由AE=AD,AF=BF=AB,四边形ABCD为正方形,得==。∵∠A=∠B=90°,∴△EFA∽△FCB,∠1=∠2。∵∠2+∠3=90°,∴∠1+∠3=90°,∴∠EFC=90°。∵FG⊥CE,易证△EFG∽△FCG,∴=,∴FG2=EG·CG。 9 9查看更多