- 2022-04-02 发布 |
- 37.5 KB |
- 34页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2020年江苏省苏州市中考数学试卷
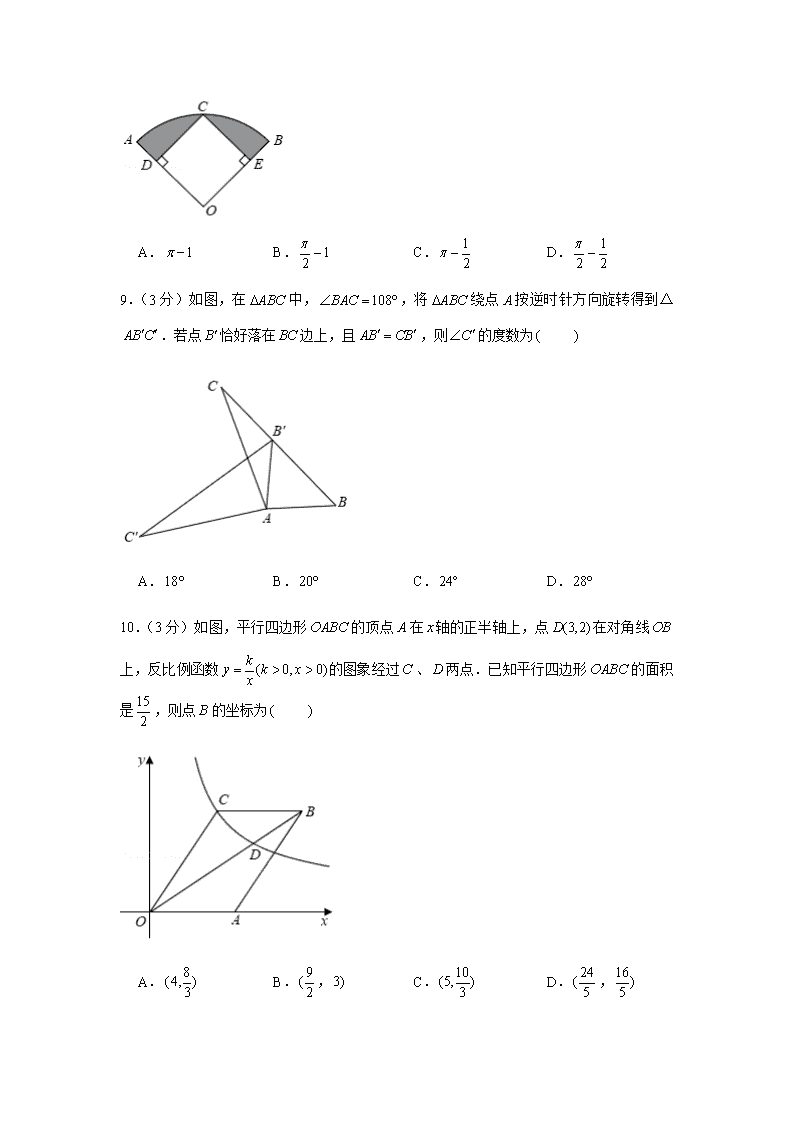
2020年江苏省苏州市中考数学试卷一、选择题:本大题共10小题,每小题3分,共30分.在每小题给出的四个选项中,只有一项是符合题目要求的.请将选择题的答案用2B铅笔涂在答题卡相应位置上.1.(3分)在下列四个实数中,最小的数是 A.B.C.0D.2.(3分)某种芯片每个探针单元的面积为,0.00000164用科学记数法可表示为 A.B.C.D.3.(3分)下列运算正确的是 A.B.C.D.4.(3分)如图,一个几何体由5个相同的小正方体搭成,该几何体的俯视图是 A.B.C.D.5.(3分)不等式的解集在数轴上表示正确的是 A.B.C.D.6.(3分)某手表厂抽查了10只手表的日走时误差,数据如下表所示(单位:日走时误差0123只数3421则这10只手表的平均日走时误差(单位:是 A.0B.0.6C.0.8D.1.17.(3分)如图,小明想要测量学校操场上旗杆的高度,他作了如下操作:(1)在点处放置测角仪,测得旗杆顶的仰角;(2)量得测角仪的高度;(3)量得测角仪到旗杆的水平距离.利用锐角三角函数解直角三角形的知识,旗杆的高度可表示为 A.B.C.D.8.(3分)如图,在扇形中,已知,,过的中点作,,垂足分别为、,则图中阴影部分的面积为 A.B.C.D.9.(3分)如图,在中,,将绕点按逆时针方向旋转得到△.若点恰好落在边上,且,则的度数为 A.B.C.D.10.(3分)如图,平行四边形的顶点在轴的正半轴上,点在对角线上,反比例函数的图象经过、两点.已知平行四边形的面积是,则点的坐标为 A.B.,C.D., 二、填空题:本大题共8小题,每小题3分,共24分.把答案直接填在答题卡相应位置上.11.(3分)使在实数范围内有意义的的取值范围是 .12.(3分)若一次函数的图象与轴交于点,则 .13.(3分)一个小球在如图所示的方格地砖上任意滚动,并随机停留在某块地砖上.每块地砖的大小、质地完全相同,那么该小球停留在黑色区域的概率是 .14.(3分)如图,已知是的直径,是的切线,连接交于点,连接.若,则的度数是 .15.(3分)若单项式与单项式是同类项,则 .16.(3分)如图,在中,已知,,垂足为,.若是的中点,则 . 17.(3分)如图,在平面直角坐标系中,点、的坐标分别为、,点在第一象限内,连接、.已知,则 .18.(3分)如图,已知是一个锐角,以点为圆心,任意长为半径画弧,分别交、于点、,再分别以点、为圆心,大于长为半径画弧,两弧交于点,画射线.过点作,交射线于点,过点作,交于点.设,,则 .三、解答题:本大题共10小题,共76分.把解答过程写在答题卡相应位置上,解答时应写出必要的计算过程、推演步骤或文字说明.作图时用2B铅笔或黑色墨水签字笔.19.(5分)计算:. 20.(5分)解方程:.21.(6分)如图,“开心”农场准备用的护栏围成一块靠墙的矩形花园,设矩形花园的长为,宽为.(1)当时,求的值;(2)受场地条件的限制,的取值范围为,求的取值范围.22.(6分)为增强学生垃圾分类意识,推动垃圾分类进校园.某初中学校组织全校1200名学生参加了“垃圾分类知识竞赛”,为了解学生的答题情况,学校考虑采用简单随机抽样的方法抽取部分学生的成绩进行调查分析.(1)学校设计了以下三种抽样调查方案:方案一:从初一、初二、初三年级中指定部分学生成绩作为样本进行调查分析;方案二:从初一、初二年级中随机抽取部分男生成绩及在初三年级中随机抽取部分女生成绩进行调查分析;方案三:从三个年级全体学生中随机抽取部分学生成绩进行调查分析.其中抽取的样本具有代表性的方案是 .(填“方案一”、“方案二”或“方案三”(2)学校根据样本数据,绘制成下表分及以上为“优秀”,60分及以上为“及格”样本容量平均分及格率优秀率最高分最低分10093.510080 分数段统计(学生成绩记为分数段频数05253040请结合表中信息解答下列问题:①估计该校1200名学生竞赛成绩的中位数落在哪个分数段内;②估计该校1200名学生中达到“优秀”的学生总人数.23.(8分)在一个不透明的布袋中装有三个小球,小球上分别标有数字0、1、2,它们除数字外都相同.小明先从布袋中任意摸出一个小球,记下数字作为平面直角坐标系内点的横坐标,将此球放回、搅匀,再从布袋中任意摸出一个小球,记下数字作为平面直角坐标系内点的纵坐标.请用树状图或表格列出点所有可能的坐标,并求出点在坐标轴上的概率.24.(8分)如图,在矩形中,是的中点,,垂足为.(1)求证:;(2)若,,求的长.25.(8分)如图,二次函数的图象与轴正半轴交于点,平行于轴的直线与该抛物线交于、两点(点位于点左侧),与抛物线对称轴交于点.(1)求的值; (2)设、是轴上的点(点位于点左侧),四边形为平行四边形.过点、分别作轴的垂线,与抛物线交于点,、,.若,求、的值.26.(10分)问题1:如图①,在四边形中,,是上一点,,.求证:.问题2:如图②,在四边形中,,是上一点,,.求的值.27.(10分)某商店代理销售一种水果,六月份的销售利润(元与销售量之间函数关系的图象如图中折线所示.请你根据图象及这种水果的相关销售记录提供的信息,解答下列问题:(1)截止到6月9日,该商店销售这种水果一共获利多少元? (2)求图象中线段所在直线对应的函数表达式.日期销售记录6月1日库存,成本价8元,售价10元(除了促销降价,其他时间售价保持不变).6月9日从6月1日至今,一共售出.6月10、11日这两天以成本价促销,之后售价恢复到10元.6月12日补充进货,成本价8.5元.6月30日水果全部售完,一共获利1200元.28.(10分)如图,已知,是的平分线,是射线上一点,.动点从点出发,以的速度沿水平向左作匀速运动,与此同时,动点从点出发,也以的速度沿竖直向上作匀速运动.连接,交于点.经过、、三点作圆,交于点,连接、.设运动时间为,其中. (1)求的值;(2)是否存在实数,使得线段的长度最大?若存在,求出的值;若不存在,说明理由.(3)求四边形的面积. 2020年江苏省苏州市中考数学试卷参考答案与试题解析一、选择题:本大题共10小题,每小题3分,共30分.在每小题给出的四个选项中,只有一项是符合题目要求的.请将选择题的答案用2B铅笔涂在答题卡相应位置上.1.(3分)在下列四个实数中,最小的数是 A.B.C.0D.【解答】解:将,,0,在数轴上表示如图所示:于是有,故选:.2.(3分)某种芯片每个探针单元的面积为,0.00000164用科学记数法可表示为 A.B.C.D.【解答】解:,故选:.3.(3分)下列运算正确的是 A.B.C.D.【解答】解:,因此选项不符合题意;,因此选项不符合题意;;因此选项不符合题意; ,因此选项符合题意;故选:.4.(3分)如图,一个几何体由5个相同的小正方体搭成,该几何体的俯视图是 A.B.C.D.【解答】解:从上面看,是一行三个小正方形.故选:.5.(3分)不等式的解集在数轴上表示正确的是 A.B.C.D.【解答】解:移项得,,合并同类项得,,的系数化为1得,.在数轴上表示为: .故选:.6.(3分)某手表厂抽查了10只手表的日走时误差,数据如下表所示(单位:日走时误差0123只数3421则这10只手表的平均日走时误差(单位:是 A.0B.0.6C.0.8D.1.1【解答】解:,故选:.7.(3分)如图,小明想要测量学校操场上旗杆的高度,他作了如下操作:(1)在点处放置测角仪,测得旗杆顶的仰角;(2)量得测角仪的高度;(3)量得测角仪到旗杆的水平距离.利用锐角三角函数解直角三角形的知识,旗杆的高度可表示为 A.B.C.D. 【解答】解:过作于,则四边形是矩形,,,,,,,故选:.8.(3分)如图,在扇形中,已知,,过的中点作,,垂足分别为、,则图中阴影部分的面积为 A.B.C.D.【解答】解:,,,四边形是矩形, 连接,点是的中点,,,,,矩形是正方形,,,图中阴影部分的面积,故选:.9.(3分)如图,在中,,将绕点按逆时针方向旋转得到△.若点恰好落在边上,且,则的度数为 A.B.C.D.【解答】解:,,,将绕点按逆时针方向旋转得到△,,,,,,,,故选:.10.(3分)如图,平行四边形的顶点在轴的正半轴上,点在对角线上,反比例函数的图象经过、两点.已知平行四边形的面积是,则点的坐标为 A.B.,C.D., 【解答】解:反比例函数的图象经过点,,,反比例函数,设的解析式为,经过点、,,解得:,的解析式为,反比例函数经过点,设,且,四边形是平行四边形,,,点的纵坐标为,的解析式为,,,, ,,解得:,,,故选:.二、填空题:本大题共8小题,每小题3分,共24分.把答案直接填在答题卡相应位置上.11.(3分)使在实数范围内有意义的的取值范围是 .【解答】解:由题意得,,解得,,故答案为:.12.(3分)若一次函数的图象与轴交于点,则 2 .【解答】解:一次函数的图象与轴交于点,,解得,故答案为2.13.(3分)一个小球在如图所示的方格地砖上任意滚动,并随机停留在某块地砖上.每块地砖的大小、质地完全相同,那么该小球停留在黑色区域的概率是 . 【解答】解:若将每个小正方形的面积记为1,则大正方形的面积为16,其中阴影部分的面积为6,所以该小球停留在黑色区域的概率是,故答案为:.14.(3分)如图,已知是的直径,是的切线,连接交于点,连接.若,则的度数是 25 .【解答】解:是的切线,,,,,,而, ,即的度数为,故答案为:25.15.(3分)若单项式与单项式是同类项,则 4 .【解答】解:单项式与单项式是同类项,,,故答案为:4.16.(3分)如图,在中,已知,,垂足为,.若是的中点,则 1 .【解答】解:设,,,,,在中, ,,在中,,,故答案为:117.(3分)如图,在平面直角坐标系中,点、的坐标分别为、,点在第一象限内,连接、.已知,则 .【解答】解:作轴于,轴于,点、的坐标分别为、,点在第一象限内,则,,,,,,,,,,在中,,在中,, ,即,解得,故答案为.18.(3分)如图,已知是一个锐角,以点为圆心,任意长为半径画弧,分别交、于点、,再分别以点、为圆心,大于长为半径画弧,两弧交于点,画射线.过点作,交射线于点,过点作,交于点.设,,则 .【解答】解:如图,连接,过点作于.由作图可知,,, ,,,,,,四边形是平行四边形,,四边形是菱形,,,,,,,,,,,,,,.故答案为. 三、解答题:本大题共10小题,共76分.把解答过程写在答题卡相应位置上,解答时应写出必要的计算过程、推演步骤或文字说明.作图时用2B铅笔或黑色墨水签字笔.19.(5分)计算:.【解答】解:.,.20.(5分)解方程:.【解答】解:方程的两边同乘,得,解这个一元一次方程,得,经检验,是原方程的解.21.(6分)如图,“开心”农场准备用的护栏围成一块靠墙的矩形花园,设矩形花园的长为,宽为.(1)当时,求的值;(2)受场地条件的限制,的取值范围为,求的取值范围.【解答】解:(1)依题意,得:,解得:.(2),, ,解得:.答:的取值范围为.22.(6分)为增强学生垃圾分类意识,推动垃圾分类进校园.某初中学校组织全校1200名学生参加了“垃圾分类知识竞赛”,为了解学生的答题情况,学校考虑采用简单随机抽样的方法抽取部分学生的成绩进行调查分析.(1)学校设计了以下三种抽样调查方案:方案一:从初一、初二、初三年级中指定部分学生成绩作为样本进行调查分析;方案二:从初一、初二年级中随机抽取部分男生成绩及在初三年级中随机抽取部分女生成绩进行调查分析;方案三:从三个年级全体学生中随机抽取部分学生成绩进行调查分析.其中抽取的样本具有代表性的方案是 方案三 .(填“方案一”、“方案二”或“方案三”(2)学校根据样本数据,绘制成下表分及以上为“优秀”,60分及以上为“及格”样本容量平均分及格率优秀率最高分最低分10093.510080分数段统计(学生成绩记为分数段频数05253040请结合表中信息解答下列问题:①估计该校1200名学生竞赛成绩的中位数落在哪个分数段内;②估计该校1200名学生中达到“优秀”的学生总人数. 【解答】解:(1)根据抽样的代表性、普遍性和可操作性可得,方案三:从三个年级全体学生中随机抽取部分学生成绩进行调查分析,是最符合题意的.故答案为:方案三;(2)①样本100人中,成绩从小到大排列后,处在中间位置的两个数都在,因此中位数在组中;②由题意得,(人,答:该校1200名学生中达到“优秀”的有840人.23.(8分)在一个不透明的布袋中装有三个小球,小球上分别标有数字0、1、2,它们除数字外都相同.小明先从布袋中任意摸出一个小球,记下数字作为平面直角坐标系内点的横坐标,将此球放回、搅匀,再从布袋中任意摸出一个小球,记下数字作为平面直角坐标系内点的纵坐标.请用树状图或表格列出点所有可能的坐标,并求出点在坐标轴上的概率.【解答】解:用列表格法表示点所有可能的情况如下:共有9种可能出现的结果,其中点在坐标轴上有5种,(点在坐标轴上).24.(8分)如图,在矩形中,是的中点,,垂足为.(1)求证:;(2)若,,求的长. 【解答】解:(1)四边形是矩形,,,,,,,;(2)是的中点,,,,,四边形是矩形,,,,. 25.(8分)如图,二次函数的图象与轴正半轴交于点,平行于轴的直线与该抛物线交于、两点(点位于点左侧),与抛物线对称轴交于点.(1)求的值;(2)设、是轴上的点(点位于点左侧),四边形为平行四边形.过点、分别作轴的垂线,与抛物线交于点,、,.若,求、的值.【解答】解:(1)直线与抛物线的对称轴交于点,故抛物线的对称轴为,即,解得:,故抛物线的表达式为:; (2)把代入并解得或3,故点、的坐标分别为、,则,四边形为平行四边形,,故,又,,,故,.或,由,解得;由,解得.26.(10分)问题1:如图①,在四边形中,,是上一点,,.求证:.问题2:如图②,在四边形中,,是上一点,,.求的值. 【解答】证明:(1),,,,又,,,,,;(2)如图2,过点作于,过点作于,由(1)可知,,,,,,,,,,,,.27.(10分)某商店代理销售一种水果,六月份的销售利润(元与销售量之间函数关系的图象如图中折线所示.请你根据图象及这种水果的相关销售记录提供的信息,解答下列问题: (1)截止到6月9日,该商店销售这种水果一共获利多少元?(2)求图象中线段所在直线对应的函数表达式.日期销售记录6月1日库存,成本价8元,售价10元(除了促销降价,其他时间售价保持不变).6月9日从6月1日至今,一共售出.6月10、11日这两天以成本价促销,之后售价恢复到10元.6月12日补充进货,成本价8.5元.6月30日水果全部售完,一共获利1200元.【解答】解:(1)(元答:截止到6月9日,该商店销售这种水果一共获利400元;(2)设点坐标为,根据题意得: ,解这个方程,得,点坐标为,设线段所在直线对应的函数表达式为,则:,解得,线段所在直线对应的函数表达式为.28.(10分)如图,已知,是的平分线,是射线上一点,.动点从点出发,以的速度沿水平向左作匀速运动,与此同时,动点从点出发,也以的速度沿竖直向上作匀速运动.连接,交于点.经过、、三点作圆,交于点,连接、.设运动时间为,其中.(1)求的值;(2)是否存在实数,使得线段的长度最大?若存在,求出的值;若不存在,说明理由.(3)求四边形的面积.【解答】解:(1)由题意可得,,, .(2)当时,线段的长度最大.如图,过点作,垂足为,则.平分,,,.设线段的长为,则,,,,,,..当时,线段的长度最大,最大为.(3),是圆的直径. .,是等腰直角三角形..在中,.四边形的面积,,.四边形的面积为.查看更多