中考数学模拟分类汇编-新概念型问题

中考数学模拟分类汇编-新概念型问题

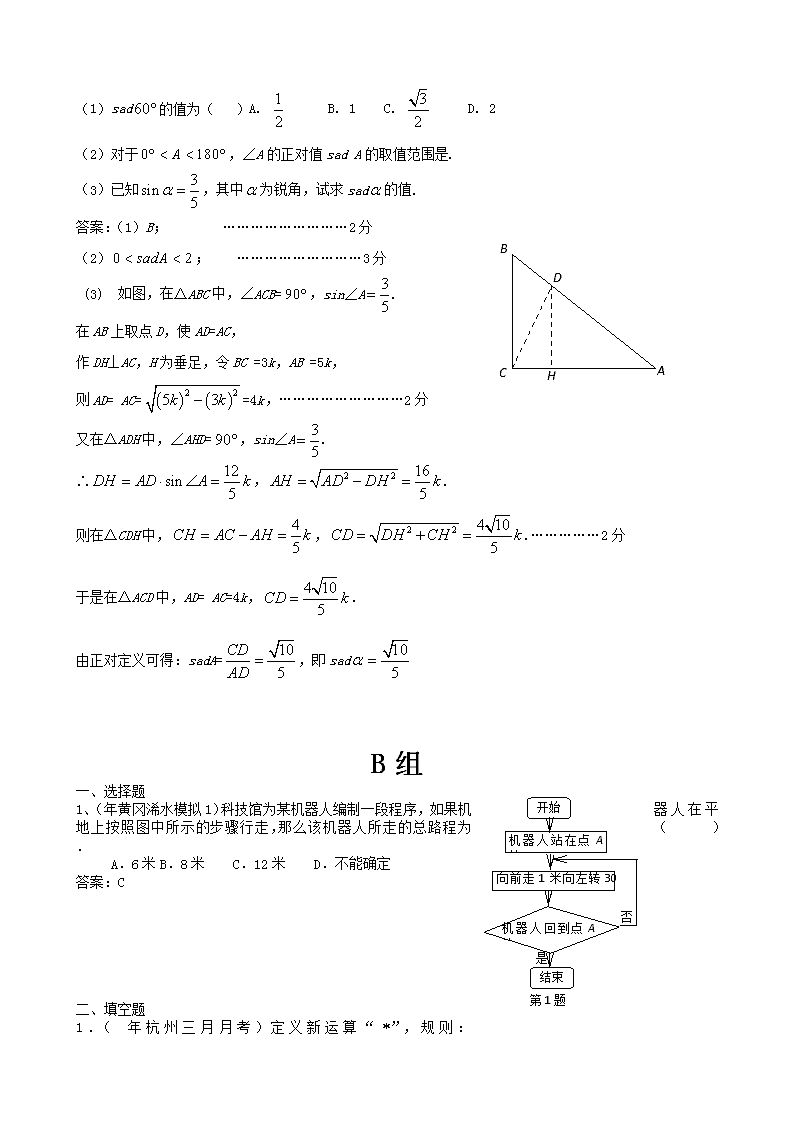
新概念型问题一、选择题1．（年浙江省杭州市中考数学模拟22)（原创）已知且满足.则称抛物线互为“友好抛物线”，则下列关于“友好抛物线”的说法不正确的是（）A、y1,y2开口方向，开口大小不一定相同B、因为y1,y2的对称轴相同C、如果y2的最值为m，则y1的最值为kmD、如果y2与x轴的两交点间距离为d，则y1与x轴的两交点间距离为答案：D二、填空题1、（年江苏盐都中考模拟）规定一种新运算a※b=a2－2b,如1※2=-3，则※（－2）=.答案62、(浙江杭州模拟16)刘谦的魔术表演风靡全国，小明也学起了刘谦发明了一个魔术盒，当任意实数对(a，b)进入其中时，会得到一个新的实数：a2＋b－1，例如把(3，－2)放入其中，就会得到：32＋（－2）－1＝6．现将实数对(－1，3)放入其中，得到实数m，再将实数对(m，1)放入其中后，得到的实数是．答案：9三、解答题1、（年北京四中中考模拟20）如图，四边形ABCD中，AB=AD，CB=CD，但ADCD，我们称这样的四边形为“半菱形”。小明说“‘半菱形’的面积等于两条对角线乘积的一半”。他的说法正确吗？请你判断并证明你的结论。解：正确。证明如下：ABCDO方法一：设AC，BD交于O，∵AB=AD，BC=DC，AC=AC，∴△ABC≌△ADE， ∴∠BAC=∠DACAB=AD，∴AO⊥BD，方法二：∵AB=AD，∴点A在线段BD的中垂线上。又∵CB=CD，∴点C与在线段BD的中垂线上，∴AC所在的直线是线段BD的中垂线，即BD⊥AC；设AC，BD交于O，∵，2、（年北京四中中考模拟18）已知：△ABC中，AB＝10⑴如图①，若点D、E分别是AC、BC边的中点，求DE的长；⑵如图②，若点A1、A2把AC边三等分，过A1、A2作AB边的平行线，分别交BC边于点B1、B2，求A1B1＋A2B2的值；⑶如图③，若点A1、A2、…、A10把AC边十一等分，过各点作AB边的平行线，分别交BC边于点B1、B2、…、B10。根据你所发现的规律，直接写出A1B1＋A2B2＋…＋A10B10的结果。解：⑴DE=5⑵A1B1＋A2B2=10⑶A1B1＋A2B2＋…＋A10B10=503、(浙江杭州模拟14)学习过三角函数，我们知道在直角三角形中，一个锐角的大小与两条边长的比值相互唯一确定，因此边长与角的大小之间可以相互转化.类似的，可以在等腰三角形中建立边角之间的联系，我们定义：等腰三角形中底边与腰的比叫做顶角的正对（sad）.如图，在△ABC中，AB=AC，顶角A的正对记作sadA，这时sadA=.容易知道一个角的大小与这个角的正对值也是相互唯一确定的.BCA根据上述对角的正对定义，解下列问题： （1）sad的值为（）A.B.1C.D.2（2）对于，∠A的正对值sadA的取值范围是.（3）已知，其中为锐角，试求sad的值.答案：BCDHA（1）B；………………………2分（2）；………………………3分(3)如图，在△ABC中，∠ACB=，sin∠A.在AB上取点D，使AD=AC，作DH⊥AC，H为垂足，令BC=3k，AB=5k，则AD=AC==4k，………………………2分又在△ADH中，∠AHD=，sin∠A.∴，.则在△CDH中，，.……………2分于是在△ACD中，AD=AC=4k，.由正对定义可得：sadA=，即sadB组第1题开始机器人站在点A处向前走1米向左转30°机器人回到点A处结束是否一、选择题1、（年黄冈浠水模拟1）科技馆为某机器人编制一段程序，如果机器人在平地上按照图中所示的步骤行走，那么该机器人所走的总路程为（）．A．6米B．8米C．12米D．不能确定答案：C二、填空题1．（年杭州三月月考）定义新运算“”，规则： ，如，。若的两根为，则＝▲．答案：2.（浙江慈吉模拟）如图是某种计算机的程序示意图,初始端输入后经“运算中心式子”(是常数,且,)处理后得到一个结果.若这个结果大于0,则输出此结果;否则就将第一次得到的结果作为输入的再次运行程序……直到输出结果为止.若该程序满足条件：“存在实数，当输入的值等于时,该程序的运算无法停止(即会一直循环运行)”，请写出一个符合条件的运算中心式子以及相应的能使它一直循环运行的的值__▲____，____▲_____.答案：说明：只需使方程有一个负数根即可；如，3．（安徽中考模拟）在数学中，为了简便，记＝1+2+3+…+(n－1)+n．1！＝1，2！＝2×1，3！＝3×2×1，…，n！＝n×(n－1)×(n－2)×…×3×2×1．则－+=．答案：04.（杭州市模拟）．如图是瑞典人科赫（Koch）在1906年构造的能够描述雪花形状的科赫雪花图案．图形的作法是，从一个正三角形开始，把每条边分成三等份，然后以各边的中间长度为底边．分别向外作正三角形，再把“底边”线段抹掉．反复进行这一过程，就会得到一个“雪花”样子的曲线．这是一个极有特色的图形：在图形不断变换的过程中，它的周长趋于无穷大，而其面积却趋于定值．如果假定原正三角形边长为，则可算出下图每步变换后科赫雪花的周长：=3，=，=，…，则=．（第15题图） 答案：=；=；=，（1+1+2分）5.（深圳市三模）在数学中，为了简便，记＝1+2+3+…+(n－1)+n.1！＝1，2！＝2×1，3！＝3×2×1，…，n！＝n×(n－1)×(n－2)×…×3×2×1.则－+＝＿＿＿.答案：0.6、（杭州模拟20）定义新运算“”，规则：，如，。若的两根为，则＝．答案：7.（浙江杭州进化一模）（本小题满分10分）学习过三角函数，我们知道在直角三角形中，一个锐角的大小与两条边长的比值相互唯一确定，因此边长与角的大小之间可以相互转化.类似的，可以在等腰三角形中建立边角之间的联系，我们定义：等腰三角形中底边与腰的比叫做顶角的正对（sad）.如图，在△ABC中，AB=AC，顶角A的正对记作sadA，这时sadA=.容易知道一个角的大小与这个角的正对值也是相互唯一确定的.BCA根据上述对角的正对定义，解下列问题：（1）sad的值为（）A.B.1C.D.2（2）对于，∠A的正对值sadA的取值范围是.（3）已知，其中为锐角，试求sad的值.答案：BCDHA（1）B；（2）；(3)如图，在△ABC中，∠ACB=，sin∠A.在AB上取点D，使AD=AC，作DH⊥AC，H为垂足，令BC=3k，AB=5k，则AD=AC==4k，又在△ADH中，∠AHD=，sin∠A.∴，.则在△CDH中，，.……………2分于是在△ACD中，AD=AC=4k，. 由正对定义可得：sadA=，即sad………………………1分8.（年杭州市模拟）（本题10分）如图①，将一张直角三角形纸片折叠，使点与点重合，这时为折痕，为等腰三角形；再继续将纸片沿的对称轴折叠，这时得到了两个完全重合的矩形（其中一个是原直角三角形的内接矩形，另一个是拼合成的无缝隙、无重叠的矩形），我们称这样两个矩形为“叠加矩形”.第23题图①图②图③第23题第23题（1）如图②，正方形网格中的能折叠成“叠加矩形”吗？如果能，请在图②中画出折痕；（2）如图③，在正方形网格中，以给定的为一边，画出一个斜三角形，使其顶点在格点上，且折成的“叠加矩形”为正方形；（3）若一个三角形所折成的“叠加矩形”为正方形，那么它必须满足的条件是什么？答案：（1）（2）图②图③（说明：只需画出折痕.）（说明：只需画出满足条件的一个三角形；答案不惟一，所画三角形的一边长与该边上的高相等即可.）（3）三角形的一边长与该边上的高相等的直角三角形或锐角三角形.