中考数学模拟分类汇编-综合型问题

中考数学模拟分类汇编-综合型问题

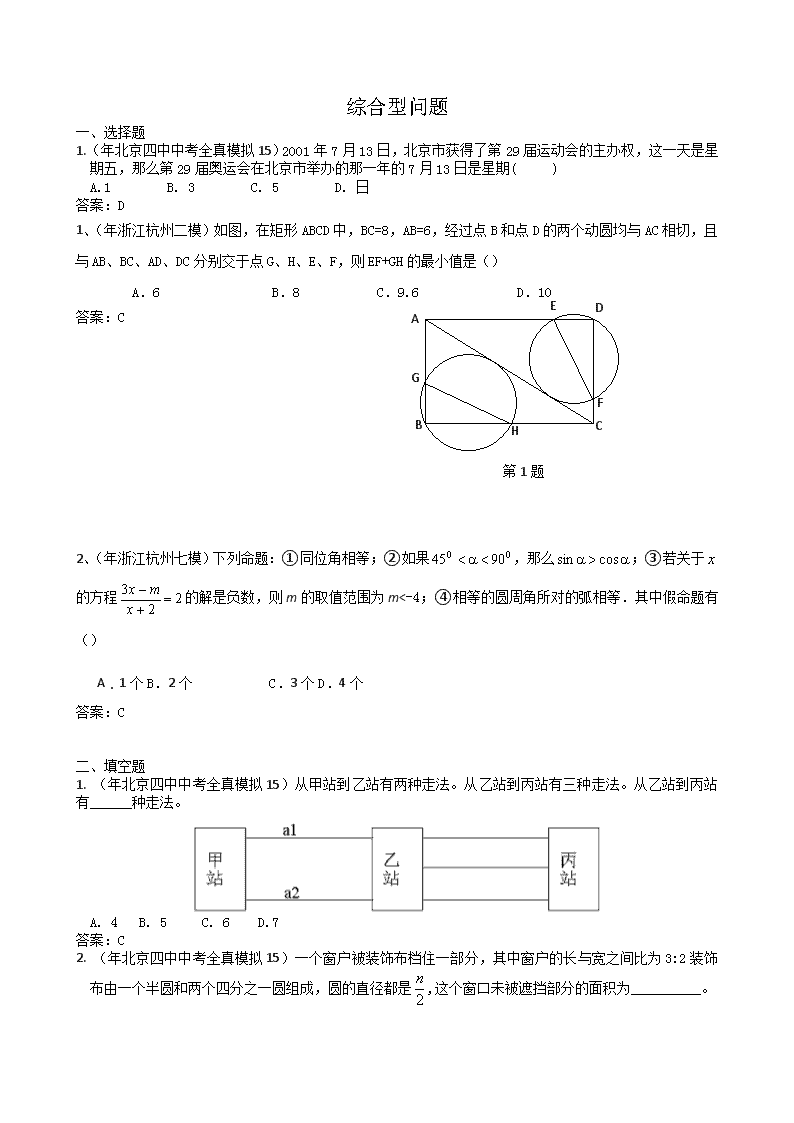
综合型问题一、选择题1.（年北京四中中考全真模拟15）2001年7月13日，北京市获得了第29届运动会的主办权，这一天是星期五，那么第29届奥运会在北京市举办的那一年的7月13日是星期()A.1B.3C.5D.日答案：D1、（年浙江杭州二模）如图，在矩形ABCD中，BC=8，AB=6，经过点B和点D的两个动圆均与AC相切，且与AB、BC、AD、DC分别交于点G、H、E、F，则EF+GH的最小值是（）AGBHCFDE第1题A．6B．8C．9.6D．10答案：C2、（年浙江杭州七模）下列命题：①同位角相等；②如果，那么；③若关于的方程的解是负数，则m的取值范围为m<-4；④相等的圆周角所对的弧相等．其中假命题有（）A．1个B．2个C．3个D．4个答案：C二、填空题1.（年北京四中中考全真模拟15）从甲站到乙站有两种走法。从乙站到丙站有三种走法。从乙站到丙站有______种走法。A.4B.5C.6D.7答案：C2.（年北京四中中考全真模拟15）一个窗户被装饰布档住一部分，其中窗户的长与宽之间比为3:2装饰布由一个半圆和两个四分之一圆组成，圆的直径都是,这个窗口未被遮挡部分的面积为__________。 答案：3.（年北京四中中考全真模拟16）如图所示，图中共有条线段，共有个长方形。毛答案：18，9．4.（年北京四中中考全真模拟17）如图，要给这个长、宽、高分别为x、y、z的箱子打包，其打包方式如右图所示，则打包带的长至少要_________（单位：mm）(用含x、y、z的代数式表示)答案：2x+4y+6z1、（年浙江杭州八模）已知正整数a满足不等式组（为未知数）无解，则函数图象与轴的坐标为答案：三、解答题1、（年江苏盐都中考模拟）（本题12分）已知：如图，在平面直角坐标系中，四边形ABCO是菱形，且∠AOC=60°，点B的坐标是（0,8），点P从点C开始以每秒1个单位长度的速度在线段CB上向点B移动，同时，点Q从点O开始以每秒a(1≤a≤3)个单位长度的速度沿射线OA方向移动，设t(0”、“=”、“<”）；（II）如图③所示，将矩形纸片ABCD放在直角坐标系中，按上述步骤一、二进行操作：（i）当点P在A点时，PT与MN交于点，点的坐标是（，）；（ii）当PA=6厘米时，PT与MN交于点，点的坐标是（，）；（iii）当PA=厘米时，在图③中用尺规作出MN（不要求写作法，要求保留作图痕迹），PT与MN交于点，点的坐标是（，）．备用图备用图解：（I）无论点P在AB边上任何位置，都有PQ=QE（填“>”、“=”、“<”）；（II）如图③所示，将矩形纸片ABCD放在直角坐标系中，按上述步骤一、二进行操作：（i）当点P在A点时，PT与MN交于点，点的坐标是（０，３）；（ii）当PA=6厘米时，PT与MN交于点，点的坐标是（６，６）；（iii）当PA=厘米时，在图③中用尺规作出MN（连结EP，做中垂线，作图略），1.（年黄冈市浠水县中考调研试题）如图，二次函数与x轴交于A、B两点，与y轴交于C点，点P从A点出发，以1个单位每秒的速度向点B运动，点Q同时从C点出发，以相同的速度向y轴正方向运动，运动时间为t秒，点P到达B点时，点Q同时停止运动。设PQ交直线AC于点G。1、求直线AC的解析式；2、设△PQC的面积为S，求S关于t的函数解析式；3、在y轴上找一点M，使△MAC和△MBC都是等腰三角形。直接写出所有满足条件的M点的坐标；4、过点P作PE⊥AC，垂足为E，当P点运动时，线段EG的长度是否发生改变，请说明理由。 答案：解：(1)(2)(3)一共四个点，(0，)，(0，0)，(0，)，（0，－2）。（4）当0＜t＜2时，过G作GH⊥y轴，垂足为H。由AP＝t，可得AE＝.由可得GH＝，所以GC＝GH＝.于是，GE＝AC－AE－GC＝＝。即GE的长度不变。当2＜t≤4时，同理可证。综合得：当P点运动时，线段EG的长度不发生改变，为定值。2.（年北京四中中考全真模拟15）在“仓库世家”游戏中，游戏规则为“只要将所有木箱归位，便可过关，可以左右上下转身，推动木箱只可前进，无法后拉，按8，2，4，6可上下左右移动。数字表示8上移一格2下移一格4左移一格6右移一格（△代表木箱，☆代表木箱应到的目的地，□代表空地，代表墙壁，移动一次只动一个格）其中第一关是如图一设计。移动方案为：→4→8→2→6→6→6→8→8→8。下图为第三关，请你设计出移动方案:方案为：→ 答案：多种方式，合理即可.3.（年北京四中中考全真模拟15）为收回建路成本，更好的保养公路，设立了公路收费站，某兴趣小组对一个收费站通过车辆情况做了调查，数据如下：时间第1分钟第2分钟第3分钟第4分钟第5分钟第7分钟第8分钟第9分钟第10分钟通过车辆数242325222623242524⑴利用上述数据求平均每分钟通过多少车辆，并估计一天通过的车辆数。⑵收费站规定，一辆机动车通过一次原则上收费20元，以保护环境为根本，达到环保指标的减少1元收费，不达标的多收2元，若某天的总收入为y元，通过的达标车辆是不达标车辆的x倍，求x与y之间的函数关系式。此段公路修建花费70万元，收费站每天还要拿出100元用于修建费用，问：x为多少时，收费站能在三年内收回成本。答案：(1）（24+23+……+24）÷9=24一天：24×24×60=34560(2)(3)700000+100×3×365=x≈1.8（倍.毛4.（年北京四中中考全真模拟16）如图，某天晚8点时，一台风中心位于点O正北方向160千米点A处，台风中心以每小时20千米的速度向东南方向移动，在距台风中心小于等于120千米的范围内将受到台风影响，同时在点O有一辆汽车以每小时40千米的速度向东行驶。（1）汽车行驶了多少时间后受到台风的影响？（2）汽车受到台风影响的时间有多少？答案：解：（1）设经过t小时后汽车受到了台风的影响，此时汽车行驶到了点B，台风中心移到点C，则OB=40t,AC=20t，作CP⊥OB于点P，CQ⊥OA于点Q，则AQ=20t,CQ=20t,所以BP=OB-OP=OB-CQ=20t,CP=OQ=OA-AQ=160-20t,由BP2+CP2=BC2，得（20t）2+(160-20t)2=1202,化简得t2-8t+14=0,解得t1=4-,t2=4+,所以，经过4-小时后，汽车受到台风影响。 （2）当t1≤t≤t2时，（20t）2+(160-20t)2≤1202，所以在t1到t2这段时间内，汽车一直受到台风影响，因为∣t1-t2∣=2，所以汽车受台风影响的时间为2小时。5.（年北京四中中考全真模拟16）如图，在Rt△AOB中，∠AOB=90°，OA=3cm，OB=4cm，以点O为坐标原点建立坐标系，设P、Q分别为AB、OB边上的动点它们同时分别从点A、O向B点匀速运动，速度均为1cm/秒，设P、Q移动时间为t（0≤t≤4）（1）过点P做PM⊥OA于M，求证：AM：AO=PM：BO=AP：AB，并求出P点的坐标（用t表示）（2）求△OPQ面积S（cm2），与运动时间t（秒）之间的函数关系式，当t为何值时，S有最大值？最大是多少？（3）当t为何值时，△OPQ为直角三角形？（4）证明无论t为何值时，△OPQ都不可能为正三角形。若点P运动速度不变改变Q的运动速度，使△OPQ为正三角形，求Q点运动的速度和此时t的值。答案：中考数学模拟试题（16）参考答案: 6.（年北京四中中考全真模拟17）已知:反比例函数和一次函数，其中一次函数的图像经过点（k,5）.（1）试求反比例函数的解析式；（2）若点A在第一象限，且同时在上述两函数的图像上，求A点的坐标。答案：解：（1）因为一次函数的图像经过点（k,5）所以有5＝2k-1解得k＝3所以反比例函数的解析式为y=（2）由题意得：解这个方程组得：或因为点A在第一象限，则x>0y>0，所以点A的坐标为（，2）7.（年北京四中中考全真模拟17）如图，以Rt△ABC的直角边AB为直径的半圆O，与斜边AC交于D，E是BC边上的中点，连结DE.(1)DE与半圆O相切吗？若相切，请给出证明；若不相切，请说明理由；(2)若AD、AB的长是方程x2－10x+24=0的两个根，求直角边BC的长。答案：解：（1）DE与半圆O相切.证明：连结OD、BD∵AB是半圆O的直径∴∠BDA=∠BDC=90°∵在Rt△BDC中,E是BC边上的中点∴DE=BE∴∠EBD＝∠BDE∵OB=OD∴∠OBD=∠ODB又∵∠ABC＝∠OBD+∠EBD＝90°∴∠ODB+∠EBD=90°∴DE与半圆O相切. （2）解：∵在Rt△ABC中，BD⊥AC∴Rt△ABD∽Rt△ABC∴=即AB2=AD·AC∴AC=∵AD、AB的长是方程x2－10x+24=0的两个根∴解方程x2－10x+24=0得：x1=4x2=6∵ADAC,以斜边AB所在直线为x轴,以斜边AB上的高所在直线为y轴,建立直角坐标系,若OA2+OB2=17,且线段OA、OB的长度是关于x的一元二次方程x2-mx+2(m-3)=0的两个根.（1）求C点的坐标；（2）以斜边AB为直径作圆与y轴交于另一点E，求过A、B、E三点的抛物线的解析式，并画出此抛物线的草图；（3）在抛物线上是否存在点P，使△ABP与△ABC全等？若存在，求出符合条件的P点的坐标；若不存在，说明理由.答案：解：（1）∵线段OA、OB的长度是关于x的一元二次方程x2－mx+2(m－3)=0的两个根，∴　　又　∵OA2+OB2=17，∴（OA+OB）2－2·OA·OB=17.（3）∴把（1）（2）代入（3），得m2－4(m－3)=17.∴m2－4m－5=0.，　　解得m=-1或m=5.又知OA+OB=m>0，∴m=－1应舍去.∴当m=5时，得方程x2－5x+4=0.解之，得x=1或x=4.∵BC>AC,　　∴OB>OA.∴OA=1，OB=4.在Rt△ABC中，∠ACB=90°，CO⊥AB，∴OC2=OA·OB=1×4=4.∴OC=2，　∴C（0，2）.（2）∵OA=1，OB=4，C、E两点关于x轴对称，∴A(－1,0),B(4,0),E(0,－2).设经过A、B、E三点的抛物线的解析式为y=ax2+bx+c,则∴所求抛物线解析式为（3）存在.∵点E是抛物线与圆的交点，∴Rt△ACB≌△AEB.∴E（0，-2）符合条件.∵圆心的坐标（，0）在抛物线的对称轴上，∴这个圆和这条抛物线均关于抛物线的对称轴对称.∴点E关于抛物线对称轴的对称点E′也符合题意.∴可求得E′（3，-2）.∴抛物线上存在点P符合题意，它们的坐标是（0，-2）和（3，-2）。 26.（年广东省澄海实验学校模拟）已知：如图，抛物线与轴交于点、点，与直线相交于点、点，直线与轴交于点。（1）求直线的解析式；（2）求的面积；第1题图（3）若点在线段上以每秒1个单位长度的速度从向运动（不与重合），同时，点在射线上以每秒2个单位长度的速度从向运动．设运动时间为秒，请写出的面积与的函数关系式，并求出点运动多少时间时，的面积最大，最大面积是多少？解：（1）在中，令，xyABCEMDPNO，1分又点在上…………………………………2分的解析式为………………………3分（2）过点C作CD⊥AB于点D.由，得5分，，………………………………………6分7分（3）过点作于点8分由直线可得：在中，，，则，∵BM=4－t∴△MBN的面积=×BM×NP=(4－t)·t10分11分此抛物线开口向下，当时，当点运动2秒时，的面积达到最大，最大为．12分 27.（湖北省崇阳县城关中学模拟）(本小题满分12分)ABCDGo第2题如图，在平面直角坐标系xoy中，矩形ABCD的边AB在x轴上，且AB=3，BC=，直线y=经过点C，交y轴于点G。（1）点C、D的坐标分别是C（），D（）；（2）求顶点在直线y=上且经过点C、D的抛物线的解析式；（3）将（2）中的抛物线沿直线y=平移，平移后的抛物线交y轴于点F，顶点为点E（顶点在y轴右侧）。平移后是否存在这样的抛物线，使⊿EFG为等腰三角形？若存在，请求出此时抛物线的解析式；若不存在，请说明理由。……2′解：（1）……2′（2）由二次函数对称性得顶点横坐标为，代入一次函数，得顶点坐标为（，），∴设抛物线解析式为，把点代入得，……2′∴解析式为（3）设顶点E在直线上运动的横坐标为m，则……2′∴可设解析式为①当FG=EG时，FG=EG=2m，代入解析式得：，得m=0(舍去)，，……2′此时所求的解析式为：；②当GE=EF时，FG=4m，代入解析式得：，得m=0(舍去)，，……2′此时所求的解析式为：；③当FG=FE时，不存在； 28.（深圳市模四）（2）如图，AB为⊙O的直径，BC切⊙O于B，AC交⊙O于D.①求证：AB2=AD·AC.②当点D运动到半圆AB什么位置时，△ABC为等腰直角三角形，为什么？ABCDO·第3（2）题图证明：①连接BD，则∠ADB=90°.∵BC与⊙O相切，∴∠ABC=90°，∴∠ABC=∠ADB。又∵∠A=∠A，∴△ABC∽△ADB，∴,∴.②点D运动到半圆AB的中点时，△ABC为等腰直角三角形。BD既是AC上的高线又是中线，所以△ABC为等腰直角三角形。29.（深圳市模四）、（9分）一次函数的图像与反比例函数的图像交于点M（2,3）和另外一个点N。⑴求出一次函数和反比例函数的解析式；⑵求出点N的坐标；⑶求出△MON的面积。解：（1）∵点M（2,3）在一次函数上，∴。∴一次函数。∵点M（2,3）在反比例函数上，∴m=6。反比例函数为。（2）联立两解析式得解得所以点N（－3，－2）。（3）设MN交y轴于点A，在中，令x=0，得y=1。所以点A的坐标为（0,1）。所以＝30.（湖北省崇阳县城关中学模拟）（本小题满分8分）已知正比例函数（a＜0）与反比例函数 的图象有两个公共点，其中一个公共点的纵坐标为4．（1）求这两个函数的解析式；（2）在坐标系中画出它们的图象（可不列表）；（3）利用图像直接写出当x取何值时，．……2′（1）∵交点纵坐标为4，∴，解得（舍去）……2′-24-42（2，-4）（-2，4）∴正比例函数：反比例函数：（2）……2′第5题图……2′（3）当时，31.（深圳市模四）（9分）已知，如图，直角坐标系中的等腰梯形ABCD，AB∥CD，下底AB在x轴上，D在y轴上，M为AD的中点，过O作腰BC的垂线交BC于点E.（1）求证：OM⊥OE；（2）若等腰梯形中AD所在的直线的解析式为，且，求过等腰梯形ABCD的三个顶点的抛物线的解析式。（3）若点M在梯形ABCD内沿水平方向移动到N，且使四边形MNCD为平行四边形，抛物线上是否存在一点P，使S△PAB与四边形MNCD的面积相等，若存在，求出P点的坐标；若不存在，请说明理由。第6题图解：（1）∠A=∠B，因为M为直角三角形AOD的斜边中点，所以OM=MA，则∠A=∠MOA，所以∠MOA=∠B；又OE⊥BC，所以∠B+∠BOE=90°，所以∠MOA+∠BOE=90°，则OM⊥OE；（2）可以求得D（0，4），A（-3，0）所以OA=3，OD=4，AB=8，DC=2，所以B（5，0）、C（2，4），设过A、B、D的抛物线为，将点D的坐标代入，求出a=，即，验证点C也在此抛物线上，所以所求的抛物线为； （3）可以求出N（0.5，2），所以平行四边形MNCD的面积为4，设P（m，n），又AB=8，所以，则，所以n=±1；当n=1时，，所以x=0或2；当n=-1时，，所以x=；因此这样的点P有四个，分别为（0，1）、（2，1）、（，-1）、（，-1）。32、（年北京四中33模）如图，一次函数y=kx+b的图象与反比例函数的图象交于A（－6，2）、B（4，n）两点，直线AB分别交x轴、y轴于D、C两点。（1）求上述反比例函数和一次函数的解析式；（2）若AD=tCD，求t。答案：解（1）把x=－6，y=2代入，得：m=－12∴反比例函数的解析式为把x=4，y=n代入得把x=－6，y=2，x=4，y=－3分别代入y=kx+b，得解得：∴一次函数的解析式为（2）过A作AE⊥x轴，E点为垂足，∵A点的纵坐标为2，∴AE=2E由一次函数的解析式为得C点的坐标为（0，－1）∴OC=1在Rt△COD和Rt△AED中，∠COD=∠AED=90°，∠CDO=∠ADE∴Rt△COD∽Rt△AED∴，∴t=233、（年浙江杭州27模）如图，在⊙O中，OA、OB是半径，且OA⊥OB，OA=6，点C是AB上异于A、B的动点。过点C作CD⊥OA于点D，作CE⊥OB于点E，连接DE，点G、H在线段DE上，且DG=GH=HE。（1）求证：四边形OGCH为平行四边形；OBECHGDA（2）①当点C在AB上运动时，在CD、CG、DG中，是否存在长度不变的线段？若存在，请求出该线段的长度；若不存在，请说明理由；②求CD2+CH2之值。答案：（1）证明：如右图，∵CD⊥OA，CE⊥OB，∴∠ODC=∠OEC=90°又∵∠AOB=90°，∴四边形OECD是矩形。……（1分）∴OD=EC，且OD//EC，∴∠ODG=∠CEH∵DG=EH，∴△ODG≌△CEH，∴OG=CH。 同理可证OH=CG∴四边形OGCH为平行四边形……………………（3分）（2）①解：线段DG的长度不变。…………………………………………………（4分）∵点C是AB上的点，OA=6。∴OC=OA=6∵四边形OECD是矩形，∴ED=OC=6………………………………………………（5分）∵DG=GH=HE，∴DG=ED=2………………………………………………………（6分）②解：如右图，过点H作HF⊥CD于点F，∵EC⊥CD，∴HF//EC∴△DHF∽△DEC，∴，∴……………………（7分）F从而CF=CD－FD=CD在Rt△CHF中，CH2=HF2+CF2=HF2+CD2在Rt△HFD中，HF2=DH2－DF2=CD2………………（9分）∴CH2=CD2+CD2=16－CD2∴……………………………………（11分）34、（年北京四中34模）已知：如图，内接于⊙O，为直径，弦于，是弧AD的中点，连结并延长交的延长线于点，连结，分别交、于点、．（1）求证：是的外心；（2）若⊙O的半径是，CE=16，求的长。答案：(1)∵为直径，弦，是弧AD的中点∴弧AC=弧AE=弧CD∴∠ACE=∠CAD∴CP=AP∵∠ACB=90°∴∠ACE+∠PCQ=∠CAD+∠CQP=90°∴∠PCQ=∠CQP∴CP=AP=PQ∴是的外心（2）连结CO∵CO=CF=CE=8∴OF==∴AF=6AC=10BC=5∵∠CAQ=∠ABC，∠ACQ=∠BCAF∴⊿ACQ∽⊿BCA∴ ∴得CQ=35、（年浙江杭州27模）如图，在平面直角坐标系xoy中，矩形ABCD的边AB在x轴上，且AB=3，BC=，直线y=经过点C，交y轴于点G。（1）点C、D的坐标分别是C（），D（）；（2）求顶点在直线y=上且经过点C、D的抛物线的解析式；（3）将（2）中的抛物线沿直线y=平移，平移后的抛物线ABCDGo交y轴于点F，顶点为点E。平移后是否存在这样的抛物线，使△EFG为等腰三角形？若存在，请求出此时抛物线的解析式；若不存在，请说明理由。答案：（1）C（4，），D（1，）；（2）由抛物线的顶点坐标为（）（2分）可得抛物线的解析式为（3）设抛物线沿直线y=平移后的抛物线的顶点为，则平移后抛物线的解析式为当时，若，则解得 ∴若，则解得∴若，则∠120°（不合题意，舍去）当时，∠为钝角，则当⊿EFG为等腰三角形时，∴解得，∴36、（年浙江杭州28模）如图，点P是菱形ABCD的对角线BD上一点，连结CP并延长，交AD于E，交BA的延长线于点F．试问：(1)图中△APD与哪个三角形全等？并说明理由．(2)猜想：线段PC、PE、PF之间存在什么关系？并说明理由．答案：解：(1)△APD≌△CPD1分理由：∵四边形ABCD菱形∴AD=CD,∠ADP=∠CDP又∵PD=PD∴△APD≌△CPD(2)猜想：证明：∵△APD≌△CPD∴∠DAP=∠DCP∵CD∥BF ∴∠DCP=∠F∴∠DAP=∠F又∵∠APE=∠FPA∴△APE∽△FPA∴∴∵△APD≌△CPD∴PA=PC∴37.（年杭州市模拟）（本题12分）矩形在直角坐标系中的位置如图所示，、两点的坐标分别为、，直线与边相交于点.(1)若抛物线经过、两点，试确定此抛物线的表达式；(2)若以点为圆心的⊙与直线相切，试求⊙的半径；第24题(3)设(1)中抛物线的对称轴与直线交于点，在对称轴上是否存在点，以、、为顶点的三角形与相似，若存在,试求出符合条件的点的坐标；若不存在，试说明理由.答案：（1）解得D点的坐标为D（4，3）抛物线经过D（4，3）、A（6，0），可得（2）∵CD=4，OC=3，OD=.sin∠CDO=，过A作AH⊥OD于H，则AH=OAsin∠DOA=6×==3.6，∴当直线OD与⊙A相切时，r=3.6.（3）设抛物线的对称轴与轴交于点Q，则点Q符合条件.∵CB∥OA，∴∠QOM=∠ODC，∴Rt△QOM∽Rt△CDO.∵对称轴=，∴Q点的坐标为Q（3，0）.又过O作OD的垂线交抛物线的对称轴于点Q，则点Q也符合条件.∵对称轴平行于轴，∴∠QMO=∠DOC，∴Rt△QMO∽Rt△DOC.在Rt△QQO和Rt△DCO中，QO=CO=3，∠Q=∠ODC，∴Rt△QQO≌Rt△DCO，∴CD=QQ=4，∵Q位于第四象限，∴Q（3，-4）.因此，符合条件的点有两个，分别是Q（3，0），Q（3，-4）.38．（年海宁市盐官片一模）如图，抛物线经过、两点，与 轴交于另一点．（1）求抛物线的解析式；（2）已知点在第一象限的抛物线上，求点关于直线对称的点的坐标；yxOABC（3）在（2）的条件下，连接，点为抛物线上一点，且，求点的坐标．答案：解：（1）抛物线经过，两点，解得抛物线的解析式为．yxOABCDE（2）点在抛物线上，，即，或．点在第一象限，点的坐标为．由（1）知．设点关于直线的对称点为点．，，且，，yxOABCDEPF点在轴上，且．，．即点关于直线对称的点的坐标为（0，1）．（3）作于，于．由（1）有：，．，且． ，．，，，．设，则，，．点在抛物线上，，（舍去）或，．39、（赵州二中九年七班模拟）（8分）某同学在A、B两家超市发现他看中的随身听的单价相同，书包单价也相同，随身听和书包单价之和是452元，且随身听的单价比书包单价的4倍少8元。　（1）求该同学看中的随身听和书包单价各是多少元？　（2）某一天该同学上街，恰好赶上商家促销，超市A所有商品打八折销售，超市B全场购物满100元返购物券30元销售（不足100元不返券，购物券全场通用），但他只带了400元钱，如果他只在一家超市购买看中的这两样物品，你能说明他可以选择哪一家购买吗？若两家都可以选择，在哪一家购买更省钱？BEFAOCD40、（赵州二中九年七班模拟）（12分）如图，⊙O的直径AB＝4，C、D为圆周上两点，且四边形OBCD是菱形，过点D的直线EF∥AC，交BA、BC的延长线于点E、F．(1)求证：EF是⊙O的切线；(2)求DE的长．答案：(1)证明：∵AB是⊙O的直径，∴∠ACB＝90°．∵四边形OBCD是菱形，∴OD//BC．∴∠1＝∠ACB＝90°． ∵EF∥AC，∴∠2＝∠1＝90°．∵OD是半径，∴EF是⊙O的切线．(2)解：连结OC，∵直径AB＝4，∴半径OB＝OC＝2．∵四边形OBCD是菱形，∴OD＝BC＝OB＝OC＝2．∴∠B＝60°．∵OD//BC，∴∠EOD＝∠B＝60°．在Rt△EOD中，．